この記事では曲げを受ける材料中に発生する応力(曲げ応力)の考え方を徹底的に噛み砕いて解説していきたい。
かなり長くなるが、曲げ応力のことが分からないという人は絶対タメになると思うので、ぜひ最後まで読んでみてほしい。
 材料力学 SFD/BMDって何?その意義を超詳しく解説【材力Vol. 6-1】
材料力学 SFD/BMDって何?その意義を超詳しく解説【材力Vol. 6-1】
 材料力学 絶対描けるようになるSFD/BMDの描き方を徹底解説【材力Vol. 6-2】
材料力学 絶対描けるようになるSFD/BMDの描き方を徹底解説【材力Vol. 6-2】
 材料力学 すっきり理解できる断面二次モーメントの意味【材力Vol. 6-5】
材料力学 すっきり理解できる断面二次モーメントの意味【材力Vol. 6-5】
- 曲げを受ける材料の断面には、中立面を境にして引張応力と圧縮応力が同時に働く。中立面から離れるほど大きな応力が発生する。
- 曲げ応力を求めるには、曲げモーメントと断面二次モーメントおよび中立面(図心)の位置を正確に把握することがとても重要。
曲げによる応力分布
曲げによる応力、いわゆる『曲げ応力』は引張・圧縮と比べるとだいぶ複雑だ。でもコツを掴めば決して難しくない。まずは細かい計算法とかは考えずに、おおまかなことを説明したい。
棒が曲がった様子をイメージしてみよう。下図のように棒を曲げるとき、棒の上半分と下半分で変形が逆になっていることが分かるだろうか?つまり、この曲げ方向の場合、上半分が元の長さよりも縮んでおり、下半分が元の長さよりも伸びている。さらに言えば、中心から離れて表面に近いほど変形量が大きくなっている(棒の一番下側が最も伸びている)。
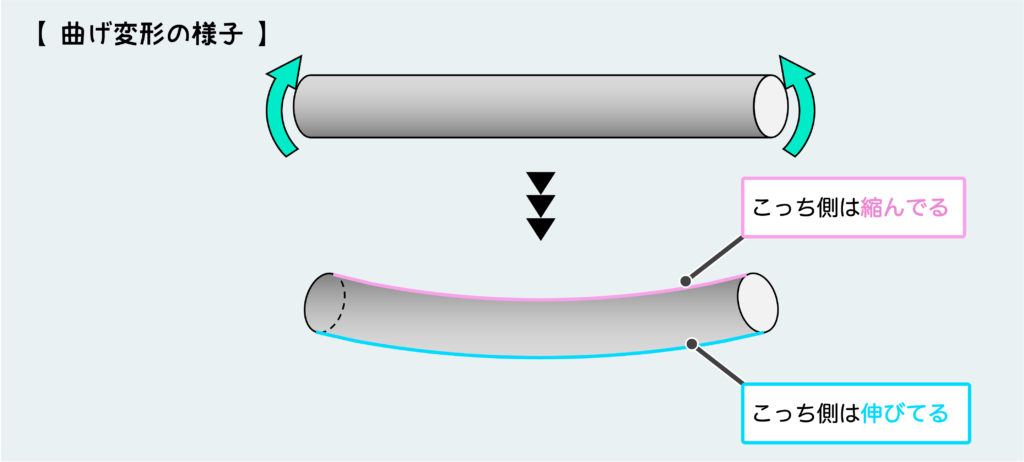
このような変形を引き起こしているのが、材料内部に働いている応力である。なので、上で書いたような変形を実現できるような応力が働く必要がある。
結論として、曲げを受ける材料のある断面上に作用する応力は下図のように描ける。
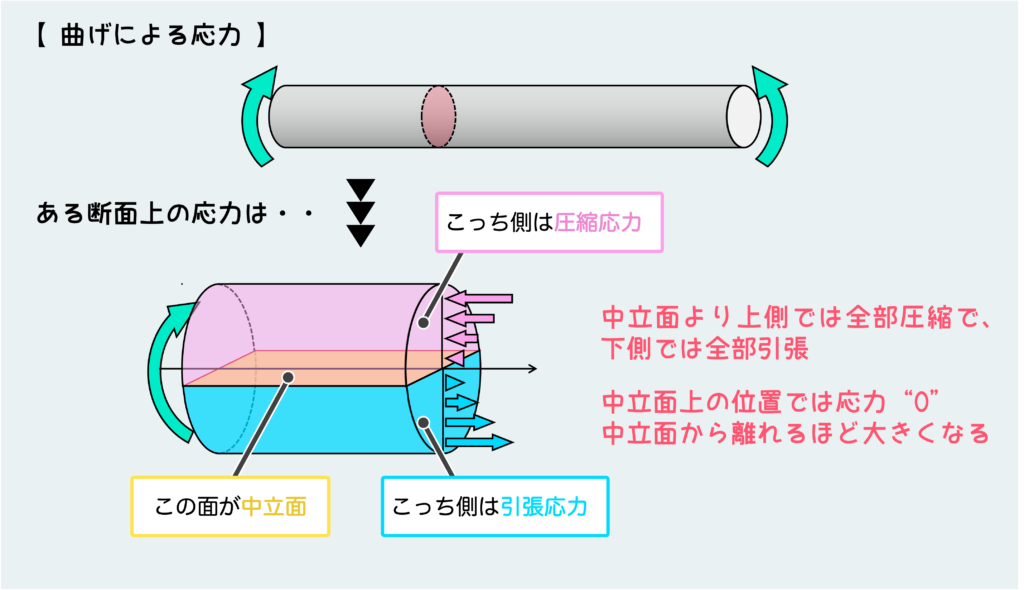
このように、曲げを受ける材料中の断面には引張応力と圧縮応力が同時に働いており、ある境界線を境目にして引張と圧縮が入れ替わる。この境界線上の位置では曲げによる垂直応力は働かず、この線から離れるほど大きくなるような応力分布を持つ。
このような曲げによる応力が働かない境界線の集まりを “中立面” と呼ぶ。
引張・圧縮でもねじりでも曲げでもどんな変形でもそうだが、応力の大きさを決めているのは『内力』だ。曲げ応力の場合、応力の大きさを決める内力は曲げモーメントである。
また、もちろん断面形状によっても応力の大きさは変わる。曲げの場合、断面形状の影響を表すパラメータが『断面二次モーメント』だ。
 材料力学 すっきり理解できる断面二次モーメントの意味【材力Vol. 6-5】
材料力学 すっきり理解できる断面二次モーメントの意味【材力Vol. 6-5】
したがって、ある断面に働く曲げ応力の分布は下のような式で表せることになる。
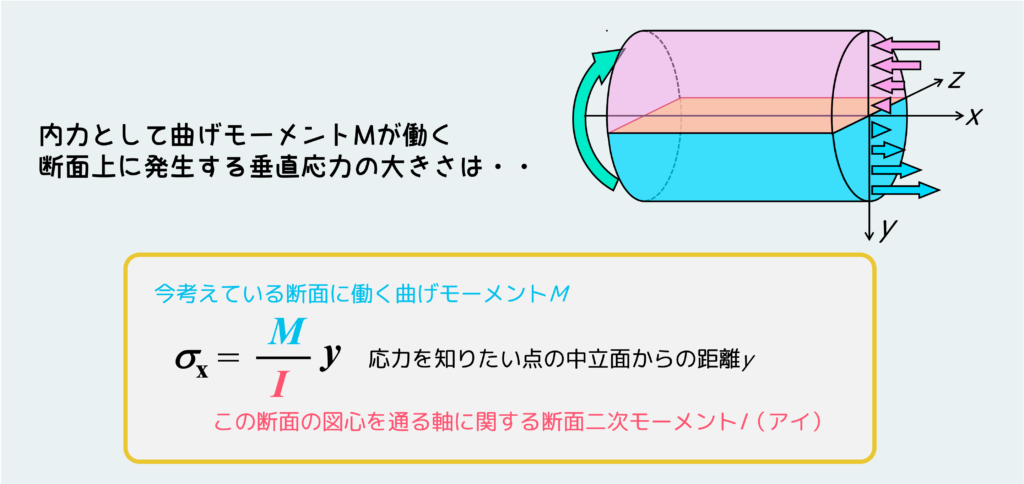
ここで、Mは今考えている断面に働く内力「曲げモーメント」の大きさである。I(アイ)はこの断面形状の図心を通る軸に関する断面二次モーメントである。最後に、yは今考えている点の中立面からの距離である。
MやIは条件が決まれば一定値に決まってしまうので、この応力分布は中立面からの距離yに比例した形になっていることが理解できると思う。y=0、すなわち中立面上の点では応力“0”であり、中立面から離れるほど応力の大きさは大きくなる。
断面上のある任意の点の応力を知りたければ、この式のyにその点の中立面からの距離を代入すればよい。
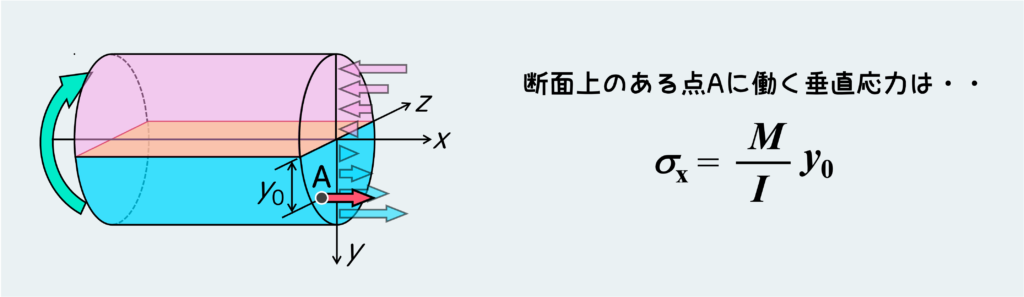
この断面上に発生する最大の垂直応力は、yのところに中立面から最も離れた(引張側の)点の距離を入れればよい。
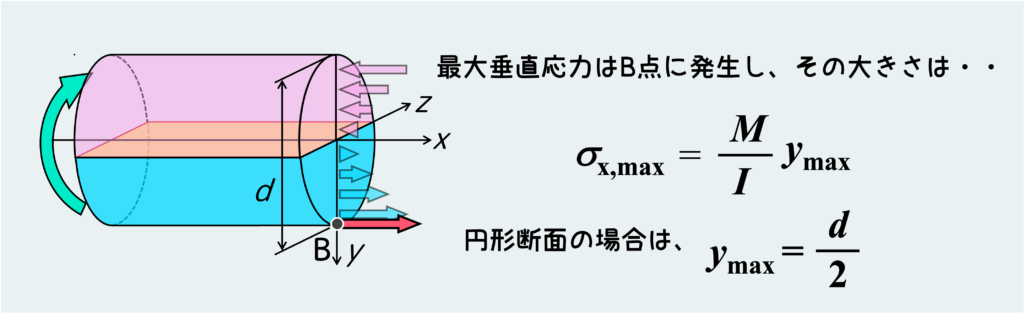
このように割と簡単な式で曲げ応力を表現することができる。式を見て一目瞭然なように、正しく曲げ応力を求めるためには無論『曲げモーメント』と『断面二次モーメント』、さらには中立面の位置を正しく把握することがすごく重要だ。
ではこれを踏まえた上で、曲げ応力を求める流れを見てみよう。
曲げの場合、応力は場所によって変わる。材料中のどこか?断面上のどこか?あるいは、場所は分からないけど最大の曲げ応力が知りたいのか?
自分が今からどこの応力を求めようとしているのか、しっかり認識しよう。
断面図形の図心を元に、応力分布の中心(引張と圧縮の境目)が決まる。また、断面形状によって断面二次モーメントが変わり、これに応じて応力分布の大きさが決まる。なので、断面図形の図心がどこに来るか見極めること、正しい断面二次モーメントを導き出すことが重要になる。
どの位置の応力を知りたいのか認識したら、その位置(断面)に働く曲げモーメントを求めよう。
材料中に働く曲げモーメントは場所によって変化していくので、BMDの考え方を使って、いま応力を知りたい場所に働いている曲げモーメントを決定しよう。
曲げモーメントと断面二次モーメントおよび図心の位置を元に、この断面上に働く応力の分布の全体像を把握しよう。図心を境にして、どっちが引張でどっちが圧縮かを判断するときは曲げモーメントの向きから変形の様子をイメージすると分かりやすい。
手順はこの通りだ。
以下では、応力を求めていく上での注意点やキーポイントについて詳しく説明したい。
中立面(図心)の位置に注意!
上の手順STEP.2で書いたが、断面図形の図心を意識することが曲げ問題においてはとっても重要だ。なぜなら、図心を元に、中立面の配置が決まるからだ。
上でも書いたように中立面というのは曲げによる応力が働かない位置の集合体である。ある断面の上に働く応力を考えたときに、この中立面が通る位置では応力は働かないし、中立面を境に引張と圧縮が入れ替わることになる。
下の図を見てもらえば分かるように、中立面は断面図形の図心を通るように位置し、曲げの方向によって配置が決定する。
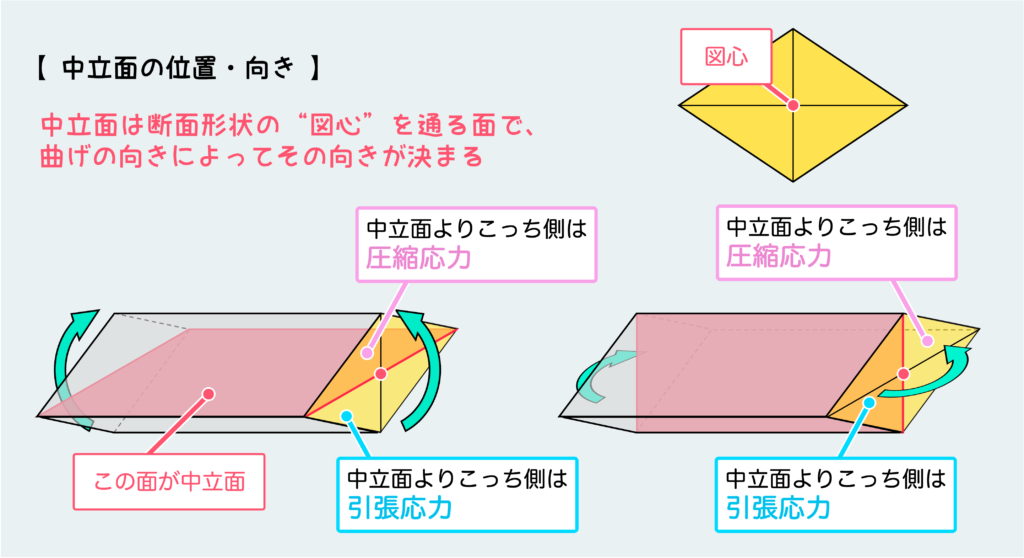
このように、中立面の位置を境にして引張と圧縮が入れ替わるし、中立面からの距離に応じて応力の大きさが決まる(中立面から距離に比例して応力が大きくなる)ので、中立面が断面上のどこに来るのか(つまりは図心がどこに来るのか)を意識・理解することは極めて重要なことなのだ。

え?縦方向に曲げるんなら、断面を上と下に半分ずつ分けて考えればいいんじゃないの?

その考え方は危険だよ!
単純に断面を半分ずつ(縦方向に曲げるなら上半分と下半分)に分けて、どっちかが引張でどっちかが圧縮って考えるのは極めて危険だ。この考え方で正しく中立面の位置(図心の位置)を決めることができるのは上下対称な図形のときだけだ。
一つずつ見ていこう。
まず断面形状がシンプル、つまり丸、四角、三角のときを確認しよう。それぞれの形状において図心の位置は下のようになる。
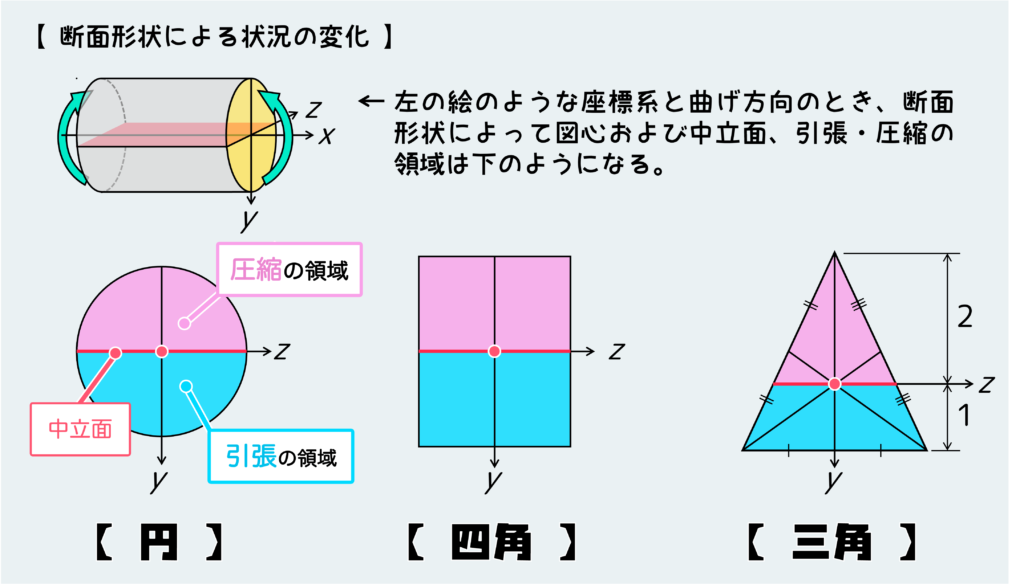
三角形断面の場合を見るとよく分かると思うが、図のような縦方向の曲げに対して必ずしも上下中央位置に図心および中立面が来る訳ではない。
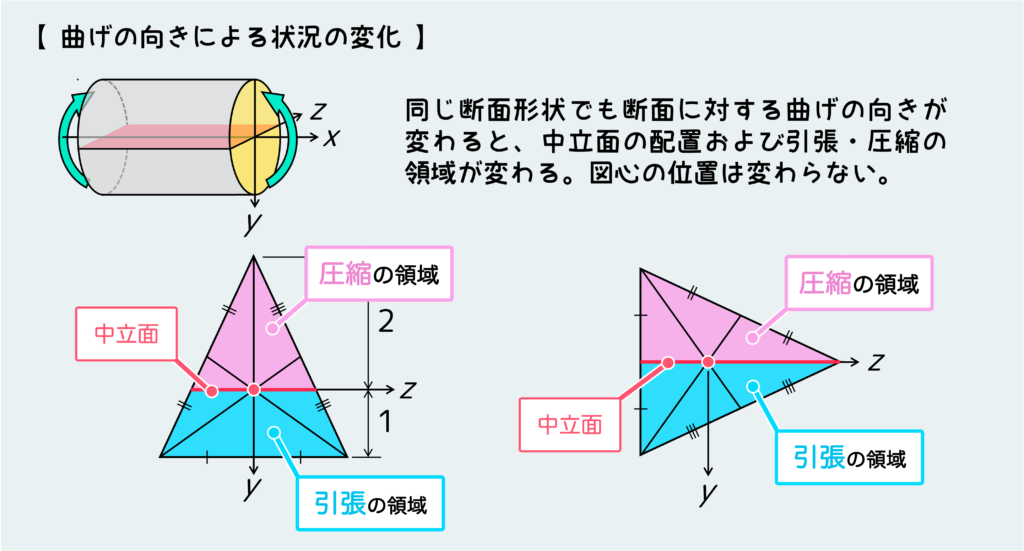
また、曲げる方向によって図心の位置は変わらないが、中立面の配置は変わるのでこれにも注意しよう。これも三角形断面の場合を見るとよく理解できると思う。
もっと複雑な形状の場合はどうなるだろうか?グニャグニャ曲がったようなヘンテコな形状だったら正直手計算はムリだと思うが、基本的に機械加工で製造するような部材であれば、どんな複雑な断面形状でもシンプルな図形(丸・四角・三角)の組合せとして考えることができる。
では、シンプルな図形の組合せで表せるような断面形状について、図心の位置の見極め方を説明しよう。
たとえば下のような断面形状を持つはりを曲げる場合に、この断面図形の図心の位置を考えよう。
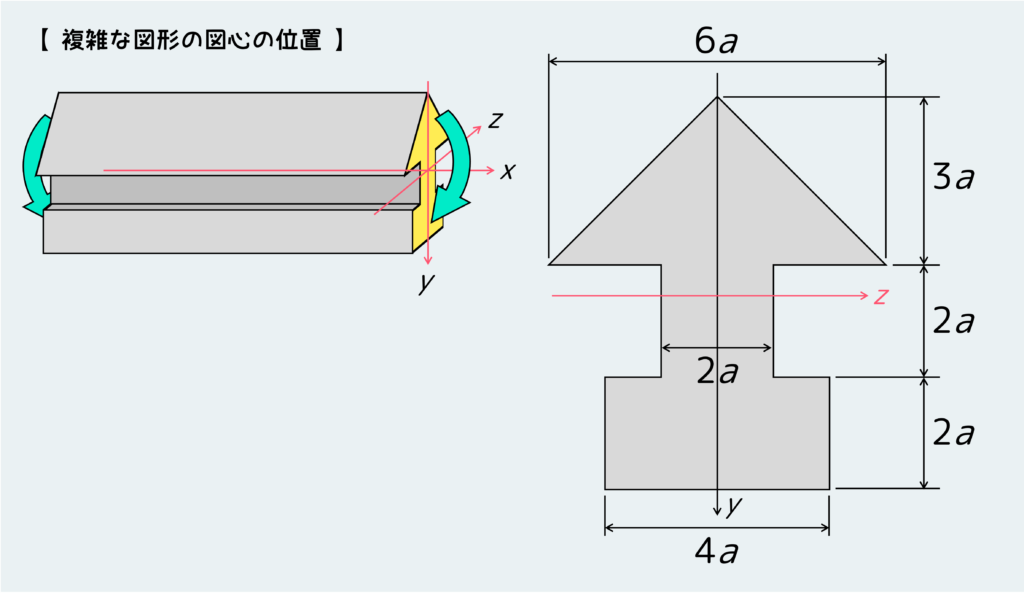
図心を見つけるってのはつまり、この断面形状の薄い板を想定してこれの重心を見つけることと同じだ。
なので、面積を重量のようにみなして回転モーメントがバランスするような点を見つければ、その点が重心(図心)になる。これは言葉で説明しても分かりにくいので、もう具体例を見てもらった方が早いと思う。
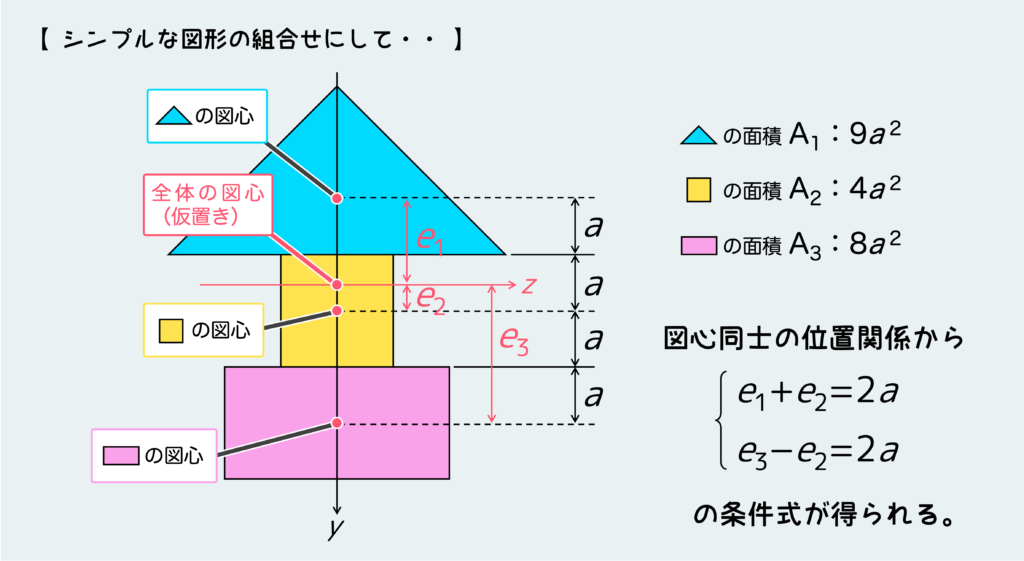
まず断面図形をシンプルな形のパーツに分解する。図心同士の位置関係から上のように条件式がいくつか得られる(分解したパーツの数による)。
そしてそれぞれのパーツの図心にそのパーツの面積が重量として働いているとして、ある仮置きした全体の図心を中心に回転モーメントを考え、その合計が“0”になるような条件を見つける。
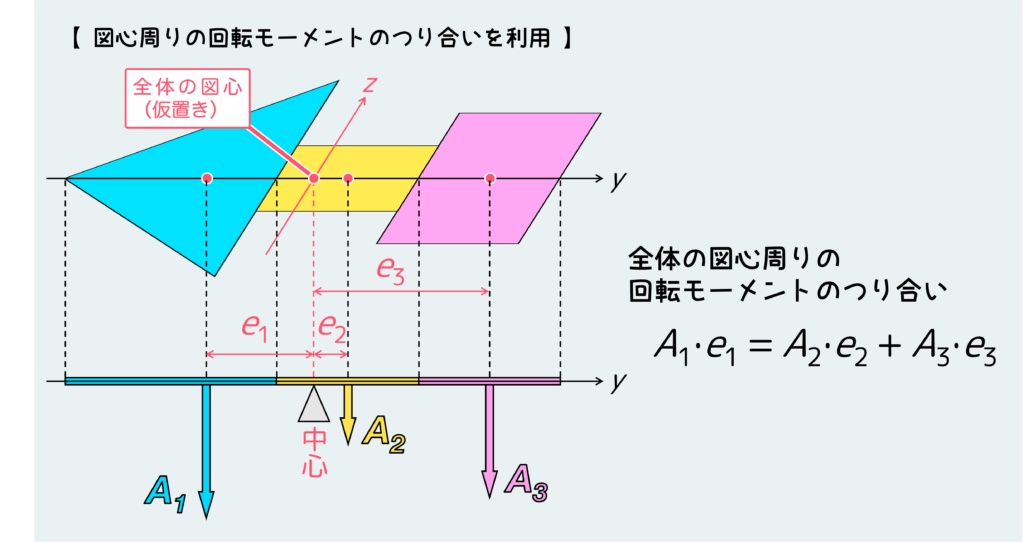
得られた条件式を整理して、図心の位置を決定できる。
使うべき断面二次モーメントを正しく見極める
断面二次モーメントについても注意が必要だ。下の図のように、断面二次モーメントは、同じ形状でも基準とする軸の位置によって変わってしまうのだ。
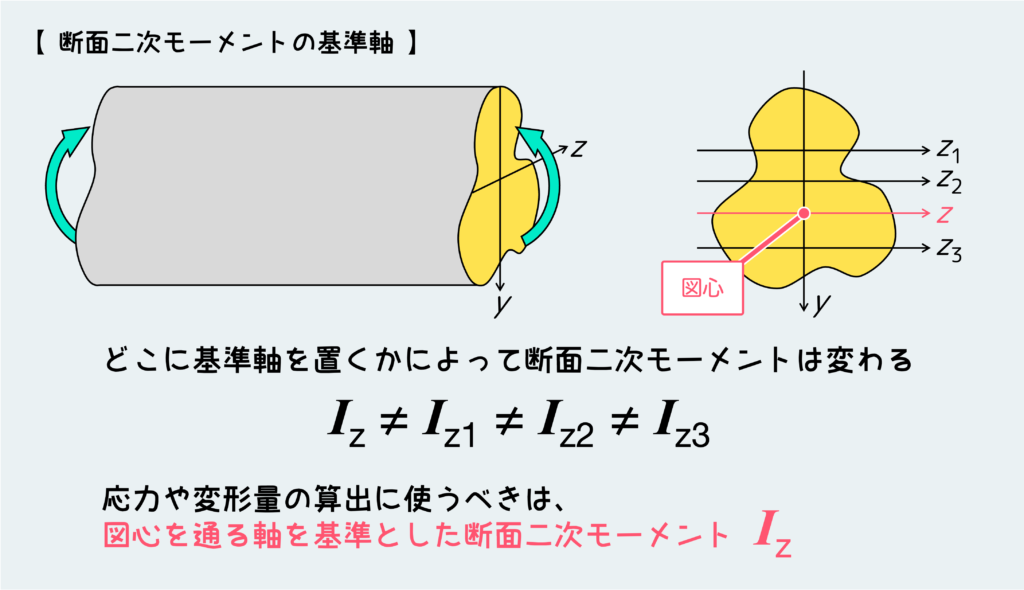
どの位置に基準軸を持ってくるべきか?と言うと、結論としては図心および中立面を通るように基準軸を設定しなくてはならない。このように、図心および中立面の位置を意識して、正しく導いた断面二次モーメントを用いて応力計算することが重要である。
とは言ってもほとんどの一般的な図形のときはあんまり気にする必要はない。なぜなら、多くの教科書で下のような断面二次モーメントの一覧が記載されており、ここに載っている断面二次モーメントはちゃんと図心を通る軸に関する断面二次モーメントになっているからだ。
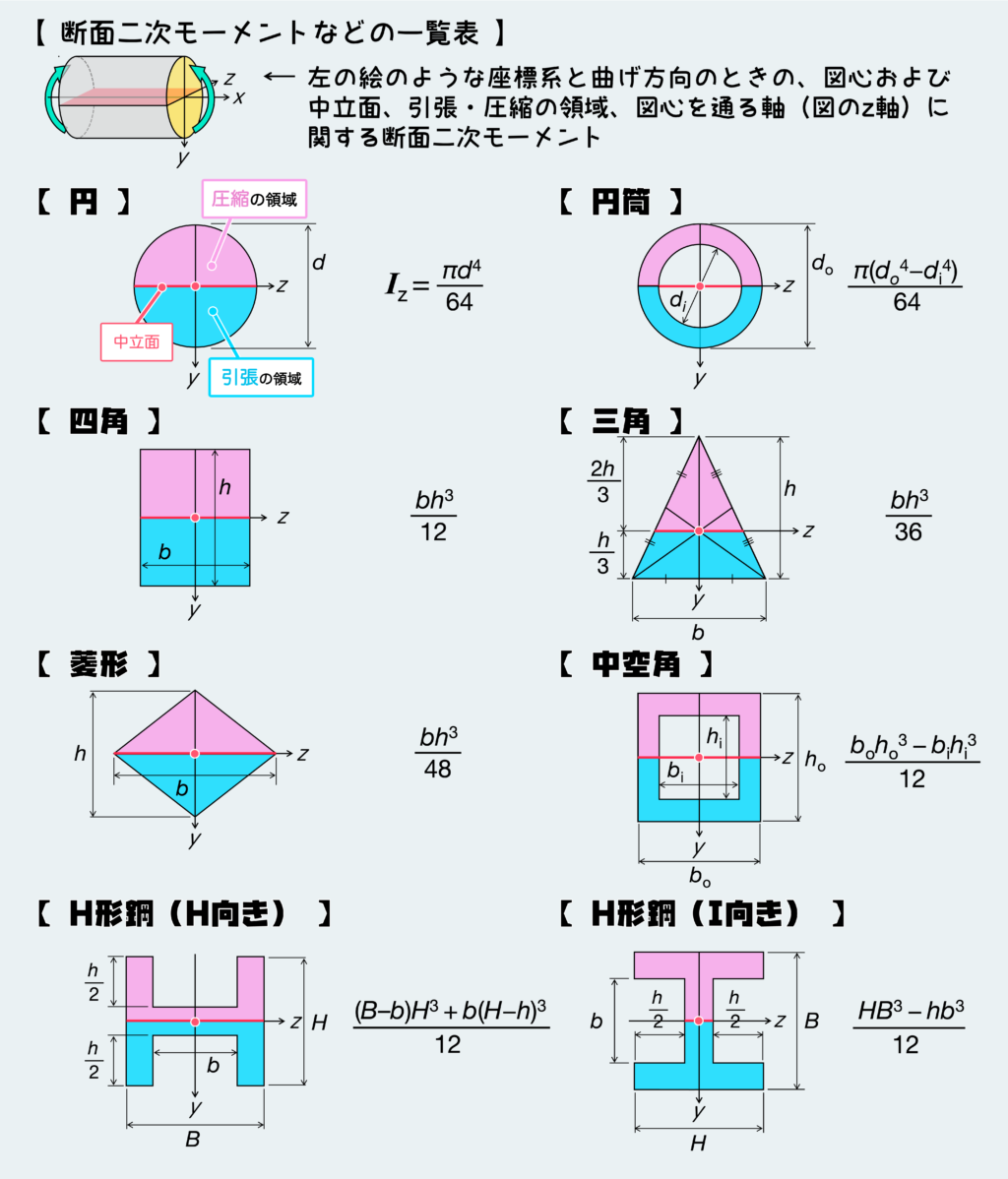
注意が必要なのはここに載っていないような断面形状のときだ。ここでは、複雑形状の断面二次モーメントの導出については省略する。これについて確認したい人は次の記事を見てほしい(現在執筆中)
BMDを利用して曲げ応力の全貌を完全把握せよ!
次に、手順STEP.3で書いた「曲げモーメント」について、だ。
前の記事でSFD・BMDというのを説明してきたが、曲げ問題の大きな特徴は『位置によってそこに伝わる内力である曲げモーメントが変化する』点だ。
冒頭にも言ったように応力を決定しているのは、そこに働く内力なので、曲げモーメントが変化すれば当然曲げ応力も変化することになる。なので、大事なことは今自分が応力を求めようとしている断面に働いている曲げモーメントを把握した上で、応力計算を行うことだ。
下図のように、先端に荷重を受ける片持ちばりを例に考えてみよう。例えばこのはりの中で最大の曲げ応力がどこに働くのか?またその大きさはいくらか?ということを知りたいとする。
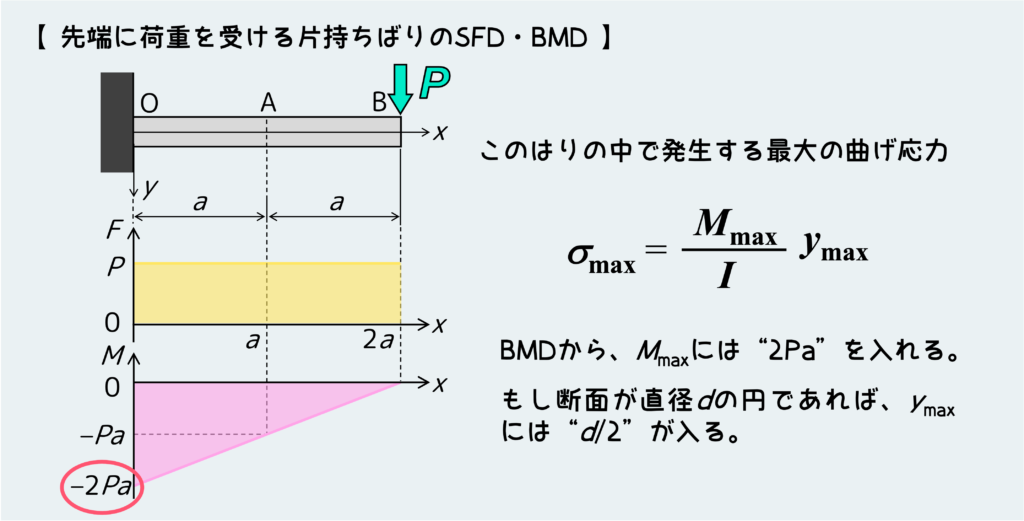
その場合はこのはりのBMDを描いて、最大の曲げモーメントが「どこに」「どんな大きさで」発生するかを理解しないといけない。断面形状が一様であれば、最大の曲げ応力が発生するのは最大の曲げモーメントが作用する箇所になる。
また、ある特定の箇所に働く応力を知りたいケースも考えられる。例えば、このはりはAの位置で溶接によって接合しており、母材に比べてこの溶接強度が低いため、この位置に発生する応力を知りたい、みたいなケースだ。
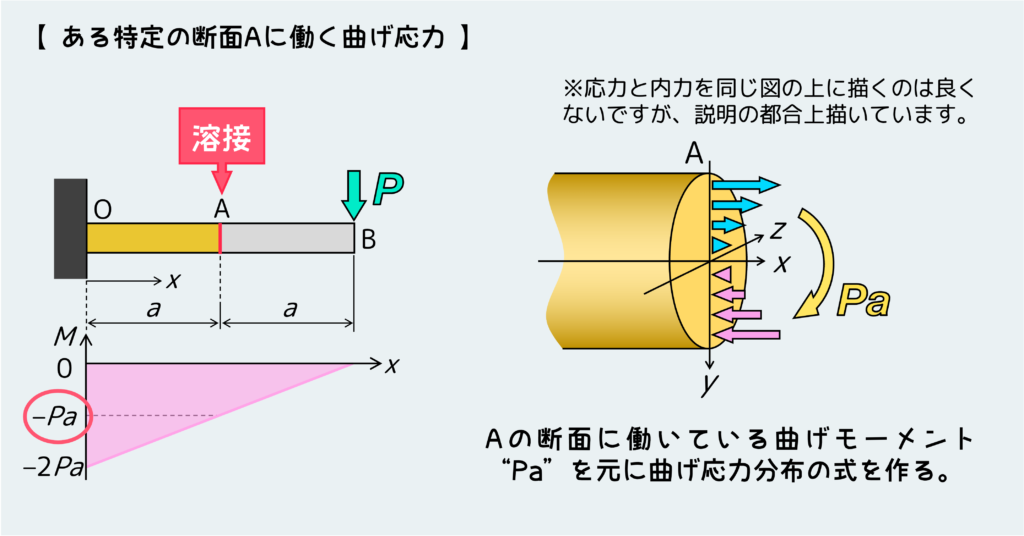
こんな時もBMDを利用して、応力が知りたい位置(断面)に働く曲げモーメントを見積もってやり、これを元に応力計算をする必要がある。
まとめ
かなり長くなってしまった。
でも曲げによる応力の考え方をかなり噛み砕いて説明したので、初学者の方にはタメになったものと信じている。
ここまで説明してきたように、曲げ応力を理解するためには『BMDを利用した曲げモーメントの考え方』と『断面二次モーメントの考え方』を習得していないといけないので、よく分からないという人はこれらのことを解説した別記事もぜひ読んでみてほしい。
 材料力学 SFD/BMDって何?その意義を超詳しく解説【材力Vol. 6-1】
材料力学 SFD/BMDって何?その意義を超詳しく解説【材力Vol. 6-1】
 材料力学 絶対描けるようになるSFD/BMDの描き方を徹底解説【材力Vol. 6-2】
材料力学 絶対描けるようになるSFD/BMDの描き方を徹底解説【材力Vol. 6-2】
 材料力学 すっきり理解できる断面二次モーメントの意味【材力Vol. 6-5】
材料力学 すっきり理解できる断面二次モーメントの意味【材力Vol. 6-5】
- 曲げを受ける材料の断面には、中立面を境にして引張応力と圧縮応力が同時に働く。中立面から離れるほど大きな応力が発生する。
- 曲げ応力を求めるには、曲げモーメントと断面二次モーメントおよび中立面(図心)の位置を正確に把握することがとても重要。