私ぽるこがまとめる材料力学シリーズもVol.3まできましたが、いよいよ引張・圧縮問題について説明していこう。ここまで材料力学の基本である自由体の考え方や応力・ひずみについて説明してきたが、より具体的、実践的な内容としてここから引張・圧縮、ねじり、曲げといった負荷形態について詳しく説明していきたいと思う。
まずこのVol.3では引張・圧縮についてとりあげたい。比較的簡単だとは思うが、いくつかのポイントがあるので、しっかりこれを押さえながら勉強してほしい。ここで基本的な考え方をマスターしておけば、のちのねじりや曲げの問題でも役に立つはずだ。
まずこの記事では、引張や圧縮といった負荷によって材料に起こる変形および発生する応力やひずみについて詳しく説明していきたい。
すでにある程度勉強している人も基本に立ち戻る意味でぜひ一読してほしい。
- 引張(もしくは圧縮)を受ける材料に発生する(引張軸方向の)応力は、作用している荷重を引張軸に対して垂直な断面積で割ることで計算できる。
- 引張・圧縮を受ける材料の(引張軸方向の)ひずみは、その方向の材料の元の長さに対する材料の伸びの比率で表せる。つまり、伸びを元の長さで割ることで求まる。
- 引張・圧縮を受ける材料(ここでは棒材とする)の変形量(伸び、縮み)\(\lambda\)は、荷重Pと棒の長さlに比例し、断面積Aに反比例する。このとき比例係数を1/Eで表し、このEがヤング率(縦弾性係数)と呼ばれるものである。引張・圧縮による変形量を表す式は以下の通り。
- \(\lambda=\displaystyle \frac{1}{E} \cdot \frac{Pl}{A}\)
Contents
引張・圧縮による応力
ここでは最もシンプルな両端に引張荷重を受ける棒を考えよう。複雑な問題も結局はこの形に分解(自由体の考え方)してから考えることになるので、このシンプルな形で考え方もマスターしておけば何も怖くない。
ここでは断面形状はどうでもいいので、下図のように丸棒の両端に荷重がかかる場合を考える。
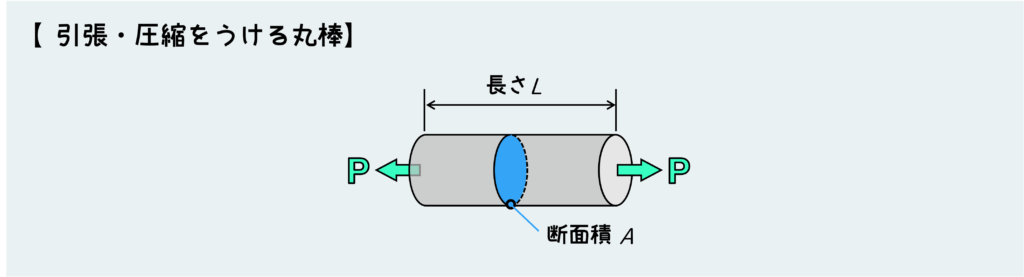
前の記事(材料力学 応力とは?10分で完全に理解できる 基本かつ超重要な解説【材力 Vol. 2-1】)でも説明したが、応力を考えるためにはある断面に働く内力を知る必要がある。その面に働く内力が応力状態を定義することになる。
では、両端に引張を受ける棒の内力の伝わり方はどうなっているだろうか?内力を知るためには、自分の知りたい位置で仮想的に材料を切断し、平衡条件をもとに力の伝わり方を決定する(自由体の考え方)。
下図のように、この棒の適当な位置で切断して、この断面に働く内力を考える。すると、この棒の横断面(こういう棒材の場合、長手方向を縦、それに垂直な方向を横と言うことが多い)に対しては、どの位置で見ても同じ引張力Pが働いていることが分かる。
つまり、この引張の内力Pによる応力は何か?ということになる。
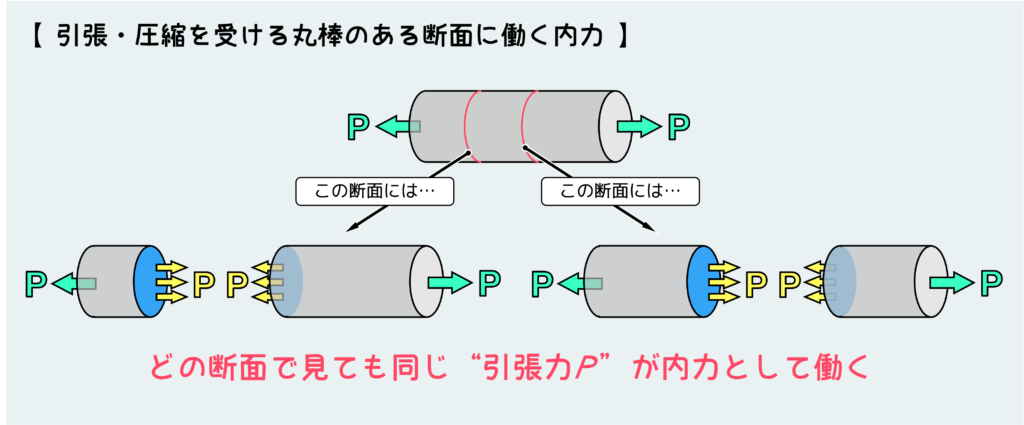
一般的に材料力学においては、この引張の内力Pは断面上に一様に働いているとみなして考える。(一様とならない場合は後述する)
この場合、この引張力Pによる応力σは、単純に引張力Pを断面積で割った大きさとなるので\(\sigma=\displaystyle\frac{P}{A}\)と表せる。ちなみにこの引張応力は、面に垂直な方向に作用するので垂直応力だ。
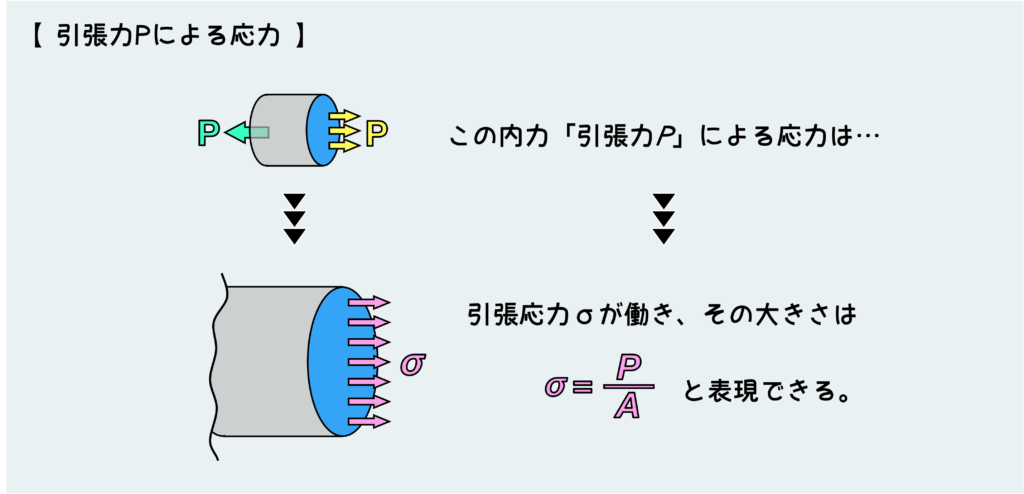
この引張圧縮問題で、断面形状(丸なのか四角なのか?みたいな)は関係ない。断面積だけで応力は決まってしまう。
もし棒が直径dの丸棒であるならば、これが引張荷重Pを受ける場合、この棒のある横断面に働く垂直応力σは、\(\sigma=\displaystyle\frac{4P}{\pi d^2}\)と表せる訳だ。
引張圧縮の多くの場合、問題とされる応力は上記のように表現できるが、そう単純じゃないパターンもある。
盲目的に“引張問題=応力は荷重を断面積で割ればいい”のように考えるのではなく、なぜそうなのかをよく理解してほしい。次の注意点をよく読めば、このことがよく理解できると思うのでぜひこの後も読んでほしい。
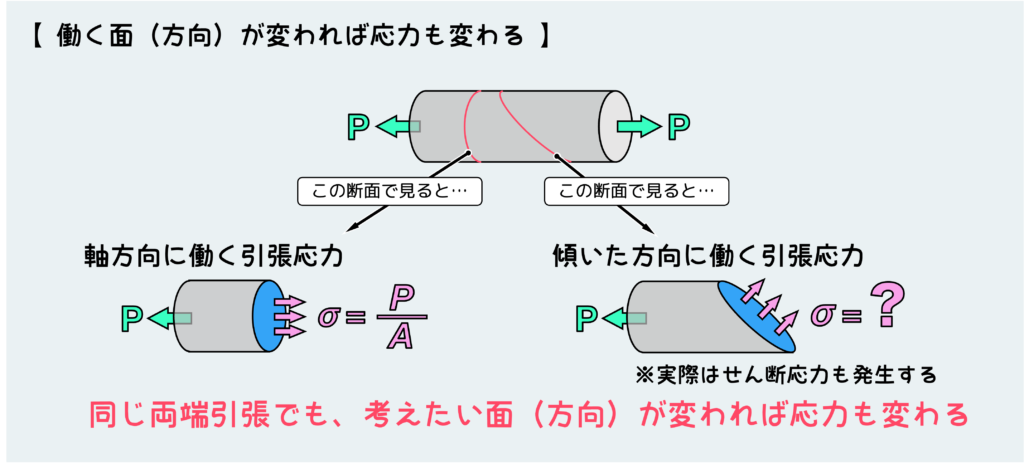
引張圧縮問題で最も一般的に問題とされる応力は、横断面に働く垂直応力であり、ここまではこれに焦点を当てて説明してきた。
しかし、そうじゃないパターンも存在する。例えば下図の右側のように、傾いた面に働く応力が知りたい場合だ。
この図のように、引張方向から傾いた面に働く垂直応力は\(\sigma=\displaystyle\frac{P}{A}\)とはならない。
じゃあどんなシチュエーションのときに、こんな傾いた面の応力が知りたくなるだろうか。考え得るものとしては溶接問題がある。
元々の棒が、上図のように傾いた面を溶接してくっつけて作製したものだとしよう。さらに、この溶接部の強度(どれぐらいの応力に耐えられるか)は母材(溶接でくっつけた元の材料)の強度よりも低いとしよう。実際こんな状況は山ほどある。
こういうときは、前のパートで説明してきた横断面に働く垂直応力ではなく、この傾いた面に働く応力がどれくらいか?ということの方が重要になる(この傾いた面に働く応力が溶接強度を超えると溶接部から破壊する)。
このように、状況によっては単純に引張荷重Pを断面積で割っただけの応力(横断面に働く応力)ではなく、別の応力を考える必要があるので、最も単純な\(\sigma=\displaystyle\frac{P}{A}\)が意味している応力の意味をよく理解しよう。
ちなみに、この傾いた面の応力はどうやって考えるのか?については応力変換というテクニックが必要になる。これについては別の記事で説明する予定だ。
上で説明してきた“引張応力=荷重を断面積で割る”は多くの場合において正しい考え方だ。ただし、これには前提があり、応力が断面上に一様に分布しているものとみなしているという点に理解が必要だ。
一様に分布する応力というのは、下図のように断面上のどの点をみても同じ大きさの応力が働いているということだ。だが実際にはこうならないケースもある。

それは例えば下図のような場合だ。
両端引張と言ってもいろんなやり方がある。下図の左側は端面の中央1点を持って引っ張るやり方で、右側は端面の両端を持って引っ張るやり方だ。かかってる荷重はどちらもPで同じなので、上で説明してきた“引張応力=荷重を断面積で割る”の考え方に基けば、両者とも同じ応力が作用していることになる。
しかし実際はどうかというと、特に端面(荷重が作用している面)にすごく近い位置の横断面の応力を考えた場合、荷重がかかっている点の位置に依存して応力に一様ではない分布ができてしまう。
左の場合は、中央を持って引っ張っているので、その近くの断面でも中央部分に大きな応力が発生する。
右の場合は、端の方に大きな応力が作用し、中央付近は逆に小さくなるような応力分布が生じる。
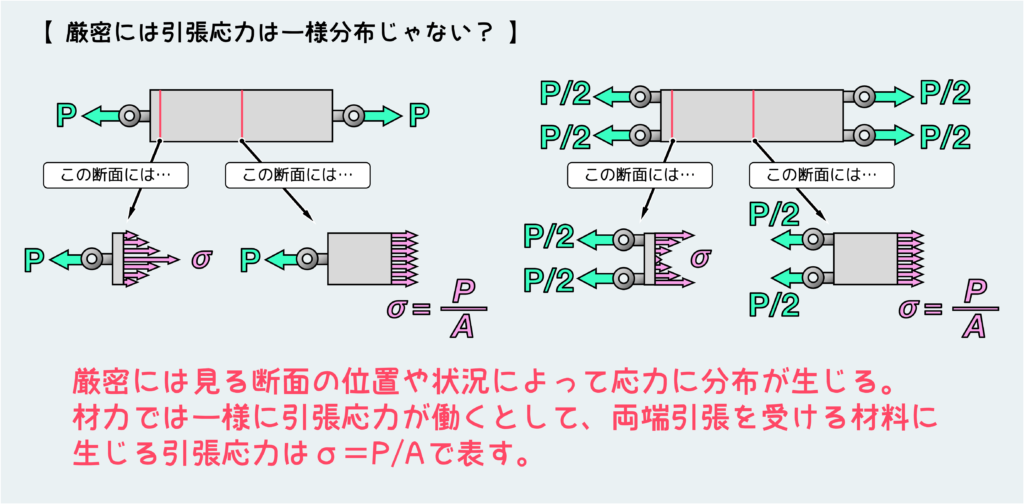
このように外力が働いている位置の直近では応力分布は一様ではなくなる場合があるので、このような断面においては\(\sigma=\displaystyle\frac{P}{A}\)は成り立たない。
しかし両ケースともに、端面から十分離れた位置では応力分布は一様になる。このような外力が作用している位置から十分離れた横断面に働く応力はやはり\(\sigma=\displaystyle\frac{P}{A}\)で表せることになる。
なので材料力学においては、外力が働いている位置の直近のような極端な位置ではなく、十分離れて応力分布が落ち着いた位置における応力やひずみのことを述べている、と思えばいい。ただし、上の例のように、そう単純に考えてはいけない状況があることも頭に入れておいてほしい。
引張・圧縮による変形
では次に変形について説明したい。例によって、すごくシンプルな例として両端に引張荷重を受ける材料を考える。今度は板状の材料について考えてみよう。
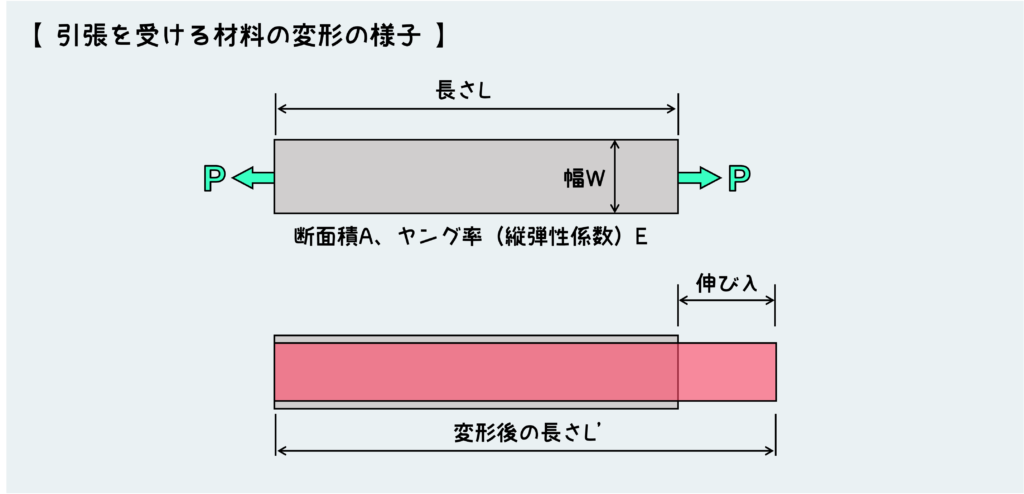
この板材を両側から引っ張ると、上の赤く塗った部分のようになることが想像できると思う。
この変形量のことを伸び(圧縮の場合は縮み)と言うが、この伸びはどんな特徴を持ってるだろうか。リアルに変形をイメージすることで、伸びの持つ特徴を考えてみよう。
ここで考えたいことは、『何がどう変わると伸びは増えたり減ったりするか?』ということだ。こういうことは日常生活で体験していることのはずで、こういうイメージができるかどうかは材料力学においてとっても重要なことだ。
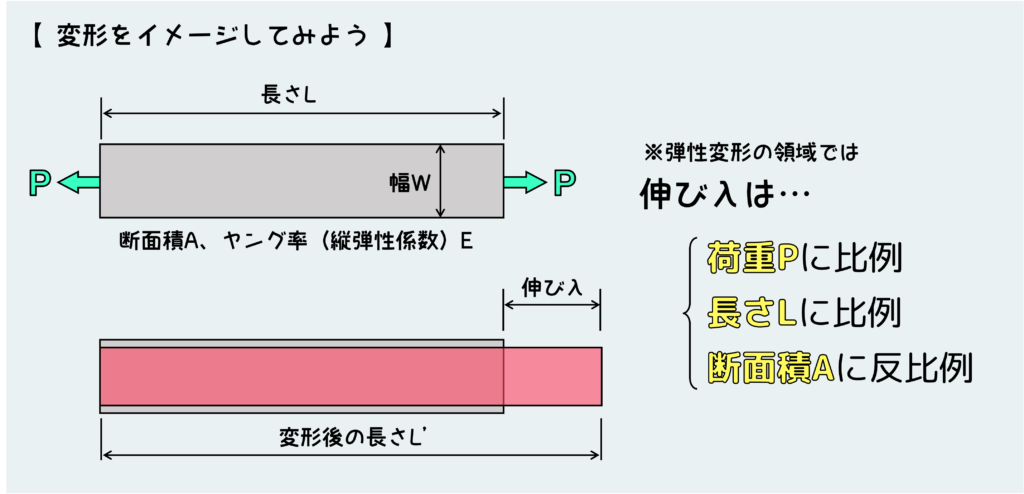
さて、正解はと言うと下図のようになる。
荷重Pが大きいほど、また長さLが大きいほど、この材料の伸びは大きくなる。さらに断面積Aに関しては小さいほど伸びは大きくなる。このことが感覚的にイメージできるだろうか。
ただし、絶対に忘れてはいけない前提条件がある。今説明したこと(下図)は、材料が弾性変形しているときの話だ。材料力学で取り扱う材料は基本的に金属材料だと思うが、金属のような材料には、弾性変形と塑性変形の2種類の変形がある。
比較的小さな変形をするのが弾性変形で、これ以上に大きな変形を与えると材料は塑性変形という挙動を示すようになる。この辺のことはまた別の記事で機会があれば説明したいと思うが、とにかく下図のような関係性は材料が弾性変形しているときの話だ。材力では基本的に弾性変形を取り扱うので、この関係性を理解しておくのは非常に重要だが、弾性変形と塑性変形では全く違う挙動を示すことを忘れないでほしい。
 材料力学 フックの法則が使える時と使えない時の違いちゃんと分かってる?【Vol. 2-3】
材料力学 フックの法則が使える時と使えない時の違いちゃんと分かってる?【Vol. 2-3】
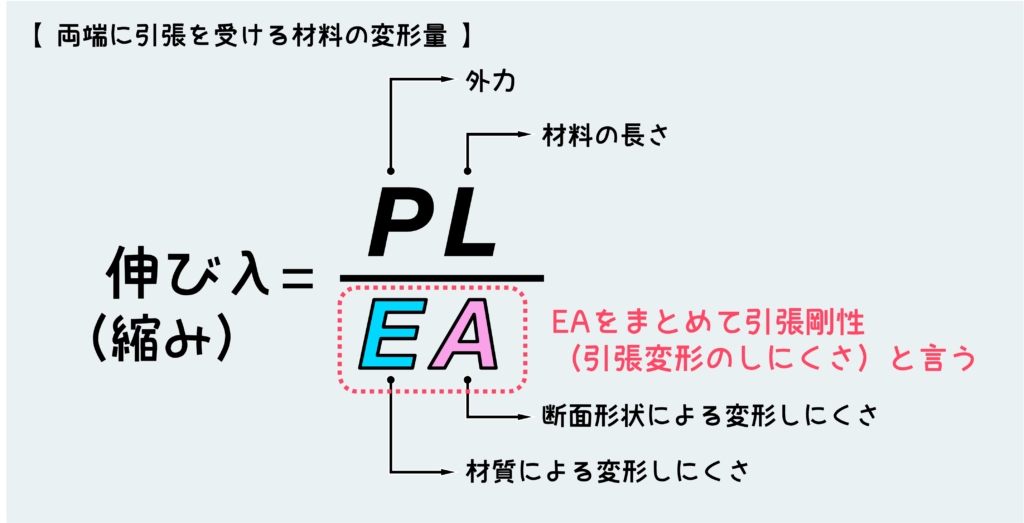
ではもっと踏み込んで、この変形量を数式化してみよう。荷重Pと長さLに比例して、断面積Aに反比例するので、下図のような式で伸びを表すことができる。ここで1/Eが比例定数という訳だ。
このEはヤング率とか縦弾性係数と呼ばれるもので、材料の形状や寸法には関係なく、材質によってのみ決まる材料物性値である。Eが大きいと変形しにくくなり伸びは小さくなる、Eが小さいと小さな荷重でも大きな変形を示すことになる。
Eのことを広い意味で「剛性」と表現する場合もあるけど、基本的には断面形状も含めて“EA”を「引張剛性」と言ったり単に「剛性」と言うことの方が多いかと思う。剛性と言うのは変形の起こりにくさという意味だ。
引張を受ける材料の変形(伸び)は、下図のように『(外力)×(材料の長さ)を(材質による変形しにくさ、ここではE)×(断面形状による変形しにくさ、ここではA)で割る』という形で表現できるが、これは他の負荷形態である「曲げ」や「ねじり」の場合も似たような表現になるので、この形はしっかりと覚えておくことをオススメする。
次にひずみについて説明していきたい。
まずひずみの定義についておさらいしておくが、「ひずみ」というのは“変形の割合”を表すので、元のサイズに対する変形量の比で表せる。
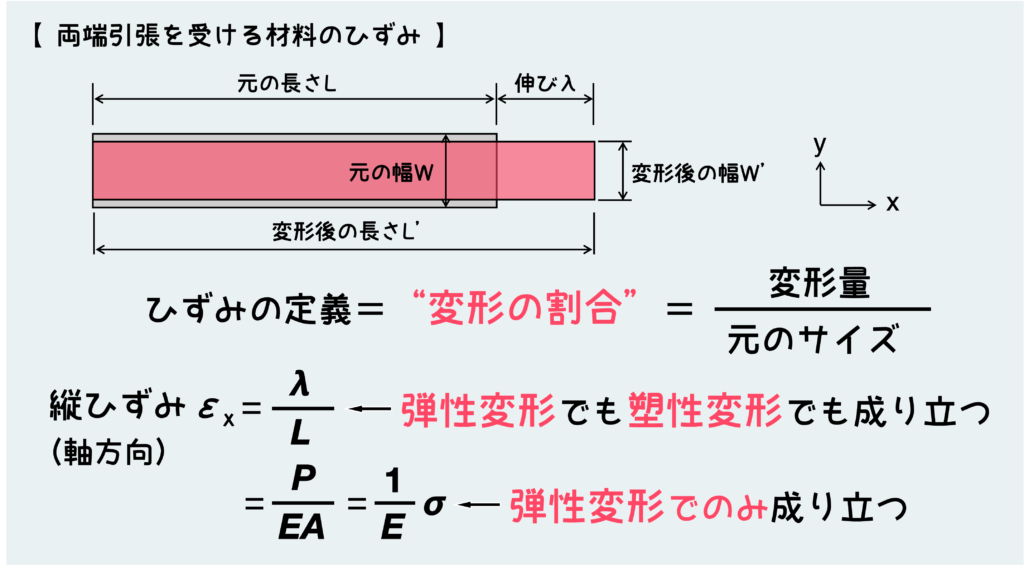
なので、縦ひずみ(上図でx方向、つまり引張方向のひずみ)は、伸びλを用いて、λ/Lで表現できる。これはひずみの定義に基づくものなので、変形が弾性変形だろうが塑性変形だろうが成り立つ。
例えば、長さ100mmの鉄鋼材料を引っ張った結果、20mm伸びたのであれば(伸び)20mmを(元の長さ)100mmで割って0.2、つまりひずみは20%だ。一方0.1mmしか伸びなかったのであれば、同様な計算からひずみは0.1%だと言える。前者が塑性変形で、後者は弾性変形だが両者ともに同じ計算式でひずみを求めることができる。
一方で、よくひずみεを\(\displaystyle\frac{1}{E}\cdot\sigma\)と表現される(フックの法則)が、これは弾性変形でしか成り立たない。
この辺のことは下の記事に詳しく書いているので、ぜひ読んでみてほしい。
 材料力学 フックの法則が使える時と使えない時の違いちゃんと分かってる?【Vol. 2-3】
材料力学 フックの法則が使える時と使えない時の違いちゃんと分かってる?【Vol. 2-3】
リアルに変形を想像すると分かると思うが、引っ張った方向に対して垂直な方向には逆に縮もうとする。
なので下図のようにx方向に引っ張って伸びた場合、y方向には縮む。さらに、引っ張った方向のひずみ(εx)とその垂直方向のひずみ(εy)の大きさには材質に依存した一定の比率があり、これをポアソン比(ν、ブイじゃなくてギリシャ文字のニュー)と呼ぶ。
一般的な鉄鋼材料の場合、ポアソン比は約0.3だ。その他の多くの金属材料でも0.3に近い値を取る。つまり、図のように引っ張った場合、x方向の伸びに対して30%ほどy方向には縮むことを意味している。
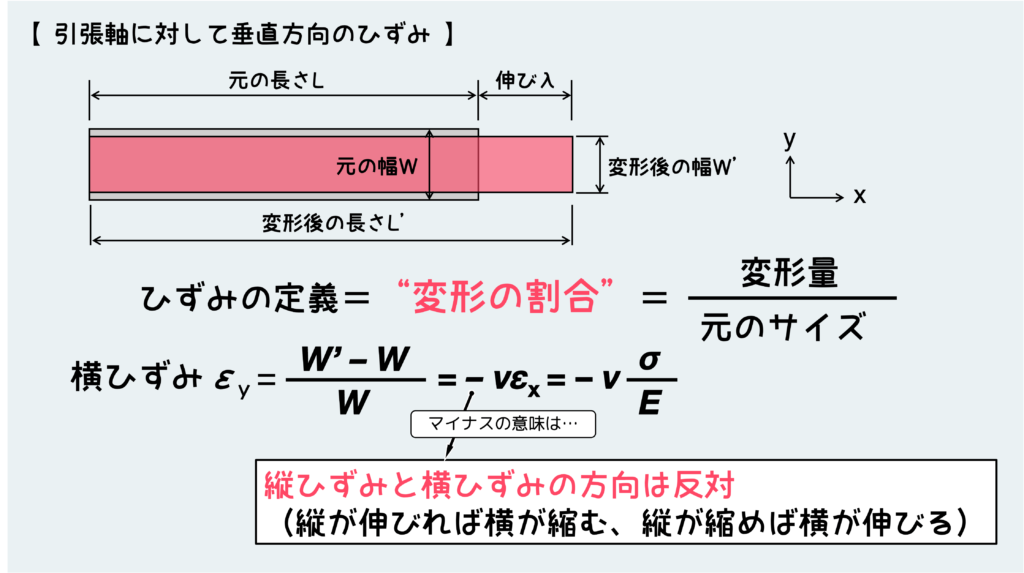
したがって、y方向のひずみεyは\(\epsilon_y=-\nu\epsilon_x\)と表せる。ここで付いているマイナスの意味は、引っ張ったことによるx方向のひずみとy方向のひずみが逆方向になることを意味している。
ひずみは伸びをプラスで、縮みをマイナスで表す。これはもう、そういう約束事だ。つまり、x方向に伸びたのならy方向には縮むし、もしx方向に圧縮荷重をかけて縮んだのなら、y方向には伸びるという訳だ。
今回は一軸(荷重が一方向に作用している)の問題を扱ったが、これが二軸になるとポアソン比の関わり方が少しだけ複雑になる。二軸あるいは三軸のフックの法則と呼んだりするが、これについてはまた別の記事で取り扱おうと思う。
まとめ
今回は、説明しやすさだったり理解のしやすさを考慮して、変形を考えてからそれを元にひずみを説明した。しかし、実際には応力を元にひずみが定義でき、これに基づき変形量(今回は伸び)が決まるのが物理的に正しい流れだ。
まあ人によっては難しく感じるかもしれないので、ひずみを元に変形量を計算するのは今回は省略させてもらった。また機会があれば説明したいと思う。
とにかく今回の記事では、単純な引張をうける材料の応力・変形・ひずみの要点を押さえてほしい。材力の基本中の基本だ。
次の記事からはもう少し具体的な引張・圧縮の問題の解き方について説明していきたい。
- 引張(もしくは圧縮)を受ける材料に発生する(引張軸方向の)応力は、作用している荷重を引張軸に対して垂直な断面積で割ることで計算できる。
- 引張・圧縮を受ける材料の(引張軸方向の)ひずみは、その方向の材料の元の長さに対する材料の伸びの比率で表せる。つまり、伸びを元の長さで割ることで求まる。
- 引張・圧縮を受ける材料(ここでは棒材とする)の変形量(伸び、縮み)\(\lambda\)は、荷重Pと棒の長さlに比例し、断面積Aに反比例する。このとき比例係数を1/Eで表し、このEがヤング率(縦弾性係数)と呼ばれるものである。引張・圧縮による変形量を表す式は以下の通り。
- \(\lambda=\displaystyle \frac{1}{E} \cdot \frac{Pl}{A}\)




