材料力学　SFD・BMDの押さえておきたい大事な特徴と４つの特定パターン【材力Vol. 6-3】

このブログでは「プロモーション」が含まれています。

前の記事でSFD・BMDの意義そして具体的な描き方を解説してきた。

今回の記事では、SFD・BMDの大事な特徴と、材料に加えられる負荷の種類に応じてSFD・BMD上に現れる４つのパターンについて説明したい。

この記事に書いてあることを知ればSFD・BMDのことをより深く理解できる。計算をしなくてもある程度グラフの形を描けるようになったりもする。計算間違いに気付くきっかけになることもある。とっても便利なので、ぜひ最後まで読んでほしい。

SFD・BMDの意義についておさらいしたい人は、これを読んでから戻ってきてほしい。

材料力学　SFD/BMDって何？その意義を超詳しく解説【材力Vol. 6-1】

具体的な描き方について知りたい人は、この記事を読んでからまた来てほしい。

材料力学　絶対描けるようになるSFD/BMDの描き方を徹底解説【材力Vol. 6-2】

いろんな問題の解き方のパターンを見たい人は下の記事をどうぞ。

材料力学　６つの具体例から学ぶSFD・BMDの重要ポイント【材力Vol. 6-4】

この記事でわかること

超基本的な性質：「BMDの傾きが同じ位置のSFDのFの値になる」
何も負荷を受けていないところ：SFDは一定値（水平）、BMDは傾きFの直線
集中荷重Pが働く点の前後：SFDは大きさPの段、BMDは傾きがPだけ急変するような角
モーメントM₀が働く点の前後：SFDは一定値（水平）、BMDは大きさM₀の段
分布荷重（密度q）が働く領域：SFDは傾き”-q”の直線、BMDは二次関数

夢へ駆ける少女の姿に感涙！！

メダリスト / つるまいかだ

12巻連載中

「司先生は…っ　　わたしが世界一になりたいって言ったら手伝ってくれますか？」

2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。

「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい！」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。

ebookjapanなら2/4までなんと3巻無料で読めてしまいます！まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです！

Amazonで探す

楽天で探す

ebookjapanで読む

私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！

この記事を読む

Contents

超基本的な性質
材料が受ける負荷の状況とSFD・BMDに現れるパターン
まとめ

超基本的な性質

まず、特定パターンの説明をする前に、SFD・BMDの超基本的な性質について紹介しよう。

絶対に分かっておくべきSFD・BMDの基本的な性質は以下の通り。

これはどういうことかと言うと、ある位置においてBMDのグラフの傾きが同じ位置のSFDのFの値になる、ということだ。

これを理論的に証明することもできなくはないが、あまり興味がある人も多くないだろうから省略する。とにかく『BMDの傾き＝SFDの値』ということを覚えておこう。

では、具体的なパターンを見ながらこの性質がどんな風に現れるか確認していこう。

材料が受ける負荷の状況とSFD・BMDに現れるパターン

では、超基本的な性質が分かったところで、はりが受ける負荷の種類に応じてSFD・BMD上にどんな変化が現れるか具体的なパターンを見ていこう。

これを全部理解できれば、計算せずともおおよそのグラフの形が分かるようになるだろう。また、自分の解答が正しいかどうかを簡単にチェックするときにも便利なので、ぜひ理解してほしい。

何も負荷を受けてないところ

まずは何の負荷も受けていない所で、SFD・BMDがどんな形になるか見てみよう。ほとんどの問題ではりの大部分はこれ（何も負荷がかかっていないところ）なので、SFD・BMDの大部分も下の絵に描いたような形になる。

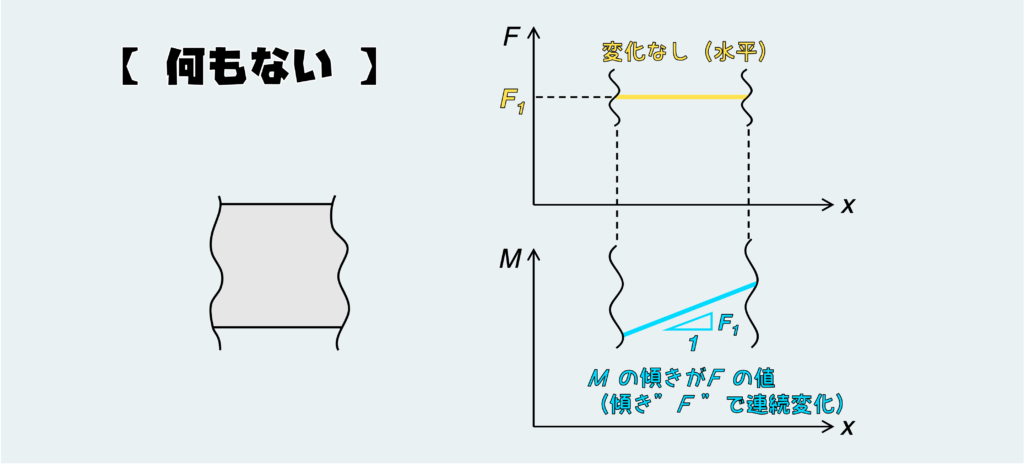
SFDについては変化なしで、グラフ上では ”水平” になる。値自体（上の図ではF₁）はどうなるか分からない。このはりのどこかに作用している外力や支持条件によって決まる。だけどとにかく形は水平だ。何かしらの値で一定値となる訳だ。

BMDについては基本の性質を思い出そう。”BMDのグラフの傾きが同じ位置のFの値になる”が絶対ゆずれない性質だ。てことは、SFDがある値（上図ではF₁）で一定ということは、BMDは傾きF₁の直線（一次関数）となる。

何も負荷を受けていない所では・・

SFDは何かしらの値で一定値（水平）となり、BMDは傾きFの直線となる。

集中荷重が働くところ

では次に集中荷重が働くときを考えよう。

集中荷重が図のように上から下向きに作用するところでは、その前後のSFD・BMDは下のようになる。

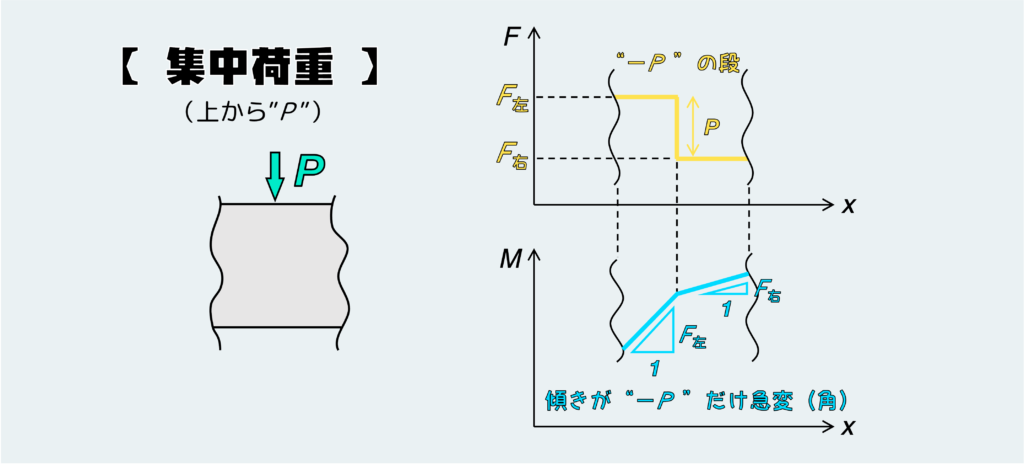
まず、SFDは集中荷重が働くその点でガクッと ”段” が付く。その段の大きさは、そこに加わってる外力の大きさと同じだ。上図のSFD内のF_左やF_右は、その他の外力や支点の状況によって決まる。

BMDについては、やはりBMDとSFDの関係性から上図のようになる。つまり、集中荷重が働く点の前後でSFDのFの値が急変する（Pだけ段が付く）ということは、BMDのグラフの傾きが急変することを意味する。集中荷重が作用する点の左側では傾き：F_左、右側では傾き：F_右となるので、BMDグラフ上では ”角” となって現れる。

集中荷重Pが働く点の前後では・・

SFDは大きさPの段となり、BMDでは傾きがPだけ急変するような角となる。

モーメントが働くところ

次は外力としてモーメントが働くときの場合だ。

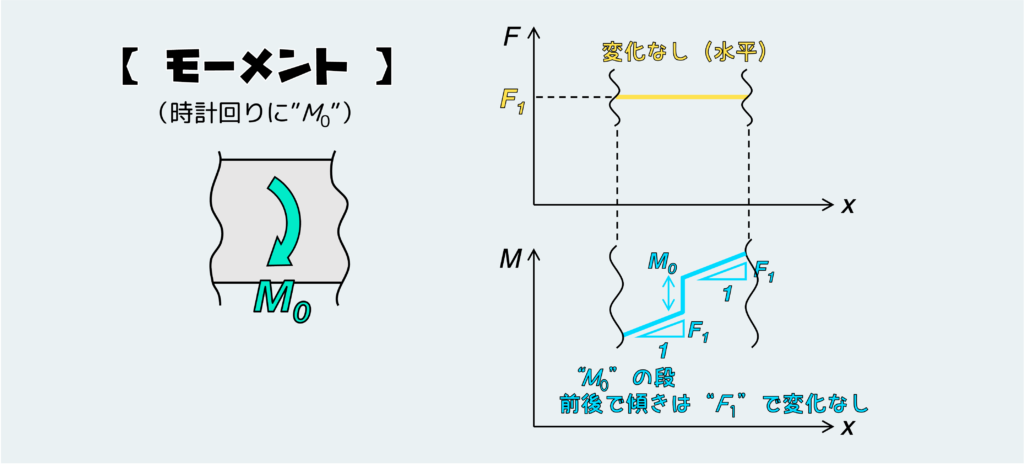
SFDは変化なしだ。何も負荷を受けていないときと同じで、ある値で ”水平”（一定値）となる。

この一定値（上図ではF₁）は、やはり外力や支持条件によって決まる。

ではBMDはどうか？SFDが何も負荷を受けていないときと同じ形（一定値）となるので、BMDも同様に傾き一定のグラフとなる。何も負荷を受けていない場合と違うのは、集中モーメントが働いている分だけその点でガクッと ”段” が付くことだ。さきほどの集中荷重の場合では、SFDの方に荷重の大きさの分だけ ”段” が付いたが、今回はBMDの方にモーメントの大きさの分だけ ”段” が付くことになる。その前後でのBMDの傾きは変化しない（上図ではF₁で一定）。

モーメントM₀が働く点の前後では・・

SFDは一定値（水平）となり、BMDは大きさM₀の段となる。BMDの段の前後で傾きの変化なし。

分布荷重が働くところ

最後に密度qの分布荷重が作用する場合を考えよう。完成するSFD・BMDの形としては、これが一番複雑となる。

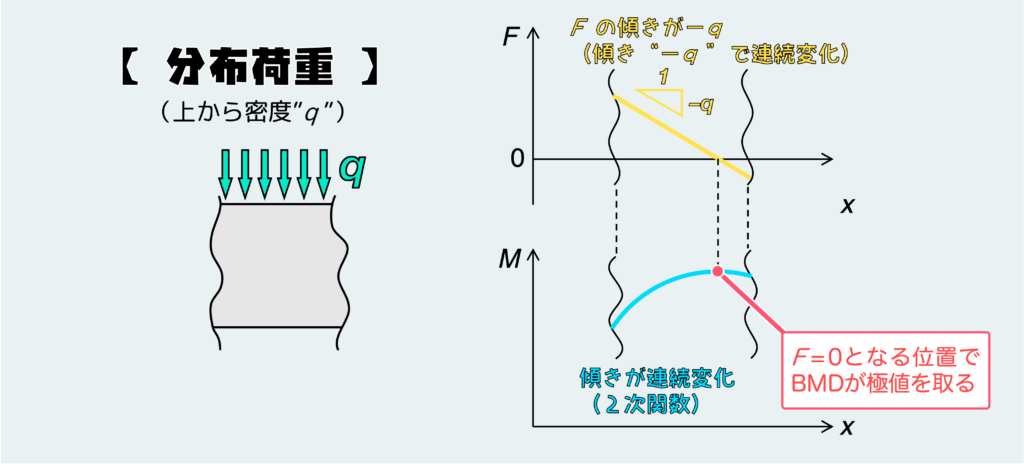
SFDでは、分布荷重が働いている領域全域で傾き”-q”の直線になる（他の外力がないとき）。今回も他の場合と同様に、この直線の縦軸方向の位置はその他の外力や支持条件によって決まる。

BMDの方は、SFDが連続的に変化していくのでこれを反映して、二次関数となる。二次関数を描くときの注意点は、ちゃんとSFDのFの値とBMDの傾きが連動するように描かないといけないことだ。

例えば、SFDのグラフでFの値が正（＋）の領域では、BMDは傾きが正であり、Mの値は増えていかないといけない。さらに、SFDのFの値が0に近づいてくるときはBMDの傾きもだんだん0に近づかないといけないし、SFDが0になる点ではBMDは傾きが0、つまり極値をとるように描かないといけない。上図をよく見て、SFDとBMDの対応関係がどういう風に現れているかよく確認しておいてほしい。

分布荷重（密度q）が働く領域では・・

SFDは傾き”-q”の直線となる。BMDは二次関数の形となり、極値を取る位置などSFDとの対応に注意。