前回の記事でSFDとBMDの意義について解説した。
今回は具体的なSFD・BMDの描き方について説明しよう。決められたステップを踏めば、誰でも間違いなくSFD・BMDを描けるようになると思う。ぜひマスターしてほしい。
SFDとBMDの意義についておさらいしたい人は、下の記事を読んでからこの記事に戻ってきてほしい。
 材料力学 SFD/BMDって何?その意義を超詳しく解説【材力Vol. 6-1】
材料力学 SFD/BMDって何?その意義を超詳しく解説【材力Vol. 6-1】
また、SFD・BMDを描く上で、絶対に理解しておいた方がいい性質について説明している下の記事もぜひ合わせて読んでほしい。
 材料力学 SFD・BMDの押さえておきたい大事な特徴と4つの特定パターン【材力Vol. 6-3】
材料力学 SFD・BMDの押さえておきたい大事な特徴と4つの特定パターン【材力Vol. 6-3】
いろんな問題の解き方のパターンを見たい人は下の記事をどうぞ。
 材料力学 6つの具体例から学ぶSFD・BMDの重要ポイント【材力Vol. 6-4】
材料力学 6つの具体例から学ぶSFD・BMDの重要ポイント【材力Vol. 6-4】
- SFD・BMDを描く手順は下のとおり。
- 片持ちばり以外の問題では、壁や支点から受ける反力を求めておく。
- 場合分けが必要か考える。
- 適当な所で切って(左端からこの位置までの距離を “x” とする)、自由体図を描く。
- 平衡条件から、切断面に働く内力(せん断力Fと曲げモーメントM)を求める。
- 求めたFとM(xの関数)をグラフ上に描く。
Contents
簡単な例題で描き方をマスターしよう!
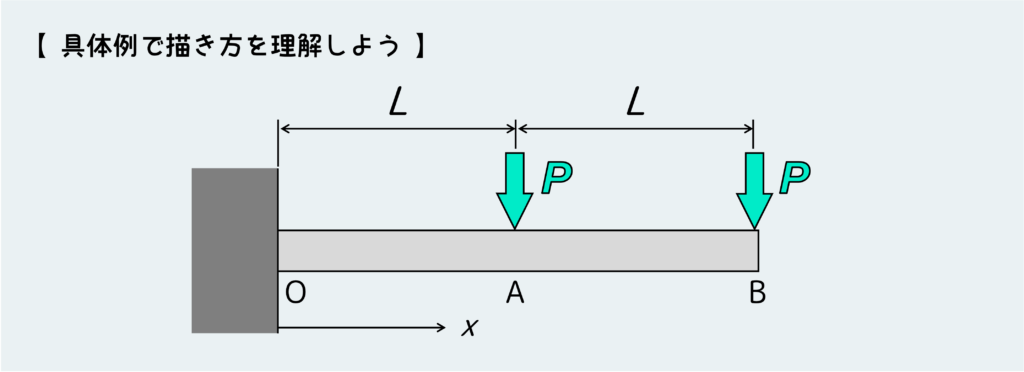
では、上図のような極々シンプルな例題をもとに、SFD・BMDの描き方を徹底解説していこう。
ズバリ手順に従えば、誰でも描けるようになるはずだ。
ズバリこの手順に従って描けば誰でも描ける!
基本的に次の手順を踏む事で、誰でも間違えずにSFD・BMDを描けるようになると思う。
はり全体を支点等から切り離して、自由体として取り出し、平衡条件から反力を求める。片持ちばりの場合はこのステップはスキップして良い。
はりを左から眺めていき、何か状況が変化するポイントでは場合分けが必要。
切断した断面には、正の向きにせん断力と曲げモーメントを仮置きする。はりの左端から切断した所までの距離をxとおく。
切断した位置をxとして平衡条件を考える。FとMは切断した位置xの関数として求まる。STEP.2で場合分けしたときは、場合分けの数だけ、STEP.3とSTEP.4を繰り返す。
横軸x、縦軸Fもしくは縦軸Mのグラフを描く。節目のポイントでは、xに具体的な数値(もしくは文字)を代入して、その位置でのFおよびMを求め、グラフに描き込むと良い。
片持ちばり以外のときはこのステップを最初に実行しよう。片持ちばりのときは飛ばしてよい。
理由を簡単に説明しよう。
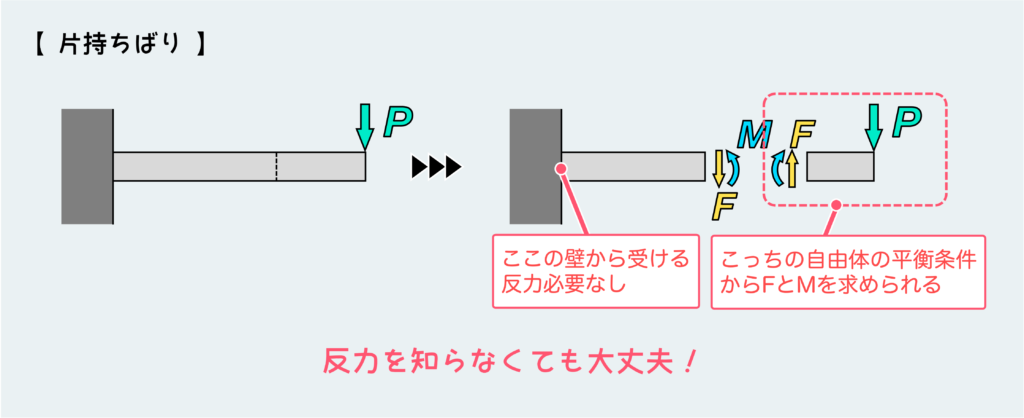
片持ちばりの場合は、適当な位置で切断してそこに働く内力を求める過程は下図のような感じになる。
この問題の場合、反力は壁から受ける力になる。しかし、はりの根本部分を切り離さない限り、この壁から受ける反力は登場しない(図に書きこめない)。しかも見ての通り、先端側の自由体のつり合いを考えることで、せん断力Fと曲げモーメントMを求めることができるので、根本側のこと(反力がどうとか)は一切考えないでいい。
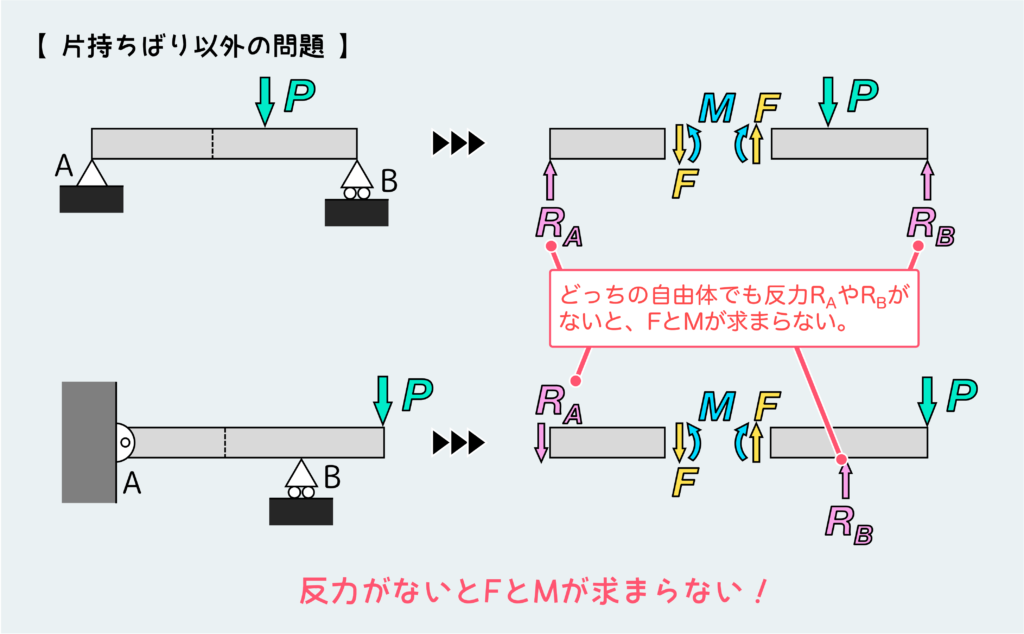
一方、片持ちばり以外の問題ではどうか?片持ちばり以外とは例えば下の絵のように、両端支持はりだったり、途中に支点があったりする問題だ。
このような問題の場合、適当な位置で切った断面に働く内力を考える過程は下のようになる。これらの場合、自由体を2つ取り出すことになるが、どちらの自由体にも未知数が3つある(内力FとM、反力R)。
この自由体の平衡条件式は2つしか立てられない(回転と上下方向のつり合い)ので、3つの未知数に対して2つの条件式ではこいつらを決定できないのである。
なので、このような問題の場合には、事前にはり全体を自由体として取り出して(支点や壁から切り離す)、反力を求めておく必要がある。
次に、場合分けが必要かどうかを検討する。簡単に言うと、はりを左端から眺めていって何か状況が変化する点があれば、そこを境に場合分けしないといけない。
場合分けが必要な状況の変化とはどういうものかと言うと、例えば下のような感じだ。
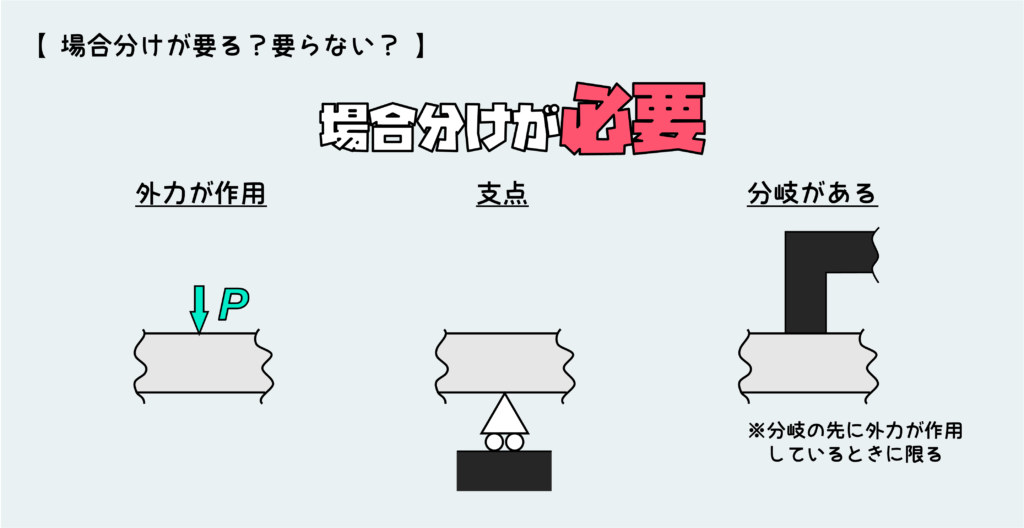
場合分けが必要なケースとはつまり、はりの途中で何か力やモーメントが作用するようなときってことだ。外力が目に見えて働いているケースは当然だし、支点がある場合もそこに反力が働く。また、分岐があるときも分岐の先に何か外力が働いていれば、それによって分岐の根本部分に力が働くことになる。
一方、場合分けが必要ないケースは下のような感じだ。

まず分布荷重に関しては気にする必要はない。よく混乱しがちなのは、材質の変化や断面形状の変化だ。これらはすごく重要な変化のように見えるが、SFDやBMDを考えるだけなら何も気にする必要はない。なぜなら、SFDやBMDは内力の変化を表すものであって、材質や形状が変わっても内力の伝わり方に影響する訳ではないからだ。
さて、では具体例でSTEP. 2をやっていこう。
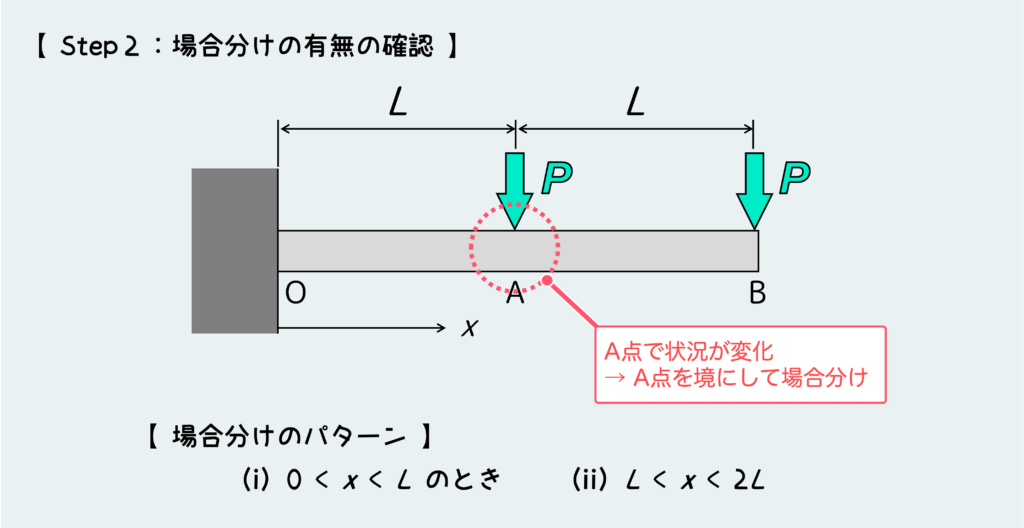
この問題の場合、中央部のA点に外力として集中荷重Pが作用している。なので、ここを境に場合分けしないといけない。つまり、パターン(i)0 < x < L と、パターン(ii)L < x < 2L の2パターンを考えないといけない。
“x” とは材料を仮想的に切る位置を表しており、それはつまり『どこの内力を考えるか』ということだ。なので、パターン(i)ではOA間に働く内力を、パターン(ii)ではAB間に働く内力を考えるってことになる。
ちなみに、xの原点(x=0)ははりの左端に設定するのがルール。
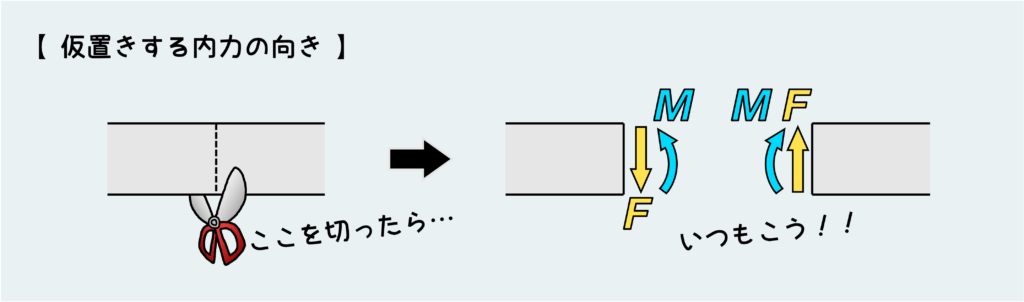
次にSTEP. 3では自由体図を描こう。ここでのポイントは、切った断面に仮置きするせん断力Fと曲げモーメントMの向きを間違えないことだ。SFDとBMDを描くときに限っては、厳密に正負の向きが決まっている。
個人的には、SFD・BMD以外のときは自分の好きな向きに仮置きすればいいと思ってるが(人によっては必ず引張を正として、引張の向きに仮置きしなさいと教える人もいるかもしれません)、SFD・BMDのときだけは決められた向きに必ず仮置きしないといけない。
仮置きするときの向きについて、こんがらがっちゃう人もいると思う。でもこれは深く考えても仕方がないので、ある断面を切ったら、左の断面にはこう!右の断面にはこう!と、機械的に描き込むようにすれば良い。
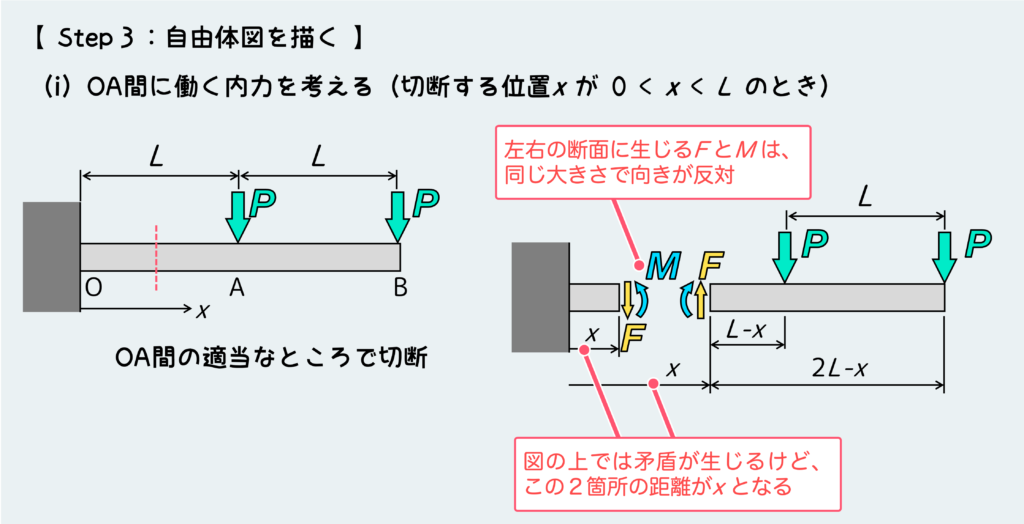
ではSTEP. 2にて場合分けをしたので、まずパターン(i)について自由体図を描こう。
OA間のどこか適当なところで切った図を描いて、切った断面にはさっき言ったようにFとMを仮置きする。
このとき、切った位置(左端からの距離)が “x” なので、これも図に書き込んでおくと良い。そうすると下図のような自由体図が出来上がる。
次に、今描いた自由体図を元に、平衡条件からFとMを決定しよう。
この問題では自由体は1つしか取り出せてないので、右側(先端側)の自由体のつり合いを考えていくが、場合によっては2つ自由体を描けるときもある。そんな時はその後の計算が簡単そうな自由体の方で、平衡条件を考えていくのが得策だ。どちらの自由体から計算していっても、出てくる答え(FとM)は同じになる。
この例では、自由体の平衡条件式は下のようになる。見ての通り、求まるFとMはxの関数として表現される。これをSTEP. 5にてグラフ上に描いていく訳だ。
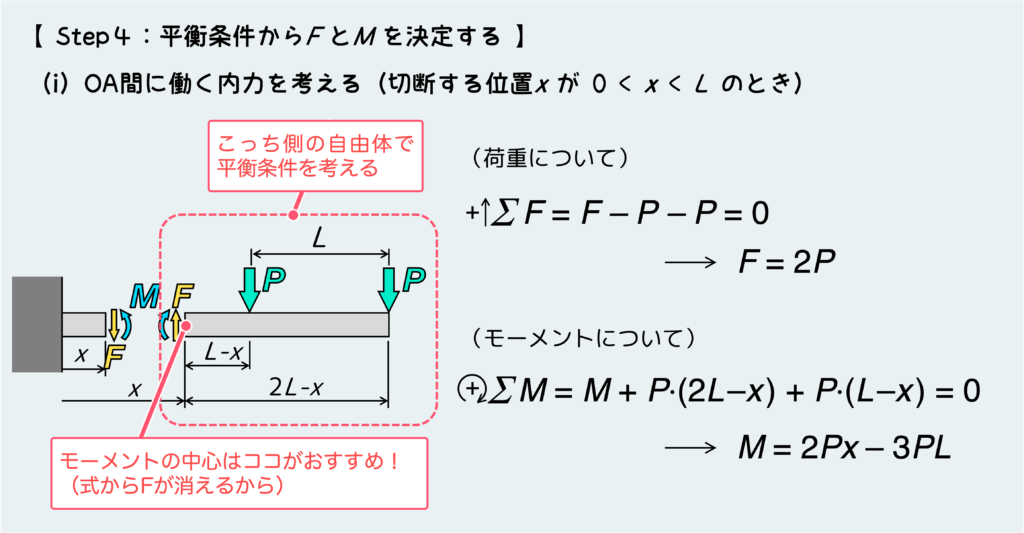
ここで1つポイントだ。回転モーメントの条件式を立てるときはどこか好きな場所に中心を設定しないといけないが、これは切った断面の位置に設定するのがオススメだ。なぜかと言うと、切断面に中心を設定することで、Fが式中に出てこなくて済む(Fにとってのウデの長さが”0″になる)からだ。
では、場合分けの2パターン目についても同様にSTEP. 3とSTEP. 4をやろう。場合分けの数だけSTEP. 3 & 4を繰り返すことで、はり上の全ての区間に対してせん断力Fと曲げモーメントMが位置 “x” の関数として求まるはずだ。
ちなみにパターン(ii)について、自由体図と平衡条件およびそこから求まるFとMは下のようになる。
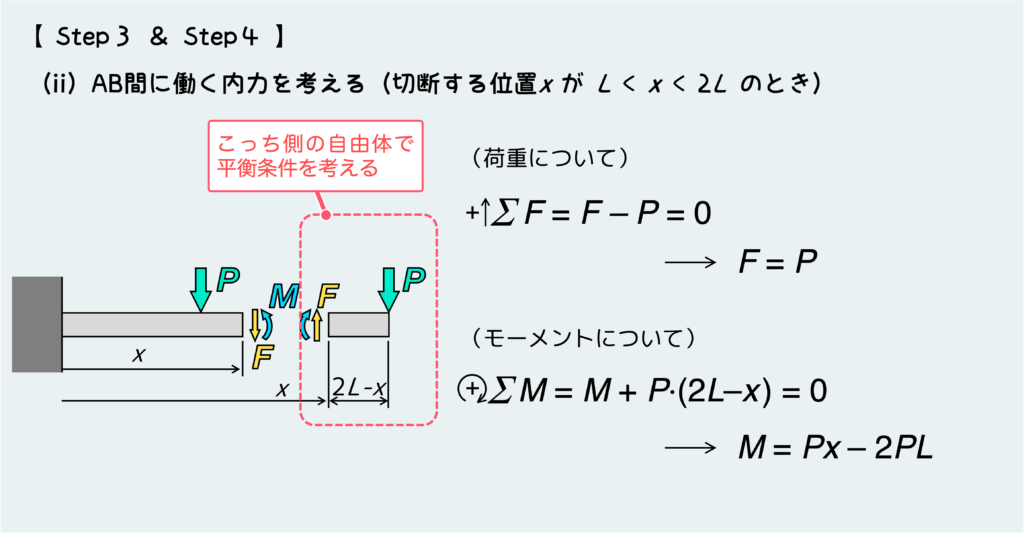
いよいよ最終STEPだ。STEP. 4までで求めたFとMをグラフ上に描いていこう。
もうこのステップに関しては、ただただ関数をグラフ上に描くだけなので、最低限の数学的知識があれば問題ないだろう。
厳密なルールという訳ではないが、節目のポイントではy軸上に具体的な数値もしくは文字を書くようにしよう。下の例では、x=L(つまり図上のA点)が節目にあたり、求めたFとMの式に対してx=Lを代入することで、その点に作用する具体的なFとMの大きさを求める。
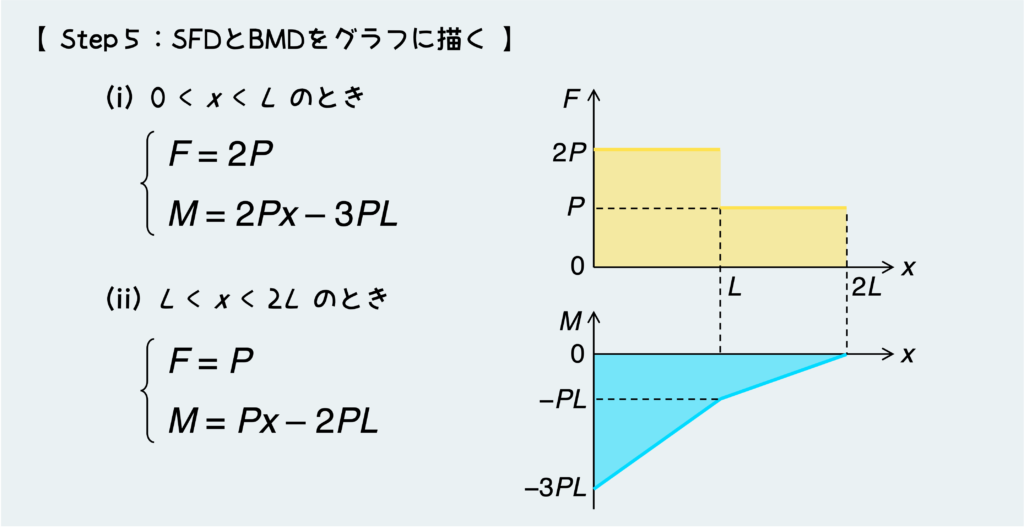
SFD・BMDでは”段”が付いたり、”角”が出来たり、特徴的なパターンが現れる。こういうグラフ上の特定のパターンは、『その部分のはりがどんな状況にあるか』に対応しているので、その対応関係を理解しておくとグラフを描き上げる上で便利だし、描いた後に間違いに気付けたりする。
このようなSFD・BMDの特徴は、次の記事で解説するのでぜひ合わせて読んでほしい。
これでSFDとBMDは完成だ!
ところで、SFDとBMDの目的は前の記事で説明した通り、どこにどんな負荷がかかるか?特に最大の負荷はどこにかかるか?を目で見て把握することにある。この例題の場合は、BMDを見れば一目瞭然、根本部分に最大の曲げモーメントが作用していることが分かる。てことは、このはりに発生する曲げ応力も根本で最大になるってことだ。
この例題はすごくシンプルなので、正直BMDを描かずともそんな事はイメージできてしまうが、複雑な問題になるとSFDとBMDを正確に描くことは、材料に発生する応力を把握する上でとっても重要になる。
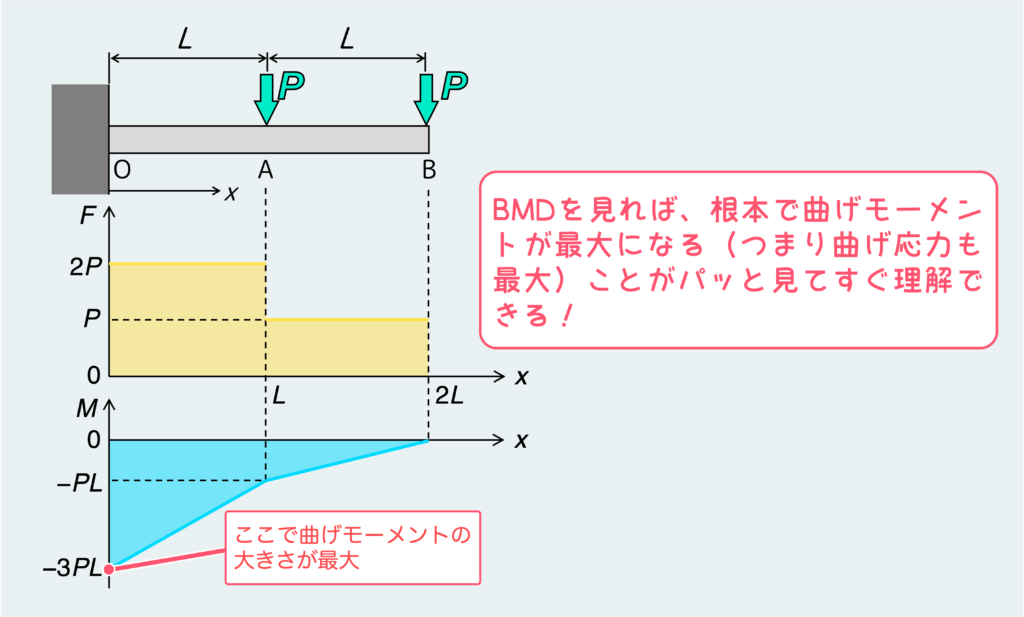
ちなみに、「根本に最大のモーメントが発生する」って言ってるけど、これマイナスじゃんって思う人もいるかもしれない。しかし、これは関係ない。曲げモーメントの正負は曲げる方向(はりの上下どちらの面に引張応力が働くか)を表すだけなので、プラスだろうがマイナスだろうが、大きなモーメントが働けば大きな曲げ応力が発生することになる。
つまり、曲げモーメントの大小を考えるときには、その絶対値に注目するようにしよう。
(※もちろん、はりの上面が下面に比べて極端に引張に弱いとか、上下で状況に違いがある場合は曲げモーメントの向きにも注意を払う必要がある。)
まとめ
SFD・BMDの描き方を徹底解説したが、この手順に沿えばどんな問題でも間違いなく描けるようになるはずだ。
あとは色んな練習問題で試してみて、描き方に慣れてほしい。
次の記事では、SFD・BMDが持ってる大事な特徴と、それによってグラフ上に現れる特定のパターンについて解説するので、ワンランクアップしたい人はぜひこれも読んでほしい。
 材料力学 SFD・BMDの押さえておきたい大事な特徴と4つの特定パターン【材力Vol. 6-3】
材料力学 SFD・BMDの押さえておきたい大事な特徴と4つの特定パターン【材力Vol. 6-3】
- SFD・BMDを描く手順は下のとおり。
- 片持ちばり以外の問題では、壁や支点から受ける反力を求めておく。
- 場合分けが必要か考える。
- 適当な所で切って(左端からこの位置までの距離を “x” とする)、自由体図を描く。
- 平衡条件から、切断面に働く内力(せん断力Fと曲げモーメントM)を求める。
- 求めたFとM(xの関数)をグラフ上に描く。


