引張圧縮の不静定問題に関する練習問題と解説にトライして、さらに考え方を身につけよう。
今回の難易度は「 」です。
夢へ駆ける少女の姿に感涙！！
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか？」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい！」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanなら2/4までなんと3巻無料で読めてしまいます！まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです！
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
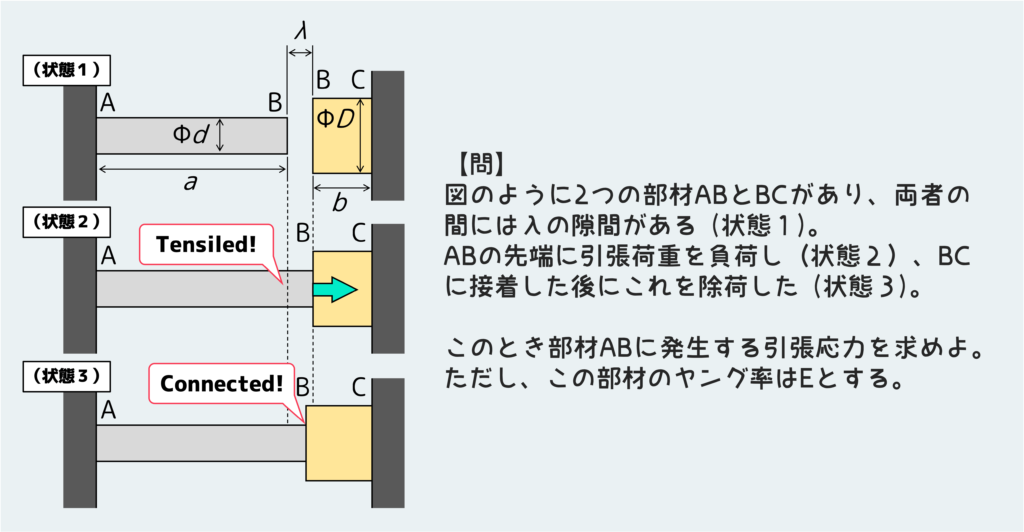
この材力練習問題を解く上でのポイント
今回の問題を解く上でのポイントは以下の通りだ。
- 外力がないときも状況から正しく自由体図を描けるか？（内力を把握できるか？）
- 変形の条件を正しく見極める
ポイントが理解できていないと感じる人は以下の記事を読んでみてほしい。
材料力学 《全員必見・超重要》自由体の考え方の基礎【Vol. 1.1】
材料力学 《全員必見・超重要》自由体の考え方（引張・圧縮を受ける棒）【Vol. 1.2-1】
材料力学 引張・圧縮を受ける材料の不静定問題【Vol. 3-3】
この材力練習問題の解き方
この問題の大きなポイントは、『考えるべき状態（状態３）において外力が存在しないこと』である。
通常は構造体のある点に外力が作用しており、そこを起点にして内力の伝わり方を把握していく（自由体図を描く）のだが、この問題ではそのとっかかりになる外力が存在しない。
外力が働いていないってことは、この材料には何の負荷もかかってないってことだろうか？
当たり前だけど、そんな訳はない。何かしらの負荷を受けた状態になっているはずである。（じゃないと問題として成立しないよね）
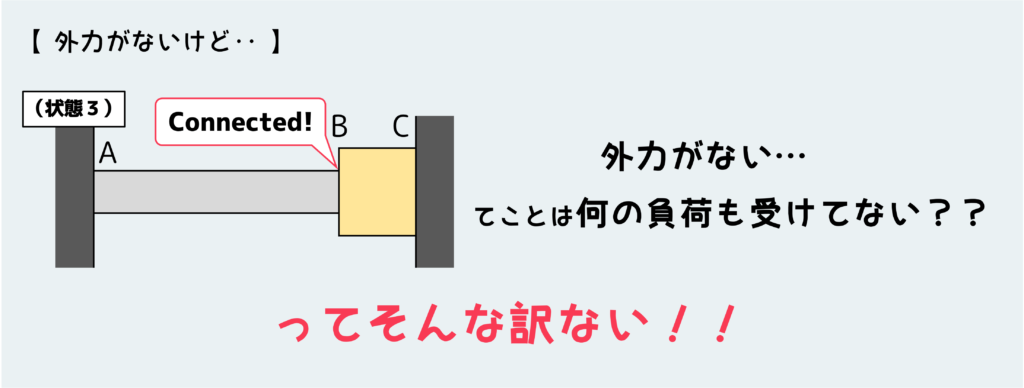
では、この材料はどんな負荷を受けた状態になっているだろうか。
これを理解するためには、言うまでもなく材料の状態をイメージすることがとっても大事だ。
材力は基本的には機械部品のようなものを想定しているが、考え方の本質は日常で起きていることにも適用できる。身近なもので同じような状況を想像してみることは、材力の問題を解く上で極めて重要なことだ。
さて、今回の問題も日常の中にあるものでイメージしてみてほしい。
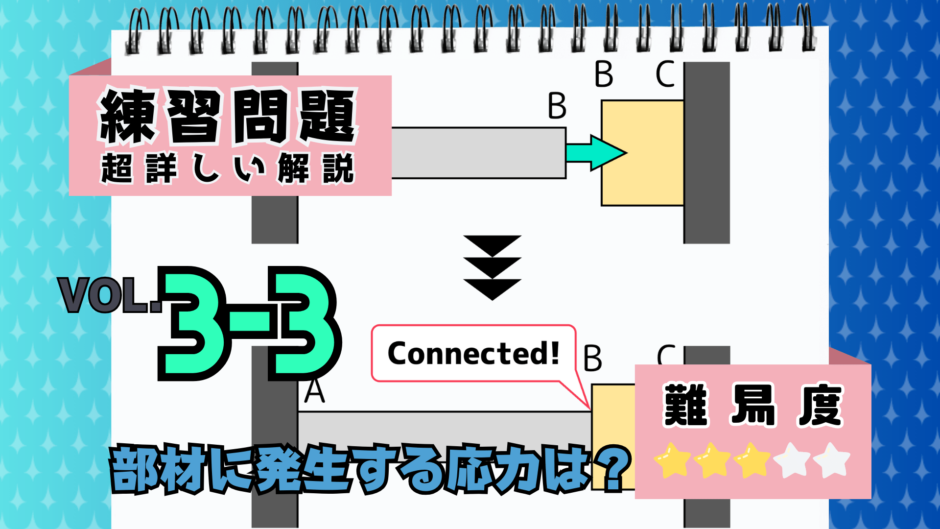
２つのゴムを用意し、一方のゴム（下図：灰色）をグーっと伸ばしてきて、もう一方のゴム（下図：黄色）に接着する（下図：状態２）。この時点では、一方のゴム（灰色）に引張負荷が作用しており、このゴム（灰色）が伸びているだけである。その後、引っ張っていた手を離す（下図：状態３）。そうすると、引っ張ってきたゴム（灰色）は少しだけ縮むと同時に、もう一方のゴム（黄色）は縮むゴム（灰色）に引っ張られて少し伸びる。
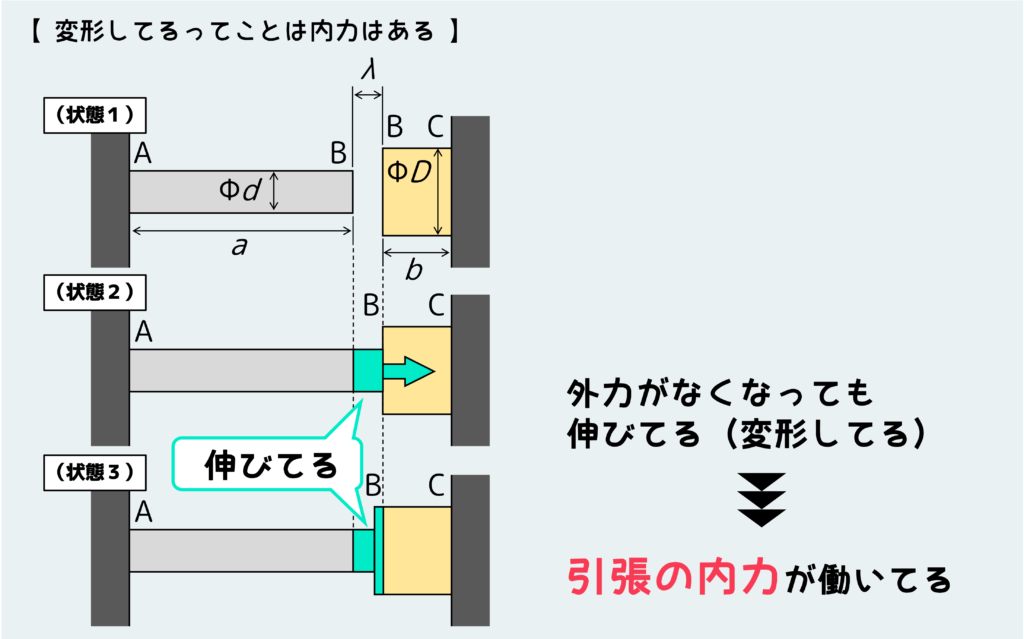
てことは、最終的な状態としてはゴムは２つとも初期状態よりも伸びている状態にあるということだ。
伸びている（変形している）ということは何かしらの負荷が作用している状態であり、この場合はそれは引張の内力だと言える。
つまりこの問題では、２つの部材がお互いを引っ張りあっている状態になっている訳だ。
このようにたとえ外力がなかったとしても、状態によっては内力は存在している。
材料の状態をイメージすることが重要！！
どんな問題もそうだが、シンプルな形というか、それぞれの負荷形態における基本形の組合せに問題を置き換えることが大事だ。
複雑そうに見える問題ほどシンプルな状態の組合せに置き換えて、一個ずつ丁寧に解いていく必要がある。
今回の問題も、下図のような引張圧縮問題におけるシンプルな形に分解して考えていく。
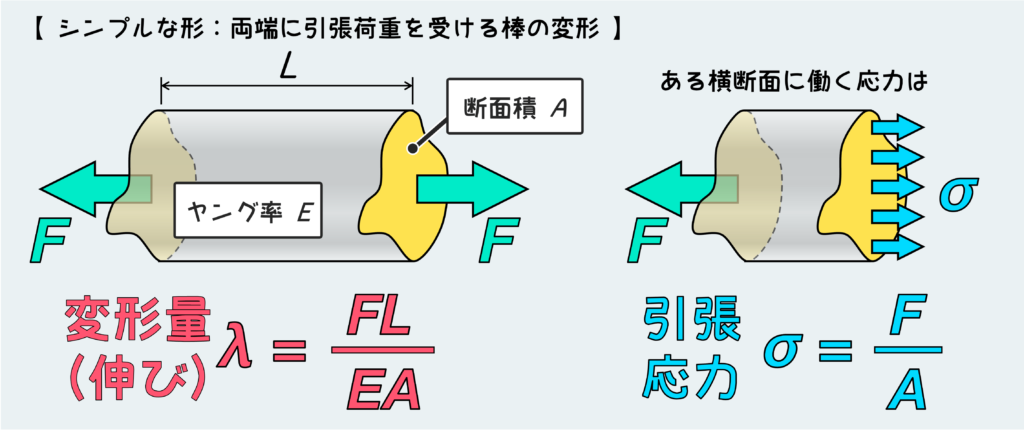
両端に引張荷重を受ける棒の変形と、ある横断面に働く応力は上のように表せる。
ヤング率Eは材質によって決まるもので、断面積や長さは材料の寸法で与えられるものなので、重要なことは荷重Fを正しく見極めることだ。
何度も言っていることだが、『自由体の考え方』を使って内力の伝わり方を把握すれば、この荷重Fを正しく見積もることができる。
部材ABと部材BCが両者ともに伸びている＝引張の内力を受けているということを踏まえて、自由体図を描いていこう。
両部材に働く引張力をそれぞれF1とF2と仮定すると、下図のようになる。（ついでに壁も部材から引っ張られるので、これをRAとRBとする）
さらに、作用・反作用の法則を考えると壁と部材同士、部材ABと部材BCはお互いに引っ張りあっているため、両者の間に働いている引張力は等しい大きさである必要がある。
結果として、下のように壁、部材AB、部材BCすべて同じ大きさの引張力Fを受けている状態だということが分かる。
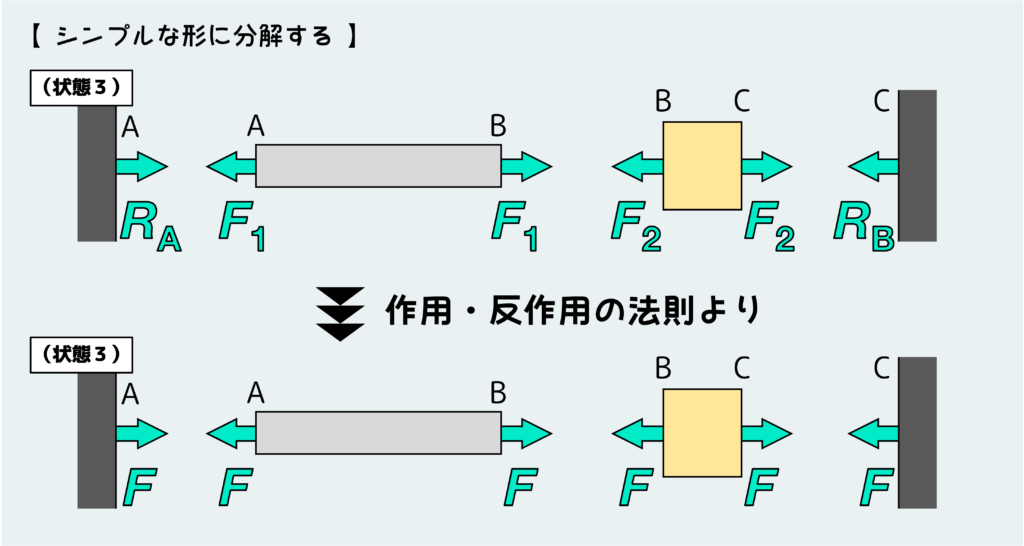
これで自由体図としては完成なのだが、この時点では引張の内力Fを決定することができない。
つまりこの問題は不静定問題であり、この引張力Fの大きさを決定するためには『変形の条件』が必要になる。
『変形の条件』を見極めるためには変形の様子をイメージすることが大事だ。
コツは『他の部分がどうなるかはまだ分からないけど、絶対にここはこうなる』というポイントを見つけることだ。
今回の問題では下図のようになるので、二つの部材は両方ともに伸びている。この伸びの大きさ自体はまだ現時点では分からないが、２つの伸びの合計が最初の状態の隙間λと等しくないといけない。
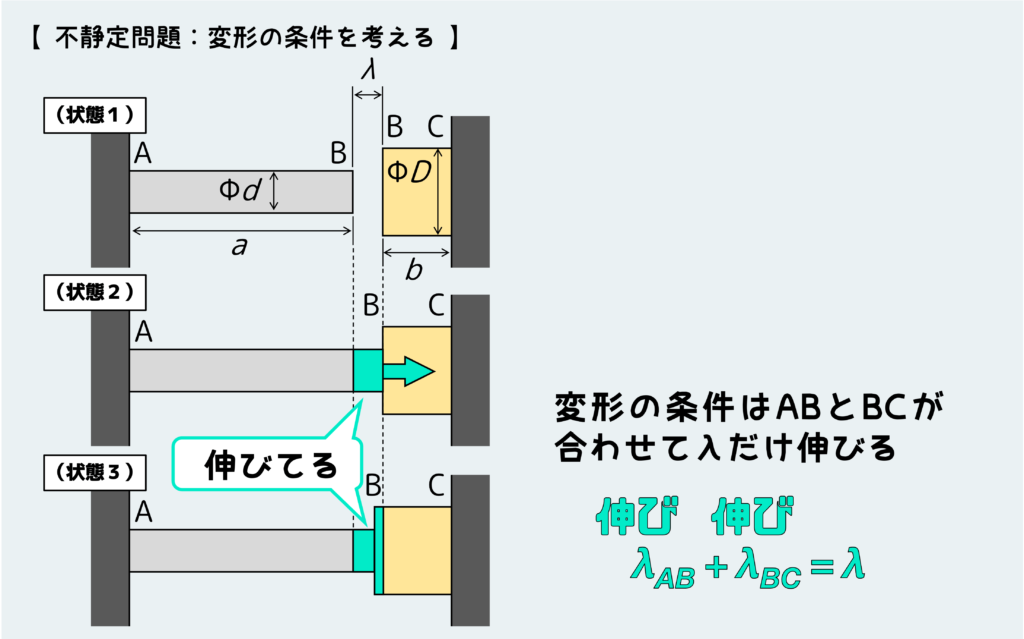
したがって、この問題の『変形の条件』はλAB+λBC=λ となる。
『変形の条件』が分かったら、仮置きしている内力Fを使って条件式化する。
公式を使って各部材の伸びは下のように表せるので、これらを『変形の条件式』に組み込むと、Fに関する条件式が出来上がる。
あとはこれを式変形すればFの大きさが求まる訳だ。
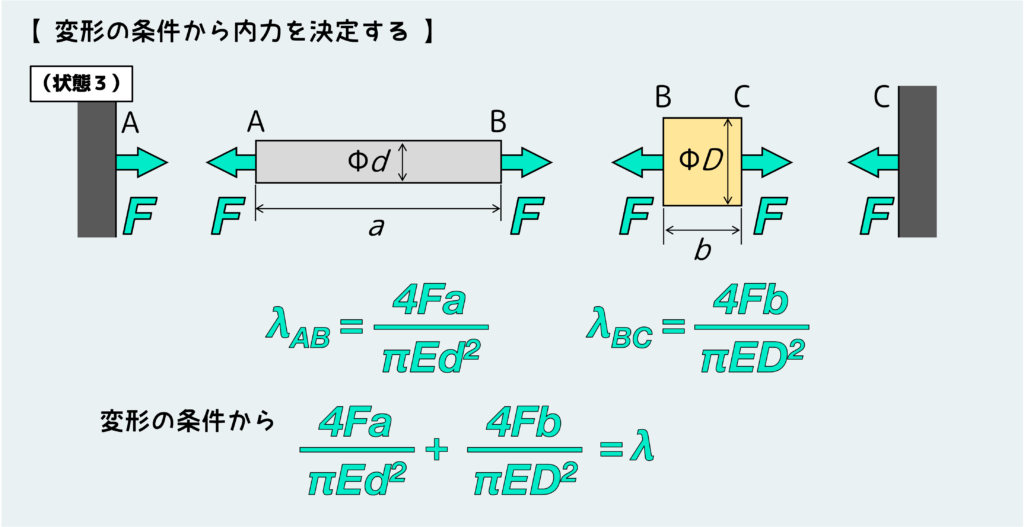
内力が把握できさえすれば、この問題の全体像がつかめたと言える。
ここまで来れば、何を聞かれても対応できる。質問に合わせて、内力をもとにして計算すればいいだけである。
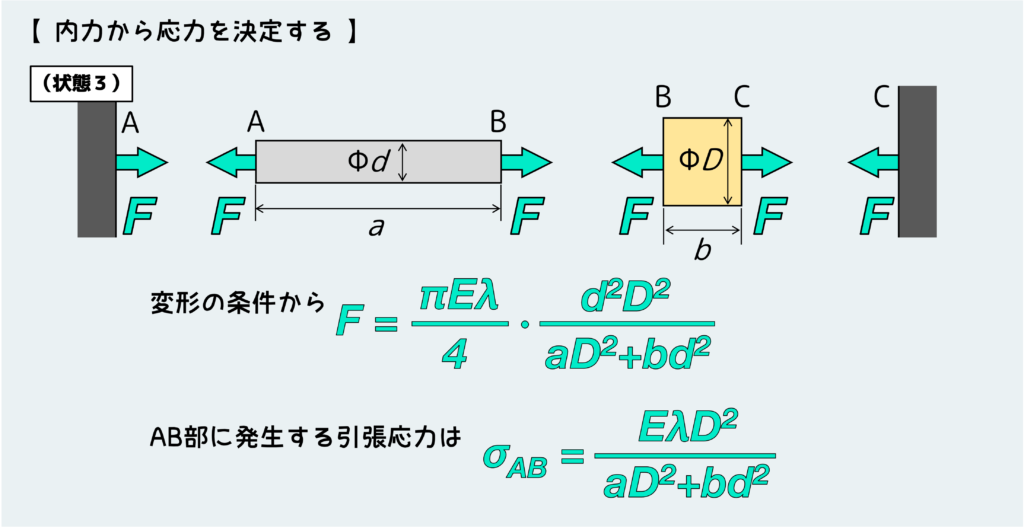
今回は部材ABに働く引張応力を聞かれているので、さっき求めた内力Fを断面積で割れば良い。
したがって、この問題の答えは下図のように求まる。
類似の材力練習問題
今回と同じく引張圧縮に関する問題を以下にまとめているので、他の問題にもチャレンジしたい人は見てみてほしい。
引張圧縮に関する復習
引張圧縮に関してめちゃくちゃ分かりやすく解説した記事たちはこちら。
改めて基礎を確認したい人は以下の記事を読んでみてほしい。
理工系人材必読の超おもしろ漫画！！
連載中
『まずは音を出して 音を出さなきゃ音楽は始まらないのよ』
今、忘れかけていた夢への一歩を踏み出す！
いつの間にか多くの人は昔描いた夢のことを忘れてしまう。『宇宙兄弟』は“夢を追うのに遅すぎるなんてことはない”ということを教えてくれます。キャリアや進路に悩むすべての人の背中を押してくれる言葉にあふれている『宇宙兄弟』は多くの社会人や大学生から大絶賛されています。
宇宙開発や飛行士の活動をリアルに描く本作は、理工系の人の知的好奇心を刺激し、未知の問題へ向き合う姿勢を学べる必読書と言っても決して過言ではありません！
ebookjapanなら3巻まで無料で読めるので、気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
![[thumbnail]_Vol1-1en](https://secondinspire.com/wp-content/uploads/thumbnail_Vol1-1en-min-160x160.png)