自由体図を描くことの重要性は前の記事で散々説明してきたが、描くだけではもちろん終わらない。
つまり、描いた自由体図を元に平衡条件式を正しく考えないと、内力が決定できないので意味がないという訳だ。
そこでこの記事では平衡条件式を正しく考える方法を解説したいと思う。超基本的な内容なので、あまり特別なことは書いてないが、一度目を通しておいてほしい。
- とにかく「力」と「モーメント」の合計が “0” になるように式を立てる。
- トラスの問題でピンの平衡条件を考えるときには、「ベクトル和 = 0」の考え方を使うと便利!
- ある面に働く内力を考えるために、切断して2つの自由体ができる場合、どちらの自由体を使って平衡条件を考えても良い。
- 力によるモーメントを考えるときには「腕の長さ」の取り方に注意。
- すでにモーメントとして存在しているものは、「腕の長さ」「中心の位置」に関係なく、そのままの形で式に入る。
- 分布荷重を考える際は、集中荷重に置き換えて考える。
とにかく力と回転モーメントの合計が”0”になるように式を立てる
平衡条件は「力」と「回転モーメント」の2種類の平衡を考える必要がある。それぞれ見ていこう。
力の平衡条件については、ある方向の力の合計が”0″になる必要がある。二次元問題の場合は、左右方向と上下方向の2方向それぞれで力の合計を考える。三次元問題の場合は、x方向、y方向、z方向の3方向で力の合計が”0″になることを考える。
力については特に注意することはない。漏れなくすべての力を式に入れること。これに尽きる。
強いて言えば力の方向にしっかり注意して、自分の定めた正負のルールに従って式に入れることだ。
モーメントの平衡条件は、2次元問題の場合ある1点を中心にしたモーメントの合計が”0″になるように式を立てる。3次元問題の場合は、3つの独立する軸に関するモーメントがそれぞれ”0″になる必要がある。
いずれにしてもモーメントを考える際の支点(2次元のときは中心とする点、3次元のときは中心軸)の位置は自由に設定することができる。
基本は以上だ。別に難しいことはないと思う。
以下では、いくつか気を付けるべき・知っておくべきポイントについて説明したいと思う。
トラスの問題ではベクトル和を考えると便利
力の平衡条件を考える場合、「ベクトル和」という考え方を利用すると便利なことがある。この考え方は、ある1点の平衡条件を考えるようなときに使える考え方なので、特にトラス問題で活躍することが多い。
トラス構造については別の記事で詳しく説明したいところだが、とにかく長い棒をすべてピンで接続したような構造だ。【ピン接続】というのがミソで、ピンは回転自由でモーメントを伝えることができないので、各部材には軸力(部材の長手方向に沿った引張もしくは圧縮の力)しか作用しないことになる。
各部材に働く軸力を求めるやり方として「節点法」というのがある。部材とピンをすべてバラバラに切り出して自由体とし、ピンの平衡条件から各部材に伝わる軸力を求める方法だ。このピンの平衡条件を考えるときに「ベクトル和」の考え方が使える。
以下のような具体例を見ながらやり方をマスターしよう。
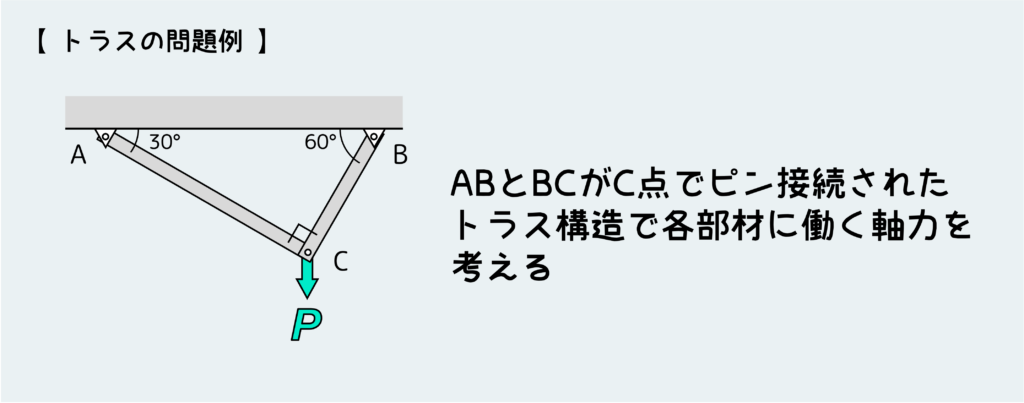
まず部材とピンを自由体としてバラバラにする。部材には軸力しか働かないので、ピンと部材の間に働く内力の方向は決まっている。
ピンの平衡条件を考えることで、各部材に働く力を決定できる訳だ。
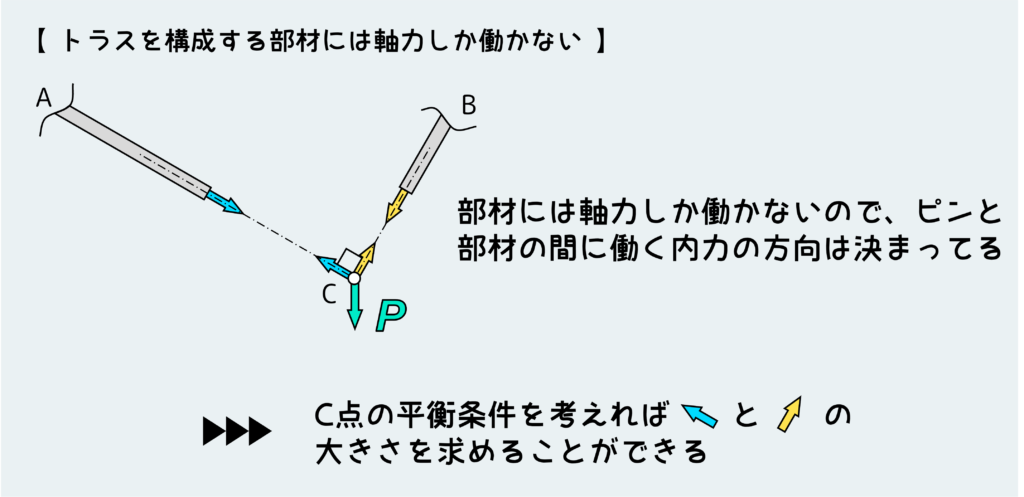
ピンの平衡条件を考える際に、ベクトル和の考え方が利用できる。ベクトル和が0になるということは、力の平衡条件が成り立つことを意味している。
ピンは、つまり点なので、モーメントのつり合いを考える必要がない(常に成り立つ)。という訳で、このピンの平衡条件を考えるときには、 “ベクトル和=0”を考えるだけで済む。

さて、ここでベクトル和とはどんな風に考えるのだろうか。
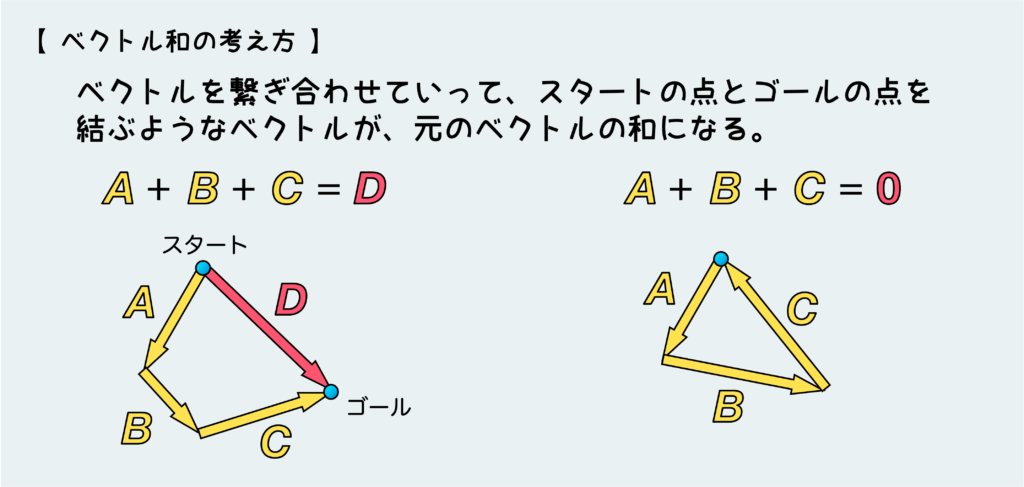
ベクトルを足していくということは、矢印を繋ぎ合わせていくってことである。下の例のようにA、B、Cという3つのベクトルがある場合、ABCの矢印(ベクトル)を繋ぎ合わせていき、その繋ぎ合わせたもののスタートとゴールを結べば、ABCを足し合わせたベクトル(D)が出来上がる。
てことはベクトル和が ”0” というのは、この繋ぎ合わせていったもののスタートとゴールが一致するということだ。こうなると、足し合わせたベクトルが ”0” ということになる。つまり下図の右のようにぐるっと元の点に戻ってくるような絵を描ければ、これらの足し合わせたベクトル和が ”0” ということだ。
じゃあ、この例題においてベクトル和が ”0” になるような絵を描いてみよう。
ピンCに働く3つの力の方向は決まっているので、あとはこれら3つのベクトルの大きさをうまく調整して、元の点に戻ってくるようなベクトル和の図を描いていく。
そうすると右下のような三角形が描けることにになる。
ここでのポイントは図をきれいに描くことだ。この考え方は式を使わずに、図形の上で幾何学的に解く方法なので、図が汚いと話にならない。きれいな図を描けば、三角形の辺の比率から自ずとFACとFBCの大きさ(三角形の辺の長さ)がわかる。
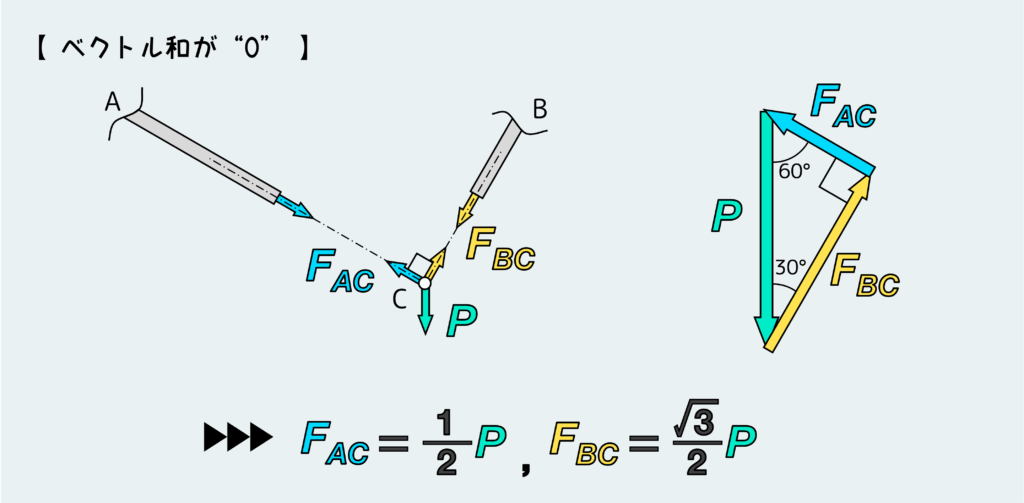
上の例では、1:2:√3の三角比から、FACとFBCの大きさが求まる。外力Pとの関係がこのようになったときにベクトル和が ”0” になる、つまり力のつり合いが取れた状態になる。
トラスの問題は特にそうだが、材力においてきれいな図を描くことは非常に重要だ。きれいな図を描ければ、このようにサッと平衡条件を考えることができたりする。
もちろんこの問題の場合、ベクトル和の考え方を使わずに、水平方向の力のつり合いと鉛直方向の力のつり合いを条件式として作って、その2式で連立方程式を解いても良い。
だがはっきり言って、ベクトル和を使ったほうが楽だ。ぜひトラスの問題では、ベクトル和の考え方を使ってスマートに解き進めるようにしてほしい。
切り出した自由体のどっちを使ってもいいんだよ
次に、構造体のある面で切断して自由体が2つできるような例を考えよう。
こんな時は、上の見出しに書いてる通り、2つの自由体のどちらを使って内力を考えても問題ない。
下のような例題を考えよう。
例えば2つの材料が接着された構造になっており、この接着面での破壊が心配なのでここに働く応力を考えたい、みたいな状況だ。このときはもちろんこの接着面で切断して、そこに働く内力を求める必要がある。
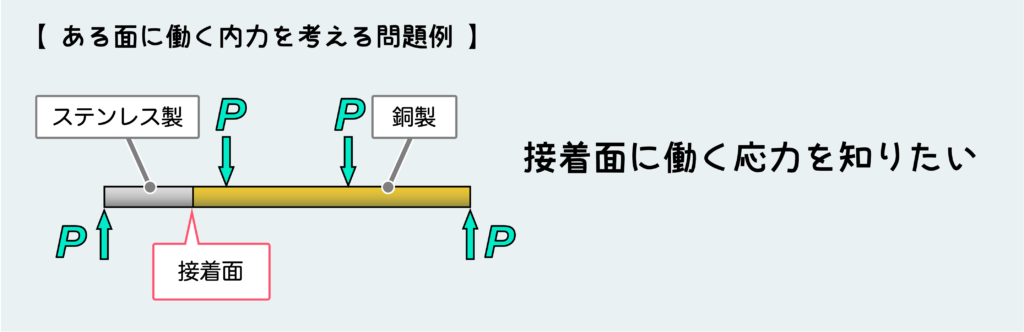
接着面で切断して自由体として取り出すと下図のようになる。
今切断した面に内力を描き込んでいるが、左右の切断面に働く内力は作用・反作用の関係にあるので、同じ大きさで反対向きの内力が働いている。
なので、この2つの自由体のどっちを使って平衡条件を考えても、出てくる答え(切断面に働く内力、ここではFとM)は同一のものが出てくる。
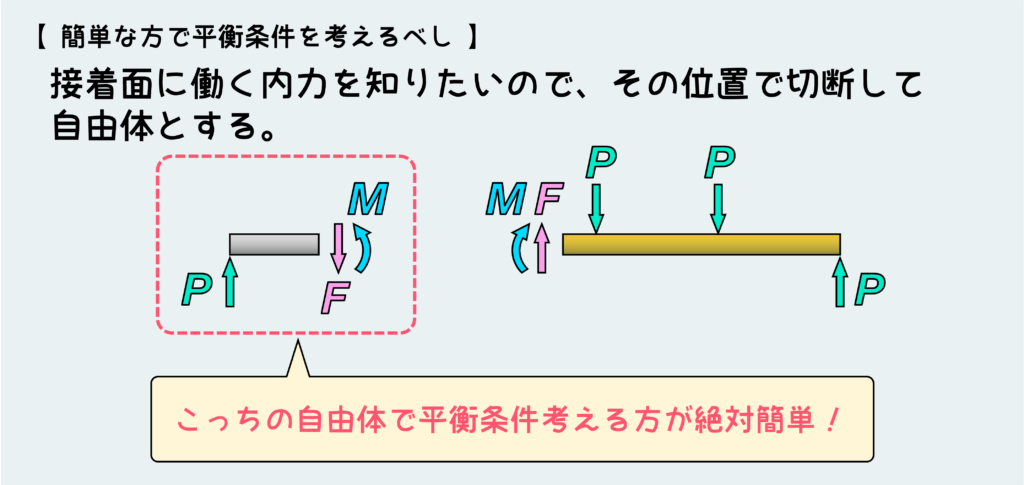
それなら労力が少ない方でやろうよ、ってことである。上の例で言うと、どう考えても右の自由体で平衡条件を考えるよりは、左の自由体で考えた方が楽だろう。
ここでは、ある面に働く内力を考える必要があるシチュエーションの問題をわざわざ例に出したが、はりの曲げ問題なんかでSFD・BMDを考えるときにもこの考え方は使えるのでしっかり理解しておこう。
回転モーメントの平衡条件を考える時の注意点
最後に、回転モーメントの平衡条件を考える時にミスしがちな点について、いくつか紹介しておこう。
下図のような問題の、回転モーメントの平衡条件を考えてみよう。
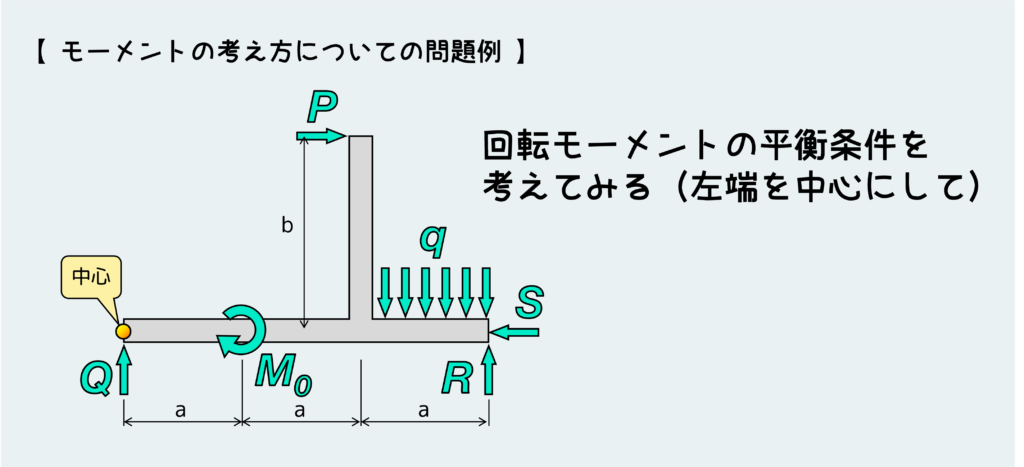
まず1つ目の注意点は、力によるモーメントを考えるときの「腕の長さ」の取り方についてだ。
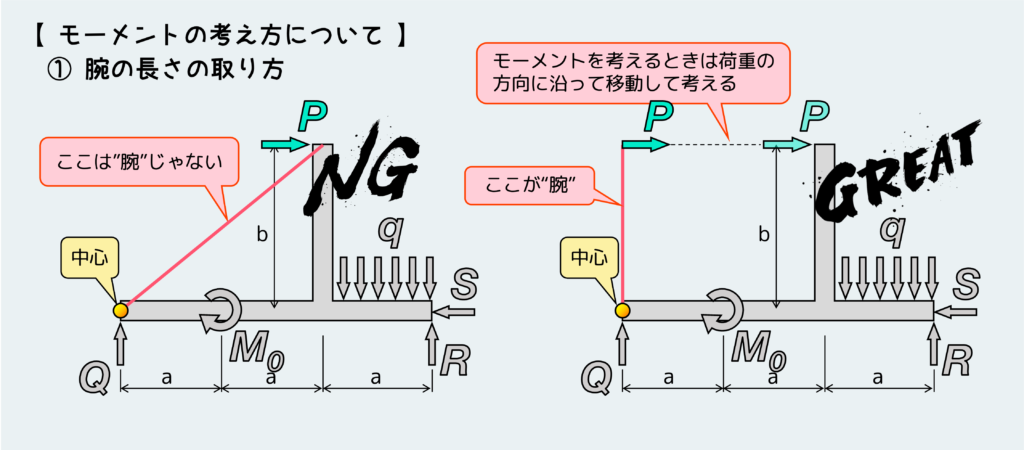
この例題で、左端の点を中心にモーメントを考える場合、外力Pに対する腕の長さは斜めにとってはならない(左下図)。力によるモーメントを考える際、必ず腕の部分と力は垂直になっていないといけない。
なので、正しくは右下図のように、腕と直行する位置まで力を移動して考えないといけない。
次に、力によるモーメントではなく、すでにモーメントとして存在しているものの取り扱いについてだ。
下図のように、ある点にモーメントM0が作用しているときに、これを平衡条件式の中ではどう扱えばいいか?
たまに勘違いしている人がいるが、力によるモーメントを考えるときと違って、すでにモーメントとして存在しているものについては”腕の長さ”とか考える必要はない。モーメントはそのまま平衡条件式に登場する。ここで注意すべきは、どこを中心に設定して式を作っても、モーメントはそのままの形で式に組み込まれるということだ。
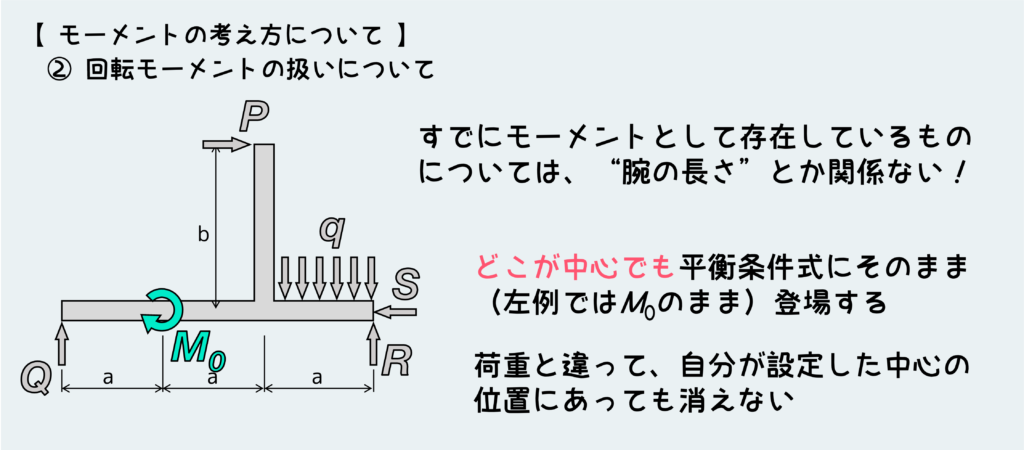
この例で言えば、左端の点を中心に式を作ってもM0がそのまま式に入るし、M0が作用している点を中心に設定しても同じくM0がそのまま入る。
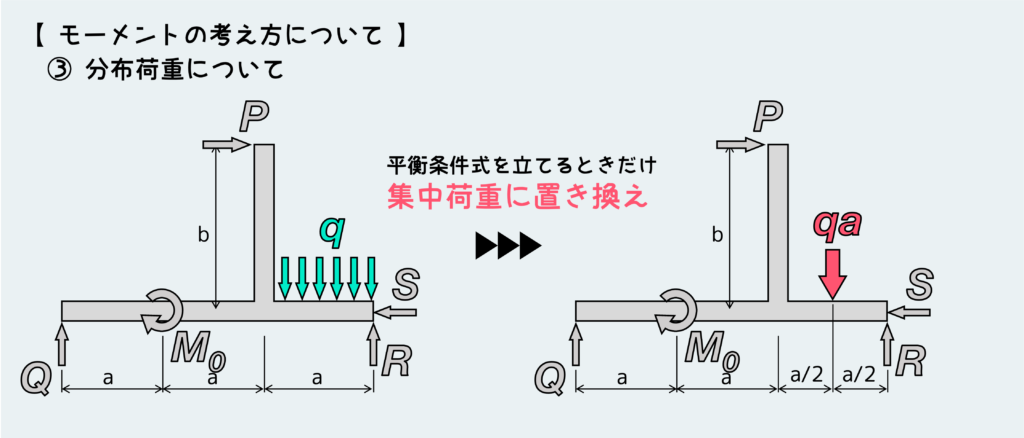
最後に分布荷重の取り扱いについてだ。
この例題のように一定の分布荷重が作用している場合は、集中荷重に置き換えて平衡条件式を立てることができる。
置き換える集中荷重は、分布荷重が作用していた部分の中心位置に作用しているものとして考える。
まとめ
平衡条件の考え方について説明してきたが、理解できただろうか?
材料力学の問題を解く上で、『自由体図を描く』そして『平衡条件を考える』ことはほぼほぼすべての問題のスタート地点だ。この2つをしっかりできるようになれば、材力の問題を解くのはそこまで難しくはない。
なので、今回紹介したことをしっかり理解して、使いこなせるようになってほしいと思う。
- とにかく「力」と「モーメント」の合計が “0” になるように式を立てる。
- トラスの問題でピンの平衡条件を考えるときには、「ベクトル和 = 0」の考え方を使うと便利!
- ある面に働く内力を考えるために、切断して2つの自由体ができる場合、どちらの自由体を使って平衡条件を考えても良い。
- 力によるモーメントを考えるときには「腕の長さ」の取り方に注意。
- すでにモーメントとして存在しているものは、「腕の長さ」「中心の位置」に関係なく、そのままの形で式に入る。
- 分布荷重を考える際は、集中荷重に置き換えて考える。




