このブログには「広告」を含む記事があります。
今回の記事では、いよいよトラスの変形問題について解説したい。
変形の考え方は『エネルギー法』や『カスティリアーノの定理』を使う方法とかもあるが、今回は『幾何学的な考え方』について説明する。
比較的シンプルな構造のトラス問題を考える際に幾何学的に解くのだが、まあこれがよく分からない学生は多いと思う。教科書の説明が不親切というか足りないことが原因だろう。
そこでこの記事では、トラス変形問題の幾何学的な解法についてめちゃくちゃ丁寧に解説する。少し長くなるが、絶対分かるようになると思うのでぜひ最後まで読んでほしい。
ちなみにトラスの力の伝わり方(節点法)と(切断法)については下の記事にまとめているので、興味がある人はこちらも読んでみてほしい。
 材料力学 10分で絶対分かるようになるトラス問題(節点法による力の伝わり方編)【Vol. 3-4】
材料力学 10分で絶対分かるようになるトラス問題(節点法による力の伝わり方編)【Vol. 3-4】
 材料力学 10分で絶対分かるようになるトラス問題(切断法による力の伝わり方編)【Vol. 3-5】
材料力学 10分で絶対分かるようになるトラス問題(切断法による力の伝わり方編)【Vol. 3-5】
- トラスの変形を考える上で重要なのは、各部材が回転することの意味をしっかり理解すること。
- ある節点は、その節点につながっている部材すべての変形が同時に成り立つような点に移動する。
- Step 1:部材に働く力を求める。
- Step 2:各部材の個別の変形量を求める。
- Step 3:各部材の変形させた図を描き、その先端から部材に垂直な線を引く。
- Step 4:部材それぞれから垂線を引いたら、これらの交点が節点の移動先。
- Step 5:図から三角比などを利用して、節点の移動量を計算する。
Contents
トラスとは
トラスとは下の絵のような構造体で、ポイントはすべての部材がピン接続されていることだ。
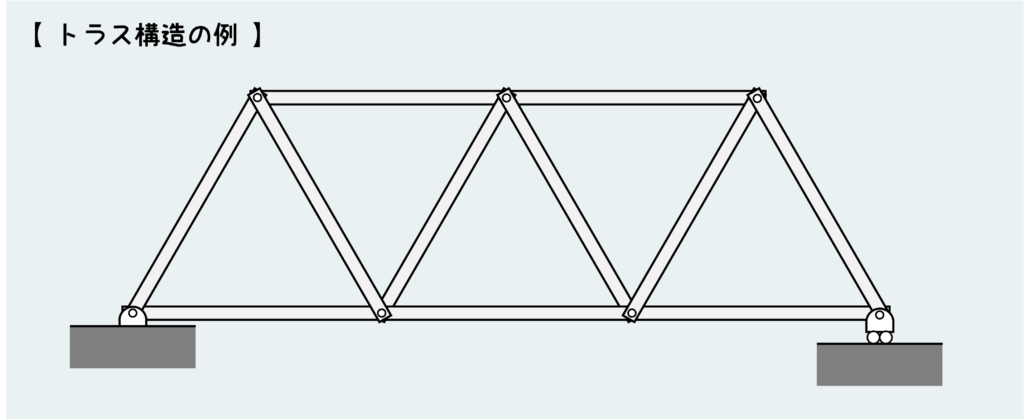
ピン接続というのは『部材同士が離れないように拘束している一方で、部材同士の回転は拘束しない』という特徴がある。これはつまりどういうことか言うと、『力を内力として伝えることができるが、モーメントは伝えられない』ということである。
これがピン接続の大きなポイントだ。
その結果、トラスを構成する部材には軸力(長手方向の力)しか働かないというめちゃくちゃ重要ポイントが生まれる訳だ。これがトラス問題の大前提なので、しっかりと押さえておこう。
トラスの変形の考え方
では例題に入る前に、基本的な考え方を説明しておきたい。
まず前回説明した節点法を使って各部材に働く力を明らかにしておく。節点法を使うためには、全部の部材とピンをバラバラにして、自由体のつり合いから内力の伝わり方を把握していく。
 材料力学 10分で絶対分かるようになるトラス問題(節点法による力の伝わり方編)【Vol. 3-4】
材料力学 10分で絶対分かるようになるトラス問題(節点法による力の伝わり方編)【Vol. 3-4】 各部材に働く内力がわかったら、これを元にそれぞれの部材の変形量(伸び・縮み)を計算する。これはただただ公式を使えばいい。
各部材がバラバラに変形したとしたときの先端の移動先を描き、この点から部材に対して垂線を引くと、この線が「この部材の先端が移動し得る位置」になる。
すべての部材で垂線が引けたら、各部材の変形がすべて成り立つ点はこの垂線の交点しかないので、ここが最終的な移動先となる。
あとは図を元に三角比を利用して、移動量を計算すればいい。ここでのポイントは図を丁寧に描くことだ。
以上の手順を踏んでいけば、簡単に解けるはずだ。
次に例題を見ながら、もう少しこの手順でやっていることの意味を解説していこう。
簡単な具体例
では下図のような超単純な例を使って、上で説明した手順の意味について理解しよう。
この問題では2つの部材ABとCBがあり、節点Bの変位を求めてみよう。
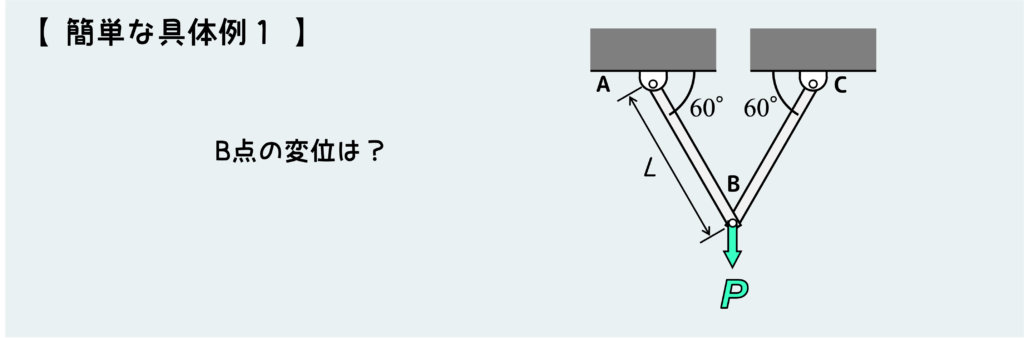
まず節点法を使って、各部材に働く力を求める。節点法のポイントは各部材をすべてバラバラに分解して、自由体のつり合いから各部材に伝わる内力を求めていくことだ。
 材料力学 10分で絶対分かるようになるトラス問題(節点法による力の伝わり方編)【Vol. 3-4】
材料力学 10分で絶対分かるようになるトラス問題(節点法による力の伝わり方編)【Vol. 3-4】
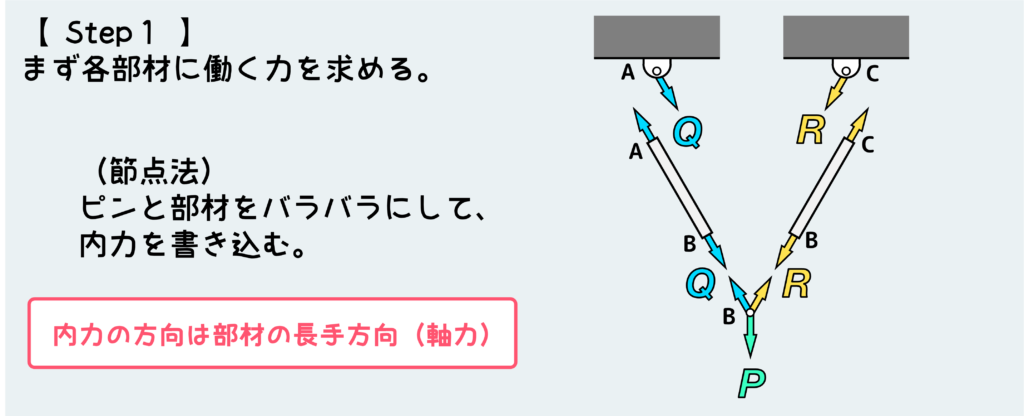
この問題では、節点Bのつり合いから、各部材に働く内力QとRを求める。
節点(ピン)のつり合いを考える時は下図のように「ベクトル和=0」の考え方を使うと簡単なことが多い。(いつも言っていることだが、図をきれいに丁寧に描くことが大事だ。)
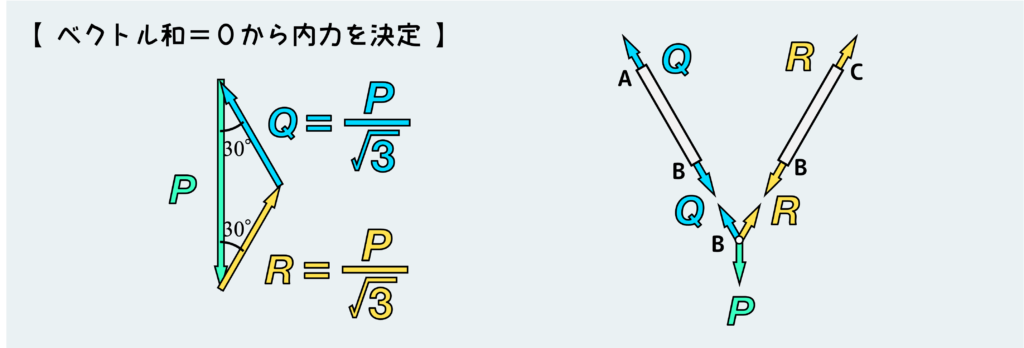
各部材に働く力が求まったら、それぞれの部材の変形量(伸びや縮み)をあらかじめ計算しておく。
この計算は公式を使えばいいだけだ。
部材の断面積、ヤング率(縦弾性係数)、長さとさっき求めた内力が分かっていれば、公式から変形量が計算できる。
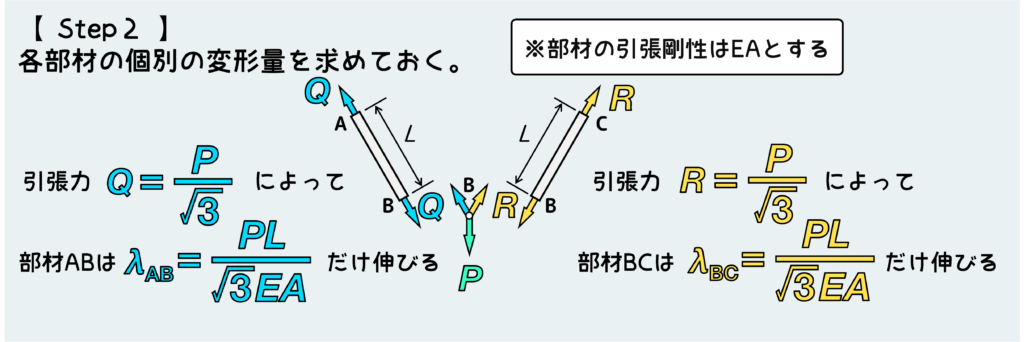
さて、これで準備が整った訳だが、この例題を解き進める前にこの解法の根幹となっている考え方について説明しておこう。
トラスの大前提だが、各部材がピンで接続されているので各部材は回転することができる。このことがとても大事だ。
下図のようにまず単独の部材の動きを理解しよう。部材ABがλABだけ伸びるときにこの先端の点(B1とする)はどこに動き得るかというと、下図で青破線で描いた線上のどこかになる。
このように固定端(実際には固定されていなくてもよくて、どちらかを仮想的に固定して考える場合もある)を中心にして、円周上のどこかの点に先端が移動する。これを理解することが正解への第1歩だ。
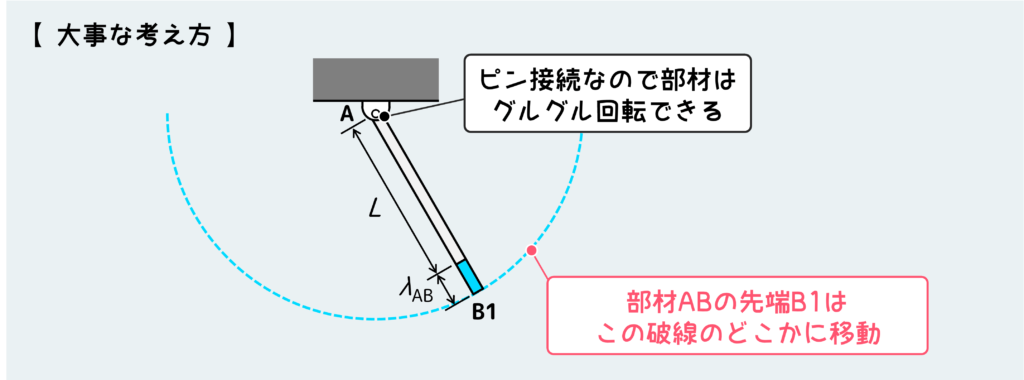
実際には別の部材が繋がっているので、今変位を求めたい節点(今回はB点)に繋がっている全ての部材の変形を同時に考えないといけない。
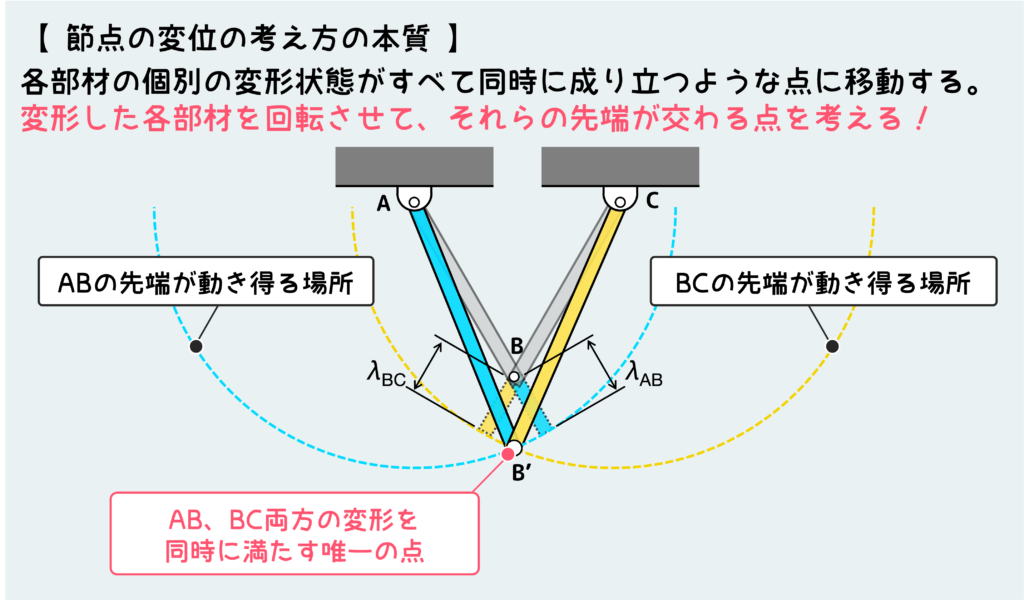
先ほど説明した単独部材の変形の考え方を他の部材にも適用して、同時にすべての変形が成り立つように考えると下図のようになる。
部材ABの先端は青破線上のどこかに移動する必要がある。これと同時に部材CBの先端は黄色破線上のどこかに移動する必要がある。
すなわち、両方の部材の変形を同時に満たす場所=2つの破線の交点が節点Bの移動先として決定できる。
これが節点の移動先を決定する際の本質だ。
以上の考え方はゴムのように大きく変形するものも含めた一般的な考え方だ。
ただし多くの場合、材料力学では金属材料を相手にすることが多く、こういった極めて微小な変形を扱うような場合にはさらに踏み込んで考える必要がある。(“踏み込んで”というよりはむしろ、より問題を簡単に扱うための処理だ。)
つまり、『変形量がめちゃくちゃ小さい』ことを考慮すると、部材先端の動きを簡略化して考えることができる。
金属材料のように変形量が微小な場合は、先端の動きを超拡大してやらないといけない。
超拡大してみると、先端の移動先としてあり得る場所は、下図のように円弧状ではなく直線で表現できるようになる(青破線)。図のように部材はほとんど回転しないので、変形後の部材は元の部材と平行に描ける。
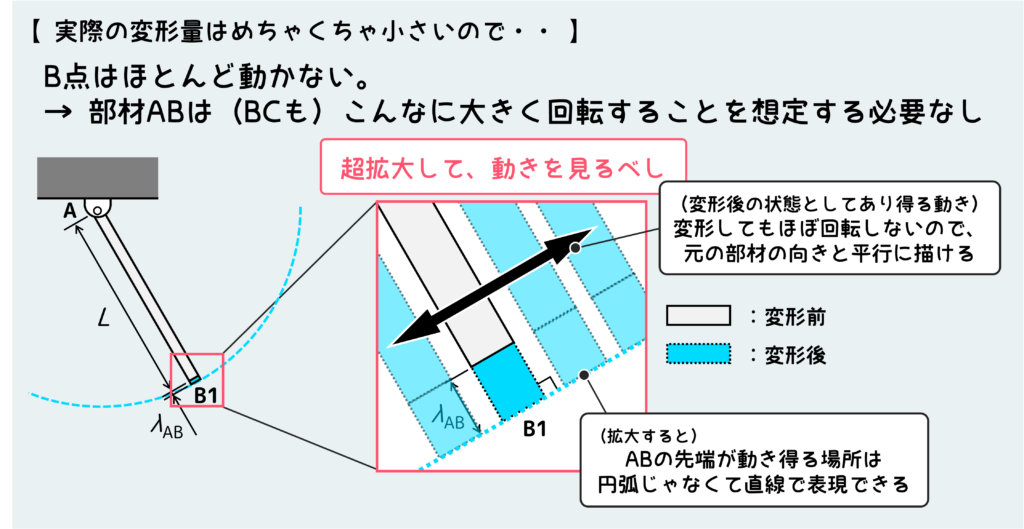
この考え方をもう1つの部材CBにも適用しないといけない。
なので、結局節点Bの移動先は下図のようにAB+λABの先端から引いた垂線(青破線)とBC+λBCの先端から引いた垂線(黄色破線)の交点に決まる。
このB’点がABおよびBCの変形を両方同時に満たす唯一の点である。
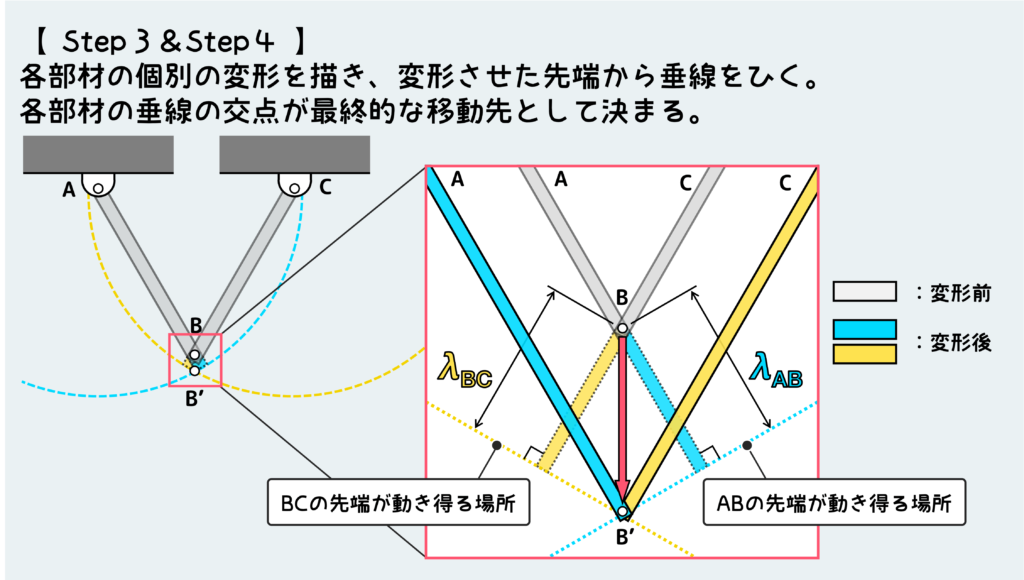
さて、ここまで出来ればあとは図から三角比をうまいこと使って、実際の移動距離を計算するだけだ。
ここでもやはり図を丁寧に描くことが極めて重要なことだ。図をきれいに描いてさえいれば、どの部分の角度がどのくらいになるか一目で分かり、どういう計算で変位を計算できるか一発で掴める。
すなわち、しょうもないミスを減らすことにつながる訳だ。
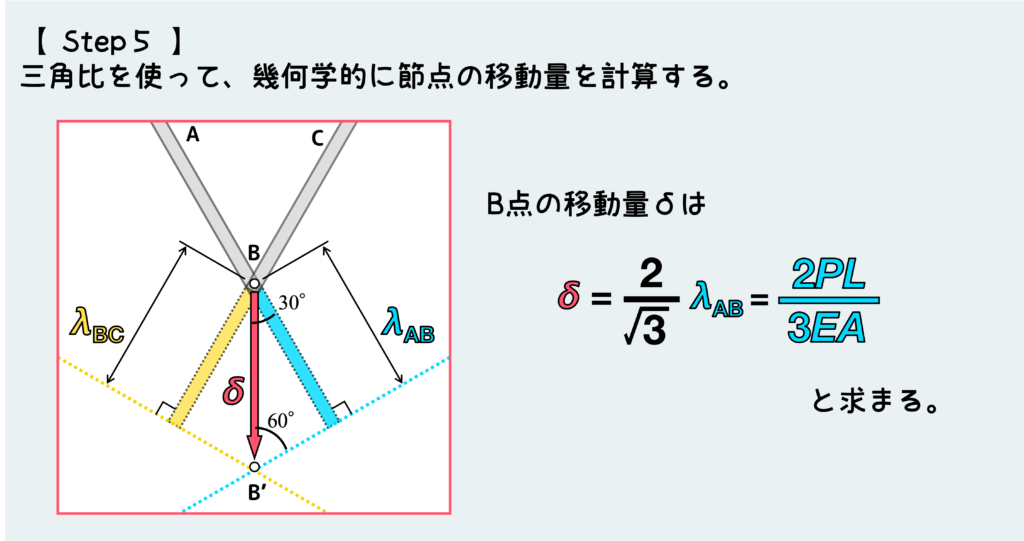
以上が、トラス上の節点の変位を求めるための基本的な流れだ。
あとはこの基本を踏まえて、場数を踏めばしっかり理解できるはずだ。
では次の例題を考えて、手順をしっかりマスターしよう。
まあさっきの問題と角度が少し違うだけなので、ほとんど同じ内容だ。この問題のB点の変位を求めてみよう。
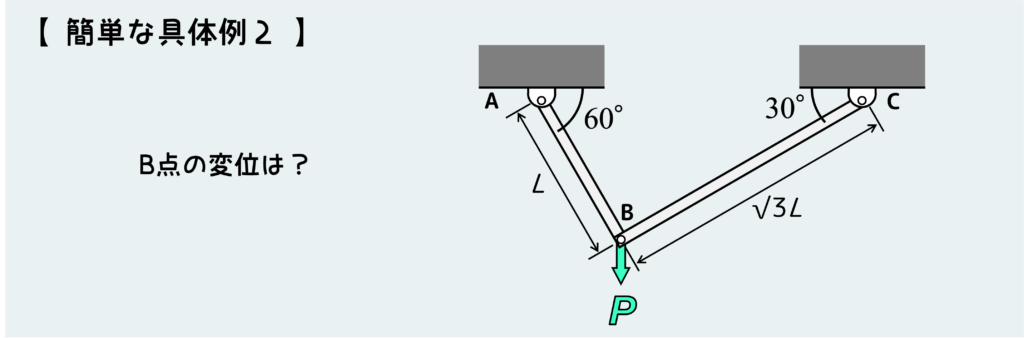
まず手順1として、各部材に働く力を求める。これには節点法を使う。
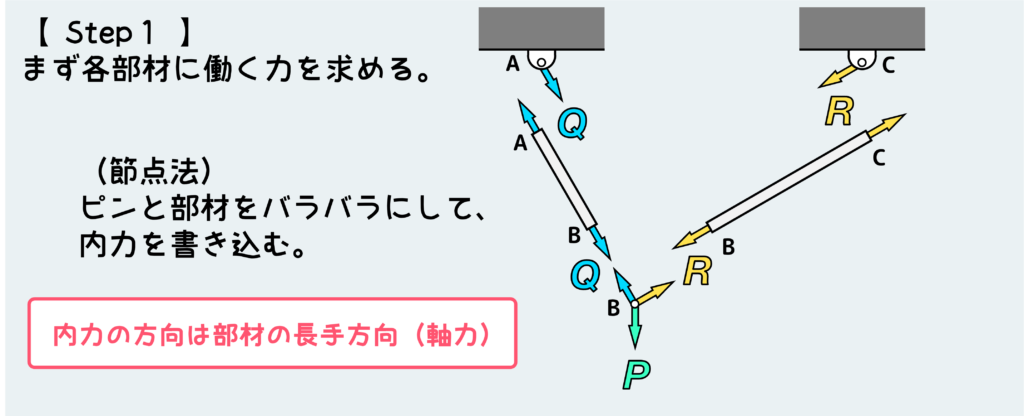
下図のように節点Bに働く力のつり合いを考える訳だが、ベクトル和の考え方を使えば簡単だ。
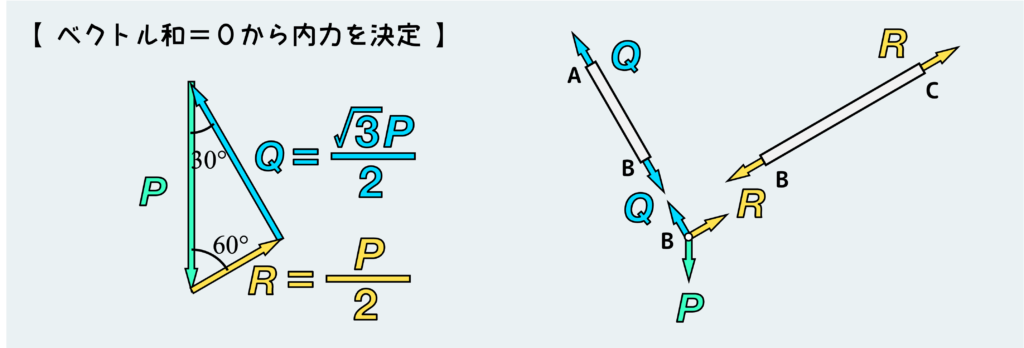
部材に働く力が求まったら、各部材の変形量を公式を使って計算しておく。
伸びなのか縮みなのか間違えないようにしよう。今回は両方とも引っ張りを受けているので伸びる。
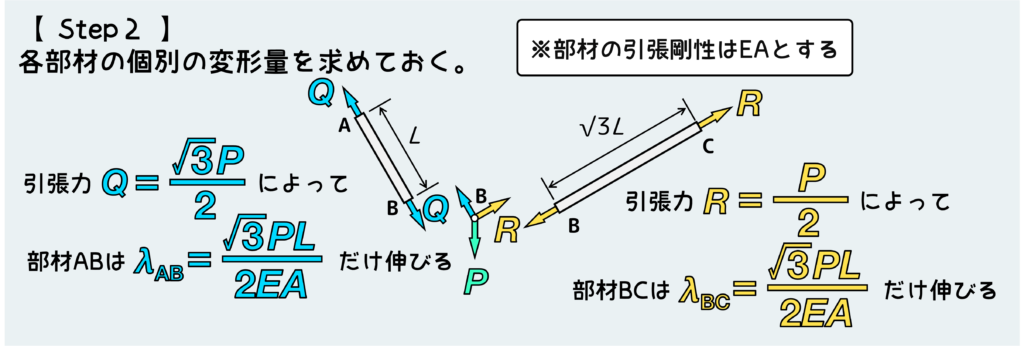
ここからがトラス変形の考え方の肝だ。
今考えている節点B付近の変形の様子を超拡大して図に描く。
下図のように、部材ABをλABだけ伸ばして、その先から垂線(青破線)を引く。さらに部材BCをλBCだけ伸ばして、その先から垂線(黄色破線)を引く。
この2本の破線がそれぞれの部材の先端が移動し得る場所なので、両方の部材の変形が同時に成り立つためには、節点Bがこの交点に移動しなくてはならない。
てことで、節点Bの移動先が決定できる。
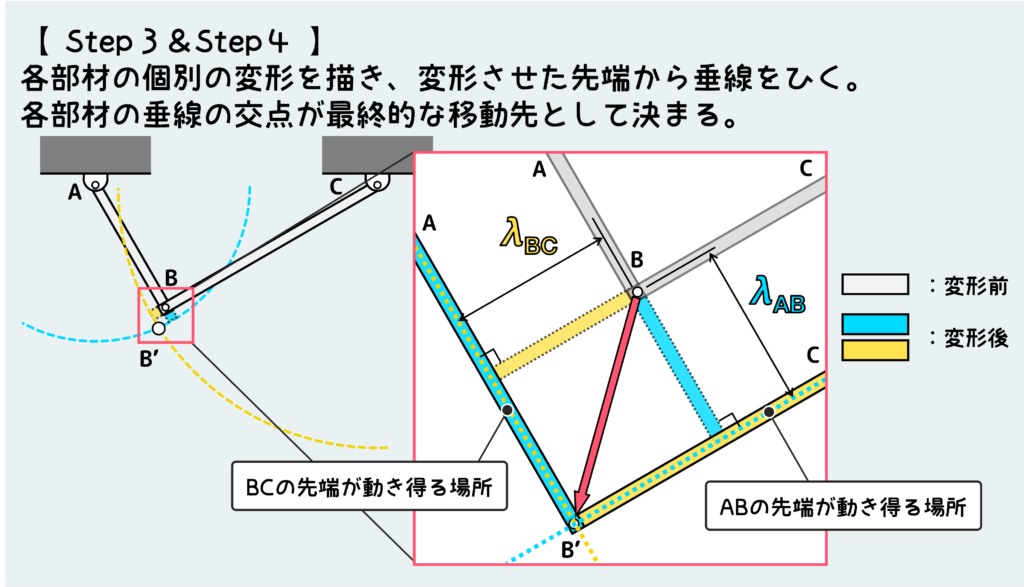
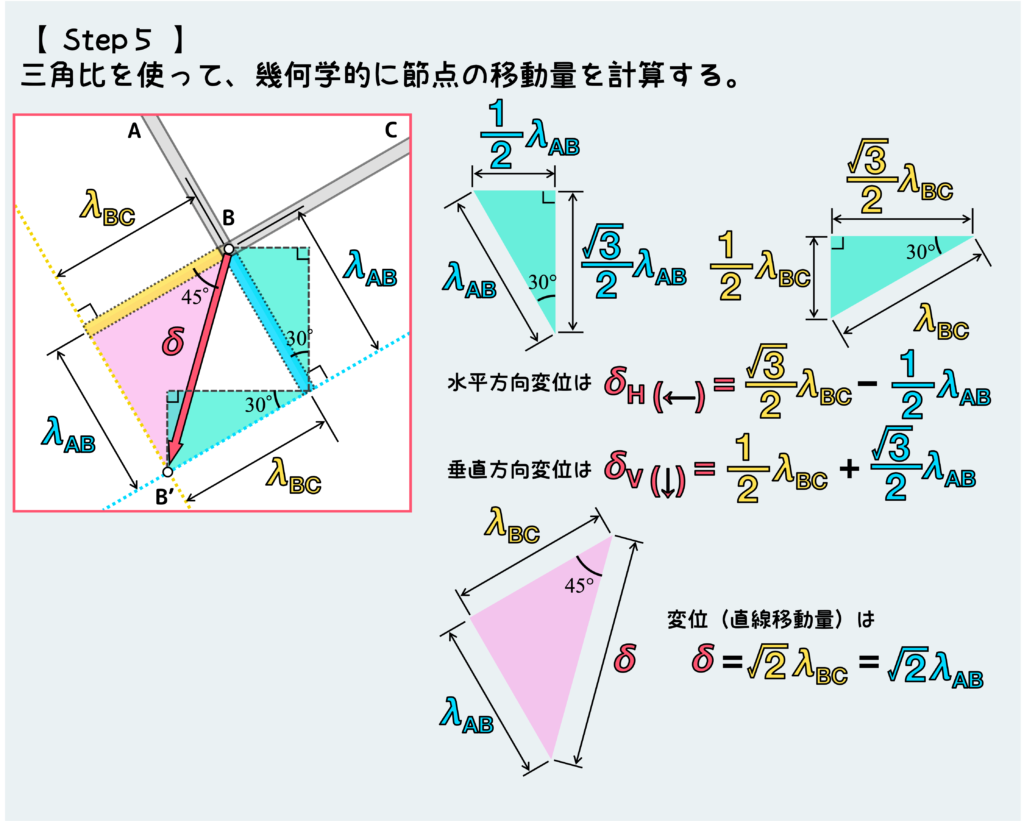
あとは図から三角比を使って変位を計算するだけだ。
今回は30度とか60度とか分かりやすい角度しか登場しないので、下のように簡単に求めることができる。
まとめ
トラスの変形を幾何学的に考えることについて、超詳しく説明してきたが理解できただろうか。
コツさえ掴めばそんなに難しくはないはずだ。
次以降の記事では、色んなバリエーションの問題や、トラスの不静定問題などについても説明していきたいのでぜひそちらも合わせて読んでもらいたい。
- トラスの変形を考える上で重要なのは、各部材が回転することの意味をしっかり理解すること。
- ある節点は、その節点につながっている部材すべての変形が同時に成り立つような点に移動する。
- Step 1:部材に働く力を求める。
- Step 2:各部材の個別の変形量を求める。
- Step 3:各部材の変形させた図を描き、その先端から部材に垂直な線を引く。
- Step 4:部材それぞれから垂線を引いたら、これらの交点が節点の移動先。
- Step 5:図から三角比などを利用して、節点の移動量を計算する。