角度の単位(rad)ラジアンってよく登場するんだけど、イマイチよく分かっていないという人は多いだろう。普通に人と話をするときには(°)で問題はない。しかし、公式の中や理論式の中では(rad)を使わないとならない。
今回は番外編として、角度の単位(rad)について簡単にまとめよう。
- 円周率は「円周の長さが直径の何倍か」を表したもの
- 角度の単位(rad)とは、半径 ”1” の扇型の円弧の長さを使って、先端の角度の大きさを表したもの
- 360(°)= 2\(\pi\)(rad)、180(°)= \(\pi\)(rad)
- 任意の角度★(°)= \(2\pi\times\large\frac{★}{360}\)
- 先端の角度の単位が(rad)のとき、(円弧の長さ)=(半径)×(角度)
夢へ駆ける少女の姿に感涙!!
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか?」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい!」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanならなんと3巻まで無料で読めてしまいます!まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです!
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!
まずは円周率 \(\pi\) について
ラジアンの話に入る前に円周率について少しだけ説明しよう。
円周率って当たり前みたいに使っているけど、そもそも何だろうか?平たく言うと、円の直径に対する円周の長さの比率を表したものだ。つまり、円周の長さは直径の何倍か?を表したものが文字通り「円周率」ってわけだ。

ある直径 d の円があるとすると、その円周の長さは\(\pi d\)となる。
(少し語弊があるかもしれないが)この円周の長さを利用して、半径”1”のときの(円弧の長さ)を角度の大きさを表現する物差しにしたのが(rad)ラジアンだ。
こういうものには「なんで?」とかそんな疑問は持ってはいけない。1(g)ってこのぐらいの重さなんですよーと言われて「なんでそれを1(g)にしたんだ!」って言っても仕方がないだろう。(実際には理由がないってことはないだろうけど、そこまで掘り下げる必要はないってことだ)
(rad)ラジアンとは?

もう一度言おう。半径”1”のときの(円弧の長さ)を角度の大きさを表現する物差しにしたのが(rad)ラジアンだ。言葉だと分かりにくいが、上の絵を見てもらうと少しはイメージできると思う。
どういうことか?具体的に図を見ながら考えた方がいいだろう。
まず、分かりやすく丸々一周分、つまり360(°)はどう表現できるだろうか?さっき説明した通り、半径1の円の360(°)分の円弧の長さ(つまり円周の長さ)は直径に円周率\(\pi\)をかければいいので、”2\(\pi\)”になる。これが360(°)に相当するということなので、360(°)= 2\(\pi\)(rad)ってことだ。

では次に円から一部を切り出した扇型を考えてみよう。例えば、下の絵のように円弧の長さが ”1” になるように扇型を切り出した場合、その先端の角度は定義から 1(rad)になる。さらに、もし円弧の長さが ”2” になるように切り出せば、先端の角度は 2(rad)だ。
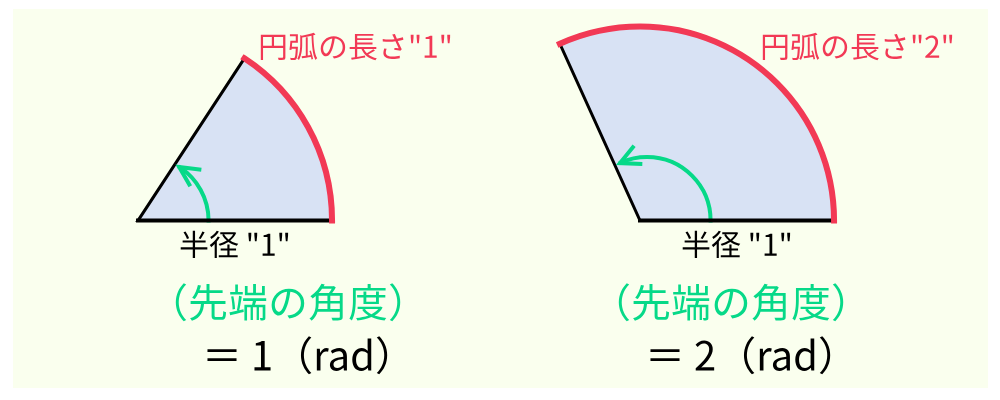
理解できただろうか?円弧の長さがそのまま角度の大きさを表しており、このときの単位を(rad)と呼ぶことにしたわけだ。
では、任意の角度を(rad)で表したいときはどうすれば良いか。例えば、先端の角度が★(°)の場合を考えてみよう。これも、要は半径 ”1” のときに円弧の長さがどれくらいになるかを考えればいいので、下の絵のように考えれば簡単だ。つまり、任意の角度★(°)は \(2\pi\times\large\frac{★}{360}\) というように表すことができる。★のところに自分が求めたい角度(°)を入れれば(rad)に変換される。

360(°)= 2\(\pi\)(rad)、180(°)= \(\pi\)(rad)
任意の角度★(°)= \(2\pi\times\large\frac{★}{360}\)
(rad)ラジアンの最も大事な性質
上で説明した(rad)ラジアンの定義をより一般的なケースに拡張してみよう。そうすると、最も重要な性質が見えてくる。
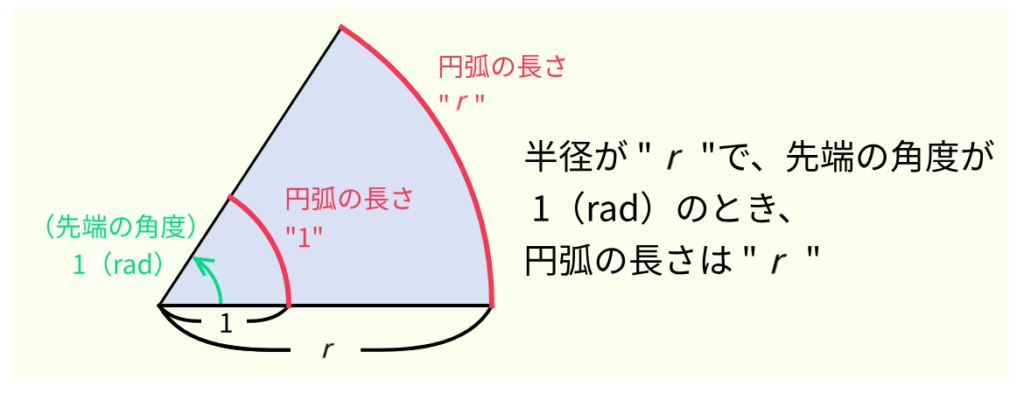
さっき見た半径 “1” で角度 1(rad)の扇型の上に、同じ角度で半径 ” r ” の扇型を考えてみよう。さっき説明した通り、半径 “1” の場合の円弧の長さは “1” だ。では、半径 ” r ” の場合はどうだろう?この2つの扇型は相似形なので、半径が r 倍になったということは、円弧の長さも r 倍されて、 ” r ” になる。
先端の角度が 2(rad)ときも同じように考えると、半径 ” r ” の場合の円弧の長さは ” 2r ” となることが分かるだろう。
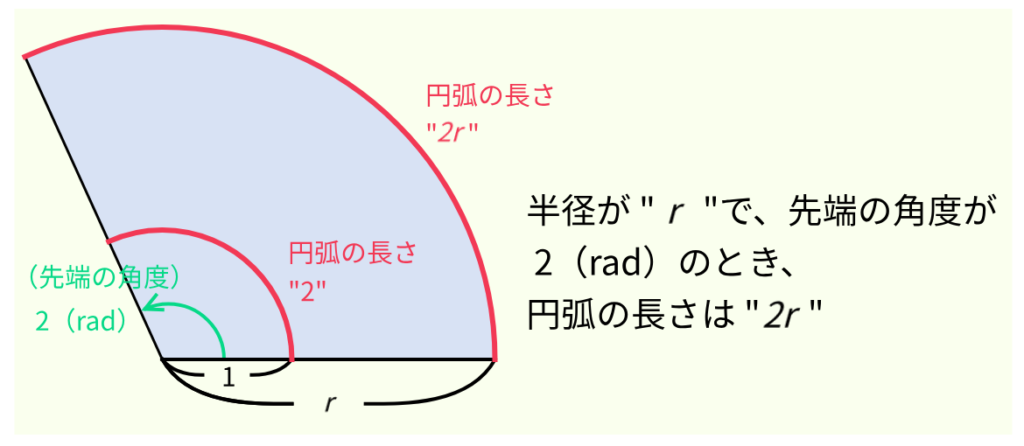
ここで何が言いたいかというと、ある角度 \(\theta\)(rad)を先端に持つ扇型の円弧の長さは、半径に \(\theta\)(rad)をかけたものになる、ということだ。

これは非常に重要な性質だ。材力だけでなく、物理系の学問でときどき「\(\theta\)が十分小さいという条件下で\(\sin\theta\)を\(\theta\)で近似する」みたいな近似が出てくるが、これは角度(rad)の性質を利用したものだ。材力でも頻繁に登場する。
なんでこんな近似ができるか、については次の記事で解説したい。
 「sinθをθで近似する」ってどうしてそうなるのか詳しく説明します。【番外2】
「sinθをθで近似する」ってどうしてそうなるのか詳しく説明します。【番外2】
とにかくここでのポイントは次の通り。
- 円周率は「円周の長さが直径の何倍か」を表したもの
- 角度の単位(rad)とは、半径 ”1” の扇型の円弧の長さを使って、先端の角度の大きさを表したもの
- 360(°)= 2\(\pi\)(rad)、180(°)= \(\pi\)(rad)
- 任意の角度★(°)= \(2\pi\times\large\frac{★}{360}\)
- 先端の角度の単位が(rad)のとき、(円弧の長さ)=(半径)×(角度)
理工系人材必読の超おもしろ漫画!!
連載中
『まずは音を出して 音を出さなきゃ音楽は始まらないのよ』
今、忘れかけていた夢への一歩を踏み出す!
いつの間にか多くの人は昔描いた夢のことを忘れてしまう。『宇宙兄弟』は“夢を追うのに遅すぎるなんてことはない”ということを教えてくれます。キャリアや進路に悩むすべての人の背中を押してくれる言葉にあふれている『宇宙兄弟』は多くの社会人や大学生から大絶賛されています。
宇宙開発や飛行士の活動をリアルに描く本作は、理工系の人の知的好奇心を刺激し、未知の問題へ向き合う姿勢を学べる必読書と言っても決して過言ではありません!
ebookjapanなら3巻まで無料で読めるので、気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!





