前回の『応力』に関する記事に続き、今回の記事では『ひずみ』についてだ。ひずみももちろん材料力学においてとっても大事な要素だ。基本的なことではあるけど、だからこそ今回の記事を読んでしっかり理解してほしい。
応力についての解説記事はこちらをどうぞ↓
 材料力学 応力とは?10分で完全に理解できる 基本かつ超重要な解説【材力 Vol. 2-1】
材料力学 応力とは?10分で完全に理解できる 基本かつ超重要な解説【材力 Vol. 2-1】
- ひずみとは、変形量の大きさを表すパラメータであり、絶対量でなく変化の割合を表している。
- ひずみには、『垂直ひずみ』と『せん断ひずみ』の2種類がある。
- ひずみには原則単位は付かないが、せん断ひずみは角度の変化を表すので(rad)を付けることもある。
- 材料力学で取り扱うひずみの大きさは、基本的にめちゃくちゃ小さい。
- 材料力学で扱うような変形(弾性変形)では、応力とひずみの間にはフックの法則が成り立つ。
夢へ駆ける少女の姿に感涙!!
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか?」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい!」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanならなんと3巻まで無料で読めてしまいます!まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです!
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!
ひずみって何? ー変形量の大きさを表すパラメータですー
『ひずみ』っていう言葉も『応力』とおなじく、大学で材料力学を学ぶときに初めて聞く言葉ではないだろうか。ひずみに関しては応力ほど難しいものではないと思うが、この記事で一応重要なところを触れておこう。
まず、ひずみとは何か?
これはずばり変形量の大きさを表すパラメータなんだが、大事なことは変化の割合を表しているということだ。つまり逆の言い方をすると、変形量の絶対値ではないということを理解しておくべきだろう。
下の図を見てみよう。長い棒と短い棒があり、どちらも伸びている。図の通り、変形量の絶対値(伸び)は長い棒の方が短い棒よりも大きい。しかし、ひずみ(つまり変化の割合)で言うと短い棒の方が大きい。
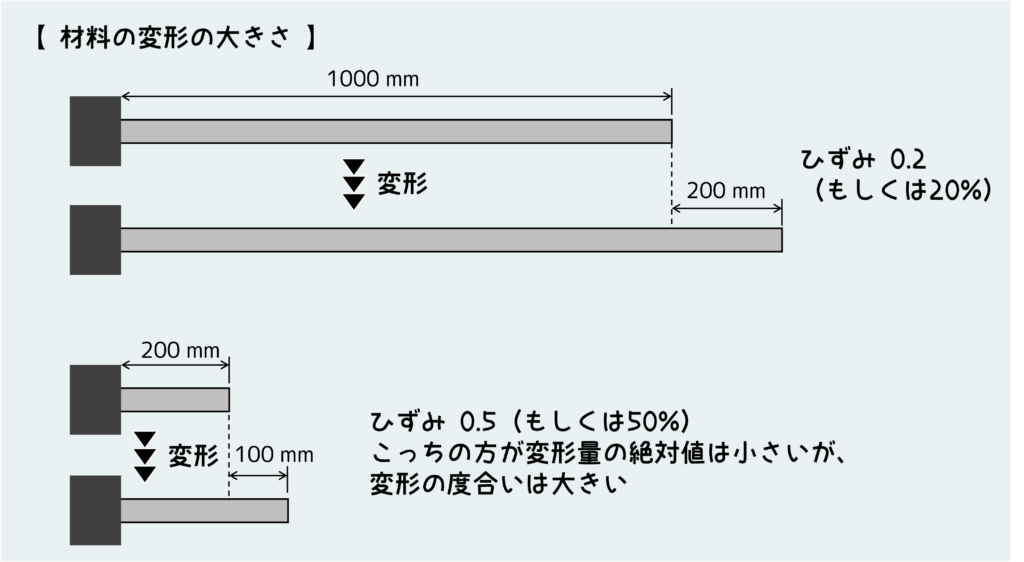
仮にこの材質のポテンシャル的に伸びれる限界(破断伸び)が60%だとしたら、当然短い棒の方が破壊に近い状況である。絶対値だけを見ていてはこういう評価はできない。このように、材料の変形度合いの大小を議論する場合は、絶対値ではなくひずみで議論する方が適切だ。
もちろん、絶対値としての変形量が重要になる場面もあるとは思うが、要は使い分けが大事だってことだ。
ひずみについて理解しておくべき事4つ
いくつかひずみについて理解しておくべきことを説明していこう。
まず種類についてだ。応力に種類があったように、ひずみもいくつかの種類に分けられる。基本的にひずみの種類は応力の種類に対応している。
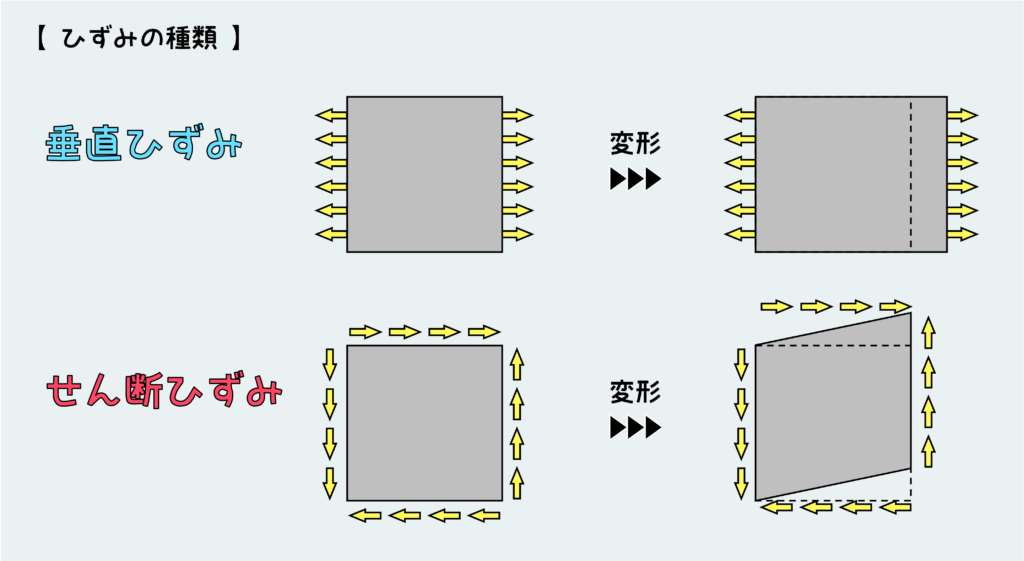
つまり、垂直応力によって生じる(その応力の方向の)ひずみは『垂直ひずみ』であり、せん断応力によって生じる(その応力の方向の)ひずみは『せん断ひずみ』である。
垂直ひずみは、例えば真四角の形状のものが真四角を保ったまま伸びたり縮んだりするような変形である。一方、せん断ひずみは真四角の形状がゆがんで形状が変わるような変形のことである。言葉で説明するより図を見た方が理解しやすいだろうから、下の図を見て違いをはっきりと理解してほしい。
ちなみに、垂直ひずみは “ε “(イプシロン)で表し、せん断ひずみは “γ “(ガンマ) で表す。
場合によっては『曲げひずみ』っていう言葉を使う人もいるかもしれない。これは当然曲げ応力によって生じるようなひずみ分布のことを言うのだが、ある一箇所に注目するとそこで起きている変形は結局のところ垂直ひずみであり、厳密にひずみの種類としてカウントする必要はないだろう。
つまり、ひずみの種類としては『垂直ひずみ』『せん断ひずみ』の2種類あると認識しておけば良い。
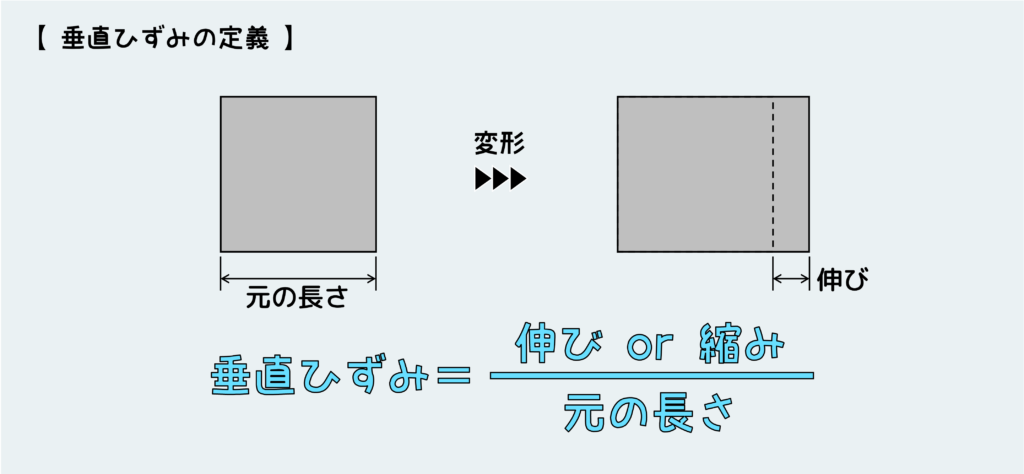
さて、ではどういう風にひずみを表現するかという話に移ろう。ひずみの定義は、その材料が単位長さ当たりにどれだけ変化したかを表すものなので、変形量を元の長さで割ることで得られる。
単位について
変形量(長さ)を長さで割ったものなので、ひずみに単位はない。なので、ひずみは0.001とか0.0001とかって表現する。だけど、実際言ったり書いたりするときに使いにくいよね。なので、実際には「%」とか「με(マイクロストレイン)」を使うことが多い。
「%」については説明不要だと思う。ひずみ0.1のときに10%と言ったりする訳だ。比較的大きな変形量を相手にするときに使うことが多い。
「με(マイクロストレイン)」については初めて聞く人ばかりだろう。これは厳密には単位ではなく、便宜上使いやすいように作り出した擬似単位だ。μが10-6という意味なので、1μεはひずみ0.000001(1×10-6)を表す。正式な表現ではないが、現場では使うことも多い。
ただ、せん断ひずみについては、下記の通り結果として角度を表すことになるので、(rad)を付けて角度として表現する場合が多い。
垂直ひずみ
垂直ひずみは、材料が垂直応力によって伸びたり、縮んだりするときの変形量を示している。
垂直ひずみε の定義は下図の通り。
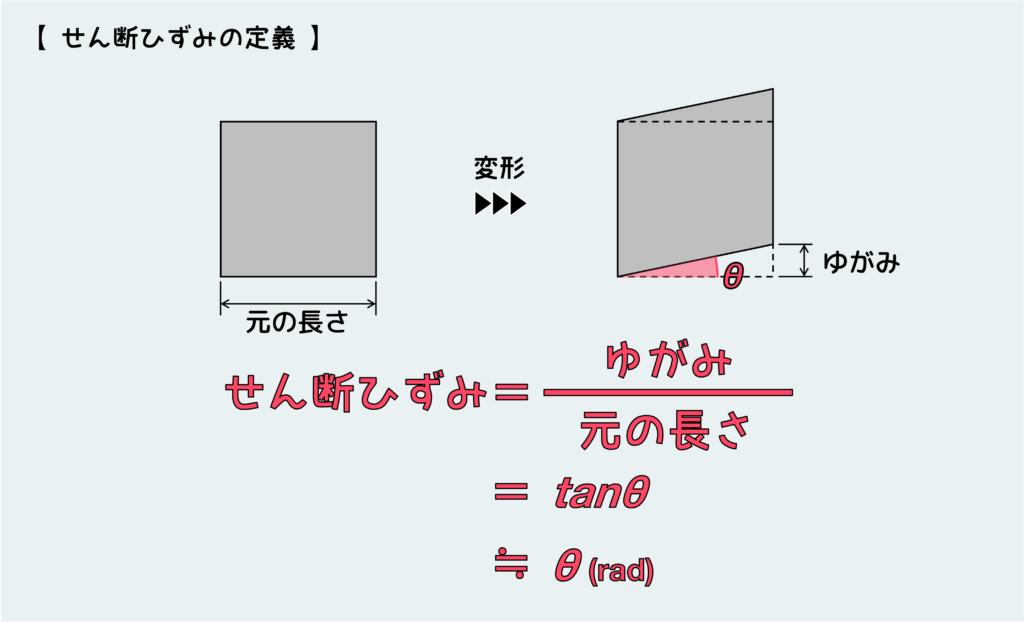
せん断ひずみ
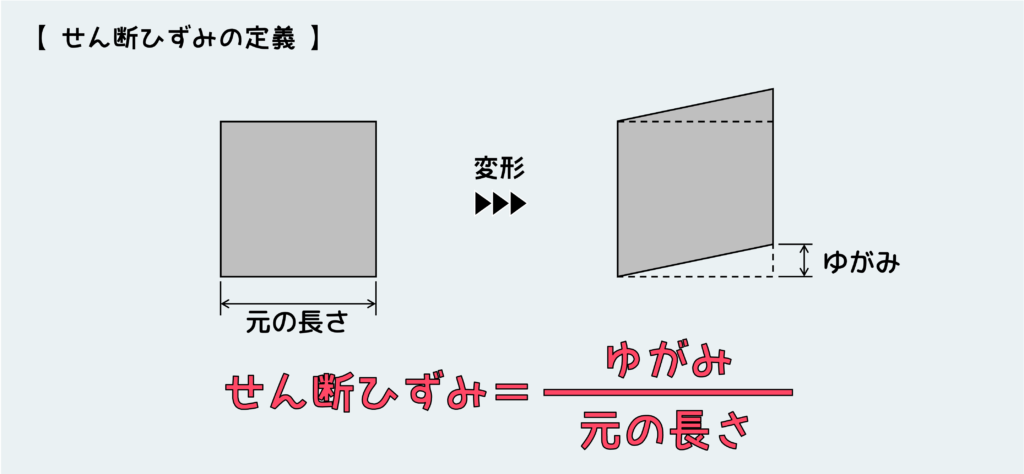
せん断ひずみは、せん断応力によって形状のゆがみが生じるときの変形量を示している。
せん断ひずみγ の定義は下図の通り。
定義としては上のように表せるんだけど、材料力学で扱う変形量はものすごく小さいので、よく出てくる角度に関する近似を利用できる。よく出てくる角度に関する近似とは以下のようなものだ。
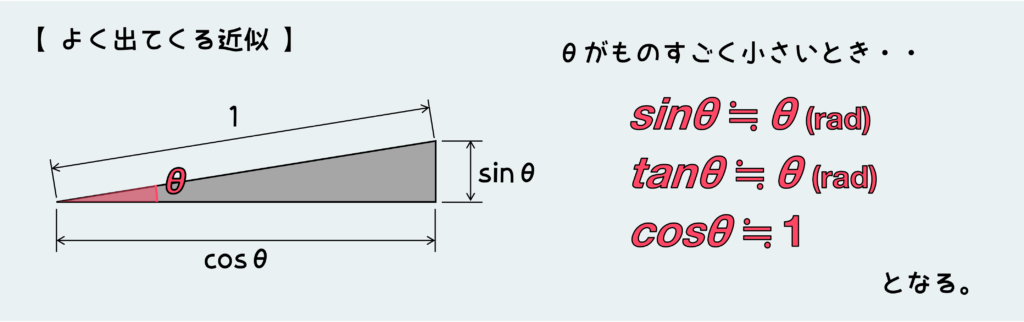
この角度に関する近似を利用すると・・
となり、結局せん断ひずみγ は角度変化そのものを表すことになる。このとき重要なのは、この角度変化の単位は(°)ではなく(rad)であるということだ。
この辺の角度近似に関することを疑問に感じる人は、以下の記事にわかりやすくまとめているので、ぜひ読んでみてほしい。
 「sinθをθで近似する」ってどうしてそうなるのか詳しく説明します。【番外2】
「sinθをθで近似する」ってどうしてそうなるのか詳しく説明します。【番外2】
後でも少し触れるが、材料の変形には『弾性変形』と『塑性変形』があり、基本的に材料力学で扱うのは変形量の小さい『弾性変形』の範囲だ。
材料に負荷をかけていくと、しばらくはフックの法則(後でまた出てきます)に従って負荷の大きさに比例して変形していく領域があり、これが弾性変形範囲である。弾性変形はかけている負荷を取り除くと変形前の状態に戻ることが特徴だ。そして、あるところまで負荷をかけると、弾性変形の限界が来て塑性変形に切り替わるようなポイントがやってくる。これを『降伏』という。
材料力学で取扱うのはこの降伏が起きる前、つまり弾性変形の範囲である。もちろん材料によって違うが、主な金属材料において、降伏が起きるのはひずみがおよそ0.002程度のときである。なので、材力で登場するひずみはだいたい10-4(0.0001)〜10-3(0.001)のオーダーだと考えて良いと思う。
これは実際どのくらいの変化かと言うと、そりゃーもうめちゃくちゃ小さいのである。もう目に見えないレベルの変化だと思って良い。例えば長さ50cmの棒が一様に伸びたとして、そのときのひずみが0.001だとしたら長さの変化(伸び)は0.5mmである。いかに小さい変形か分かるだろう。
一方、塑性変形というのは降伏後の大きな変形のことで、負荷を取り除いても変形は元に戻らない。金属がぐにゃっと曲がったりしているのを見た事あるかもしれないが、あれは塑性変形な訳だ。
塑性変形の範囲は(少なくとも学部生の間は)材料力学では扱わず、塑性力学というまた少し違う学問の範囲になる。
材料が変形する様子を想像すると分かるが、材料にかかる負荷の大きさと変形量の大きさにはある関係性がある。別に材料力学を勉強していない人だって普段の生活の中で、負荷が大きくなればなるほど材料は大きく変形することを実感できると思う。
材料力学の中では、これを『フックの法則』と呼ぶ。フックの法則とは、応力とひずみが比例関係を持つことであり、「σ =Eε 」という関係式で表される。E というのはこの比例関係の程度を表す比例定数であり、ヤング率もしくは縦弾性係数と呼ばれるものだ。ヤング率E は材料の変形しにくさを表すもので、材質によって決まる材質パラメータであることをよく理解しておこう。
材料、とくに機械工学で主に取り扱う金属材料の変形には「弾性変形」と「塑性変形」がある。フックの法則が成り立つのは「弾性変形」範囲のみであり、弾性範囲を超えて塑性変形をしている材料にはもはやフックの法則が成り立たないことに注意しよう。
また、せん断応力とせん断ひずみについても同様にフックの法則が成り立ち、この時の比例定数はG(横弾性係数)である。つまり、「τ =Gγ 」である。
この辺りのことを含めて、応力とひずみの関係については下の記事で詳しく解説するので、気になる人はぜひそっちも読んでみてほしい。
 材料力学 フックの法則が使える時と使えない時の違いちゃんと分かってる?【Vol. 2-3】
材料力学 フックの法則が使える時と使えない時の違いちゃんと分かってる?【Vol. 2-3】
まとめ
ひずみも応力と同じく、材料力学において超基本的な物理量である。
この記事で紹介したような重要ポイントをよく理解して、応力もひずみも使いこなしてほしい。
次の記事では、応力とひずみの間にある関係について詳しく説明したいと思うので、ぜひ読んでみてほしい。
- ひずみとは、変形量の大きさを表すパラメータであり、絶対量でなく変化の割合を表している。
- ひずみには、『垂直ひずみ』と『せん断ひずみ』の2種類がある。
- ひずみには原則単位は付かないが、せん断ひずみは角度の変化を表すので(rad)を付けることもある。
- 材料力学で取り扱うひずみの大きさは、基本的にめちゃくちゃ小さい。
- 材料力学で扱うような変形(弾性変形)では、応力とひずみの間にはフックの法則が成り立つ。
研究者を志す者 必読!!
全8巻完結
こんなにも知的探究心を刺激される漫画があったとは!
真理のために命をかけた先人たちの物語。
この作品は、現役研究者である私・ぽるこが衝撃を受けた作品として、特に研究者およびこれを志す者には強く本気でオススメします。今ある常識を疑う心、誰に何を言われようと真理を追求する姿勢に触れ、心が動くこと間違いありません。
私自身、世界のトップ研究者だった師匠によく言われた言葉を思い出します。“目の前の現象に楽な答えを持ち出し、疑うことをやめ、真理の追求という困難な道から逃げていないか!?”
本作はこういった研究者の気概なるものを感じる、必読の価値ある一冊です。全8巻ですでに完結していますし比較的手軽に一気読みできます。気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!




