さて今回の記事では、トラスの問題について徹底的に解説したい。
トラス構造は鉄橋やいろんな構造物で実際に利用されているものなので、非常に重要だ。しかし、学生のみなさんの中には苦手な人も多いと思う。
個人的にはトラスの変形の考え方が難しいのではないかと思う。でも実はコツさえ掴めば何も難しくない。教科書では説明されていないポイントを徹底的にわかりやすく解説したいと思うので、ぜひ一連のトラスの記事を読んでみてほしい。
今回はまず、節点法による力の伝わり方の考え方について解説していく。
切断法については次の記事を読んでほしい。
材料力学 10分で絶対分かるようになるトラス問題（切断法による力の伝わり方編）【Vol. 3-5】
また、変形量の考え方は以下の記事にまとめている。これを読めば絶対分かるようになると思うので、トラスの変形に苦しんでいる人は絶対読んで欲しい。
材料力学 10分で絶対分かるようになるトラス問題（変形量編）【Vol. 3-6】
- トラス部材には軸力しか働かない。これのおかげで強い構造体にできる。
- 各部材に働く内力を明らかにするには節点法と切断法がある。
- 節点法はすべての部材に働く力を明らかにしていき、ある点の変位を知りたい場合に使える。あまりにも複雑なトラスの場合は不向き。
- 切断法は、複雑なトラスの中のある特定の部材に働く内力を知るのに向いている。
- どちらの方法も『切断した自由体の平衡条件を考える』のがポイント！
Contents
トラスとは
トラスとは下の絵のような構造体で、ポイントはすべての部材がピン接続されていることだ。
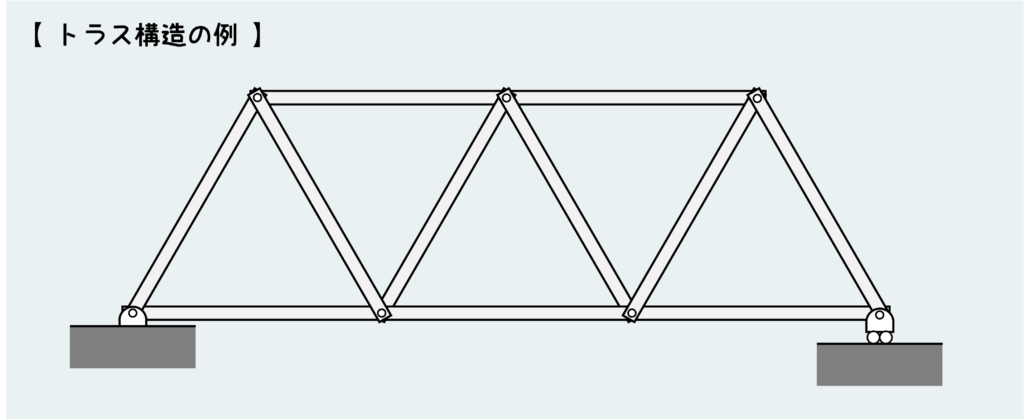
ピン接続というのは『部材同士が離れないように拘束している一方で、部材同士の回転は拘束しない』という特徴がある。これはつまりどういうことか言うと、『力を内力として伝えることができるが、モーメントは伝えられない』ということである。
これがピン接続の大きなポイントだ。
その結果、トラスを構成する部材には軸力（長手方向の力）しか働かないというめちゃくちゃ重要ポイントが生まれる訳だ。
少し詳しく説明しよう。
下の図のように、トラスからある部分の部材を切り出して考えてみる。
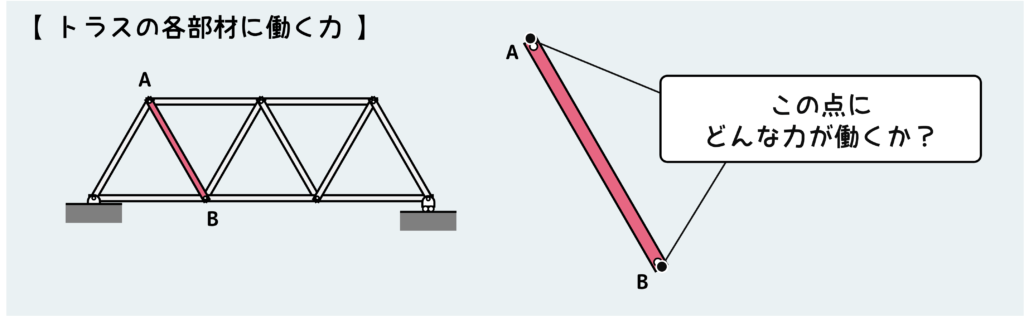
この部材の両端にはピンから内力が伝わってくるはずだが、さっき言った通り、ピンはモーメントを伝えることができないので、この部材の両端に書き込むことができる（つまり発生する可能性がある）内力は軸力とそれに垂直な方向の力だけだ。モーメントは書き込めない。
さあここでこの部材の平衡条件を考えてみよう。まず力の平衡条件が成り立つためには、両端にかかる軸力と垂直方向の力はそれぞれ同じ大きさで反対向きである必要がある。これで力は釣り合った状態になる。
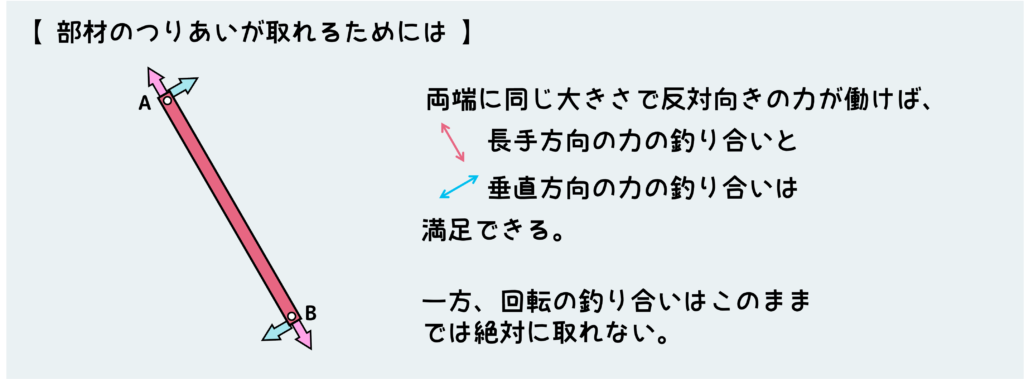
しかし、このままでは回転のつり合いが絶対に取れないことに気づくだろうか。軸力は回転に寄与しないのでこのままで大丈夫だが、垂直方向の力がどうしても回転の釣り合いをくずしてしまう。
力の釣り合いと回転の釣り合いを同時に満たすためにはどうしたらいいだろうか？答えは一つだ。
そう、垂直方向の力が”０”、つまり存在しなければいい。これ以外にこの部材の平衡条件が成り立つ術はない。
という訳で、トラスを構成する部材は必ず軸力のみを受ける状態になる。このことがトラス問題を考える上でめちゃくちゃ重要な前提となる。
絶対に軸力しか働かない！
一つ注意してほしいのは、これはトラスがピンで接続された構造体だから持つ特徴ということだ。これがピン接続ではなく剛接続で構成されるようなラーメン構造だと全く違う考え方が必要だ。
ラーメン構造については、またいつか説明したい。
軸力しか働かないおかげで、トラス構造は強いと言える。構成するひとつひとつの部材は細くても、全体として強い荷重を支えられる。
これはどういうことか？このことを理解するために、次のようなことを想像してみよう。
なんでもいいけど細い枝みたいなものを指の力で壊すことを考えてほしい。枝を引っ張って壊すことは相当なキン肉マンでない限りできない芸当だろう。だいたいの人は曲げて折ることで壊そうとするだろう。
指がかけることができる力（外力の大きさ）は変わらないはずだが、負荷形態（引張か曲げか）によって材料が受ける負荷（応力）は大きく変わってしまう。
つまり、『曲げ』というのは外力が小さくてもとても大きな応力を生み出すことができる負荷形態であり、材料にとってはなるべく避けたい状態である。
トラス構造は、ピン接続することで軸力しか働かない（曲げを受けない）状態にすることで壊れにくい構造になってる訳だ。
トラス構造は軸力しか働かないため強い！
例えば下図のように、長さ2Lの橋的なものでどんな応力が発生するか考えてみる。
左のものはトラス構造、右のものはただ長さ2Lの棒を渡しただけのものだ。左のトラス構造では、最大で引張力Pが働き、これによる引張応力は\(\displaystyle\frac{4P}{\pi d^2}\)である。一方右の構造では曲げが働き、これによる最大の引張応力は\(\displaystyle\frac{16PL}{\pi d^3}\)である。
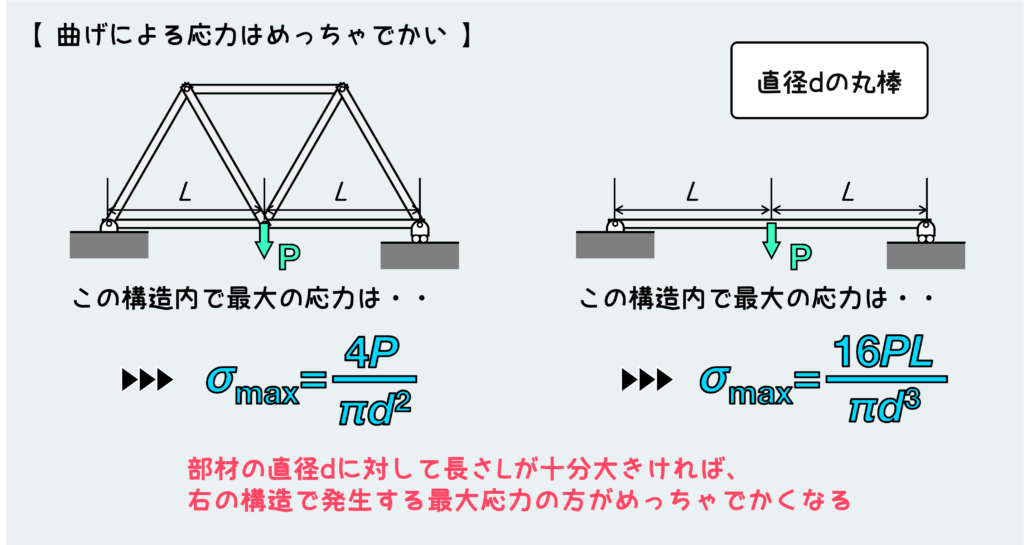
この部材の直径dに対して長さLが十分大きければ、右の構造に発生する曲げによる応力の方がトラス構造で発生する応力よりもとっても大きくなる。
このように、材料は多くの場合に曲げを受けるととたんに弱くなる。なのでなるべく曲げが発生しないような構造にすることは重要なことで、トラス構造にするのはその一つの手段な訳だ。
力の伝わり方（内力）を把握する
トラス構造において各部材に伝わる内力の大きさを把握する方法は２種類ある。
それが”節点法”と”切断法”だ。それぞれに以下のような特徴がある。
- すべての部材に伝わる力を明らかにできる。
- トラスのある点の変位を考えたいときには便利。
- トラスが複雑すぎると、平衡条件を考える数が膨大になり大変。
- トラス内のある特定の部材に働く力を知りたいときに便利。
- トラスがどんだけ複雑でも関係ない。
- 全部の部材の力や変形量を知りたいときには不向き。
上の特徴を踏まえて、使い分け方としてはこんな感じだ。
- トラスの中の特定のある部材に働く力を問われている時は”切断法”
- トラスを構成する三角形の数が２、３個の時は”節点法”で、４個以上の時は”切断法”
- すべての部材に働く力が知りたいときや、変形量を問われる場合は”節点法”
おおよそ上のような感じで使い分ければ良いと思うが、どちらの方法もちゃんと使えることが重要だ。
この後、やり方を丁寧に解説するので、しっかり身につけよう。
節点法のやり方と簡単な具体例
まず節点法のやり方だ。以下の手順に従ってやればOKだ。
まず何も考えずにすべてのピンと部材をバラバラにしていく。ここで切り分けたものはすべて自由体だ。これらの自由体は当然つりあいが取れていないといけない。
バラバラにしたピンの平衡条件から部材に働く内力を決定していく。外力が作用しているピンしかとっかかりがないので、これの平衡条件をまず最初に考える。平衡条件を考えるときのコツは『部材には軸力しか働かないこと』と『ベクトル和の考え方を使うこと』だ。
最初のピンの平衡条件を考えたら、それを元に隣り合う部材・ピンへと作用・反作用の法則を使って内力を伝えていく。さらにそこから、別のピンの平衡条件を考えて全ての部材に伝わる内力を決定していく。ポイントは『支点に接続されているピンに働く支点からの反力は支持方法によって変化する』ということ。
手順はこれだけだ。素直にこの手順を守れば何も難しくないので、苦手な人は素直にこの手順通りに解いてみてほしい。
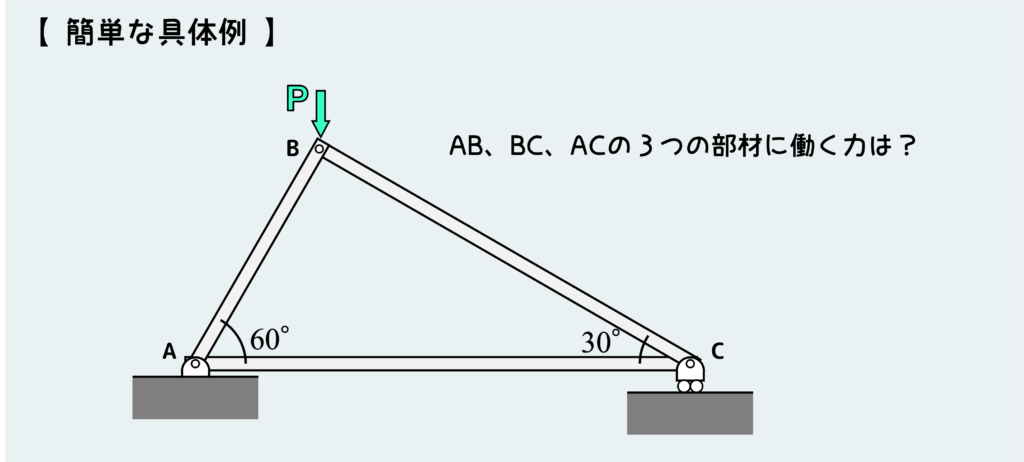
では簡単な具体例を通して、節点法のやり方を理解しよう。
下図のような問題を考えてみよう。
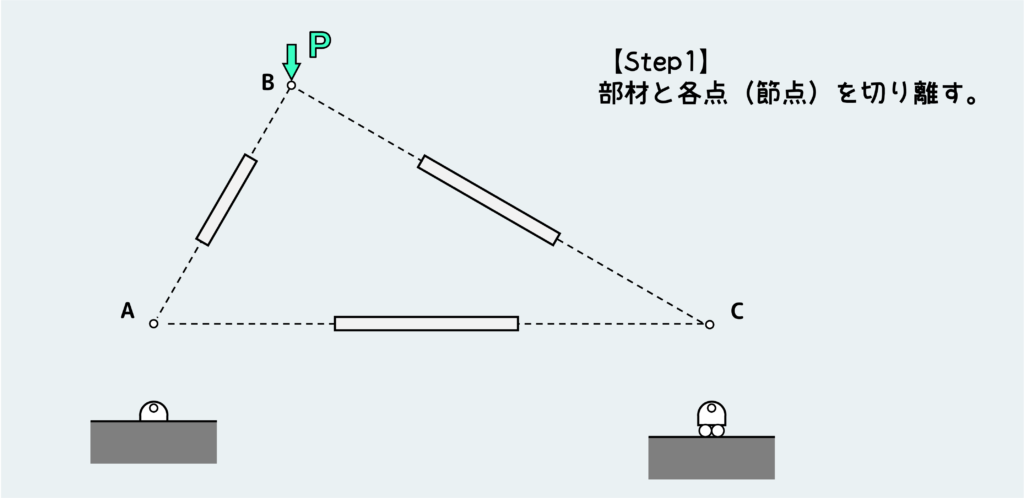
【Step １】まずは何も考えずにピン（節点）と各部材をバラバラに切り離す。
これらひとつひとつが自由体であり、それぞれ平衡条件を満たす必要がある。
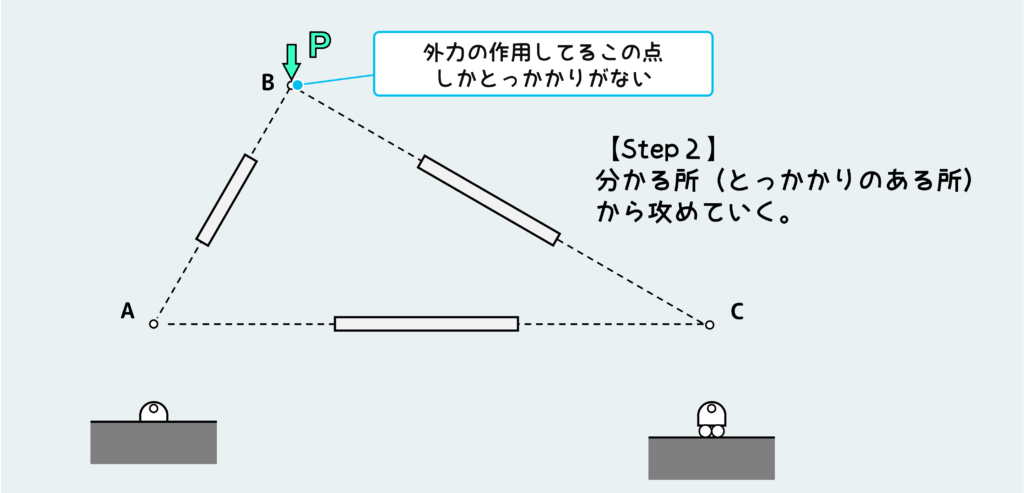
【Step ２】次に、これらの平衡条件を考えていく訳だが、どこからでも攻めていける訳ではない。
なぜなら、とっかかり（分かっている力）がないと考えるための足掛かりがないので何も進まない。なので、通常は外力が作用しているピンの平衡条件から考えていくことになる。
今回の場合は、下図のように外力Pが作用しているピンBの平衡条件を初めに考える。
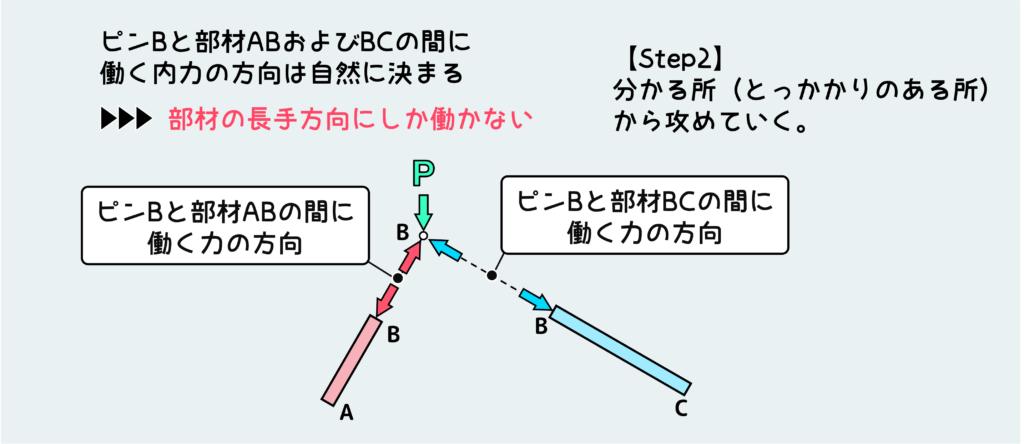
さて、ピンBの平衡条件をこれから考えるが、ここで思い出してほしい大事なことは『トラス部材には軸力（長手方向）の力しか働かない』ということだ。
ピンBに働く内力は、これに元々繋がっていた部材から受ける力になるので、部材ABから受ける力と部材BCから受ける力の２種類だ。で、これらの部材には軸力しか働かないので、ピンBが部材から受ける力の方向も、その軸力の方向になる（作用・反作用の法則）。
したがって、ピンBに働く内力２種の方向は下図のように自ずと決まってしまう。厳密に言うとこの時点では、内力の矢印の方向には引張・圧縮の２つの可能性が残されている。
これが分かれば、あとは平衡条件が成り立つように、この内力の大きさを決定すればよい。
さて、ピンの平衡条件を考える前に『ベクトル和』という考え方について触れたい。
材力で扱っている力もベクトルの１種なので、力を足し算するということはベクトルを足し合わせていくことになる。
『ベクトルの和』というのは、下の絵のように足し合わせたいベクトルを繋ぎ合わせていき、最初のベクトルのスタート地点から最後のベクトルのゴール地点を結んだもの（下図の黄色矢印）となる。ちなみに繋ぎ合わせる順番は関係ない。
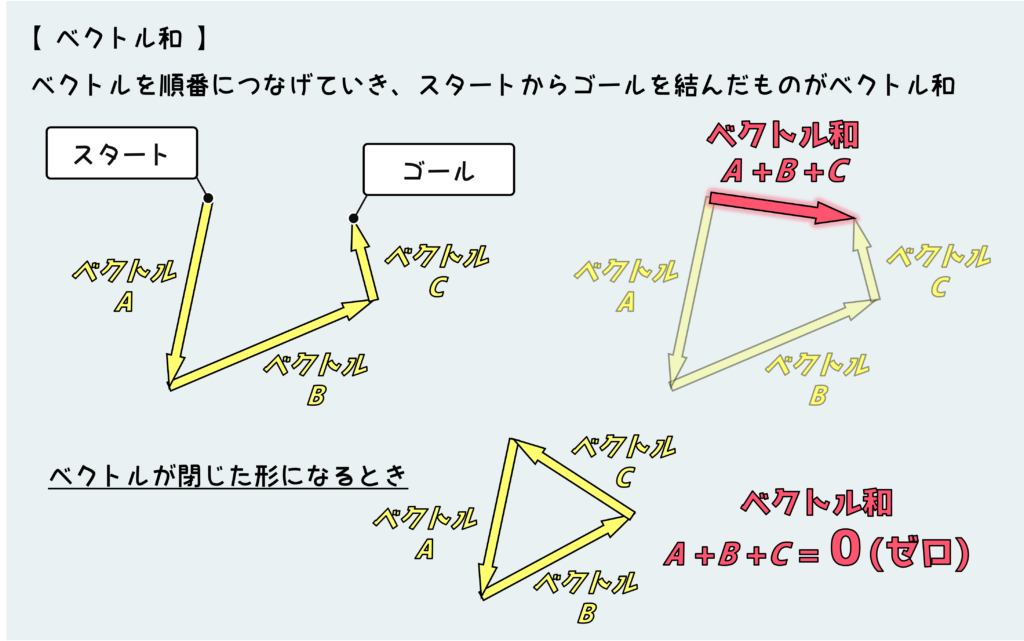
さて、ピンの平衡条件が成り立つということは、力の合計が“０”（ゼロ）になるということである。（ピンは点なので、回転の釣り合いを考える必要がない）
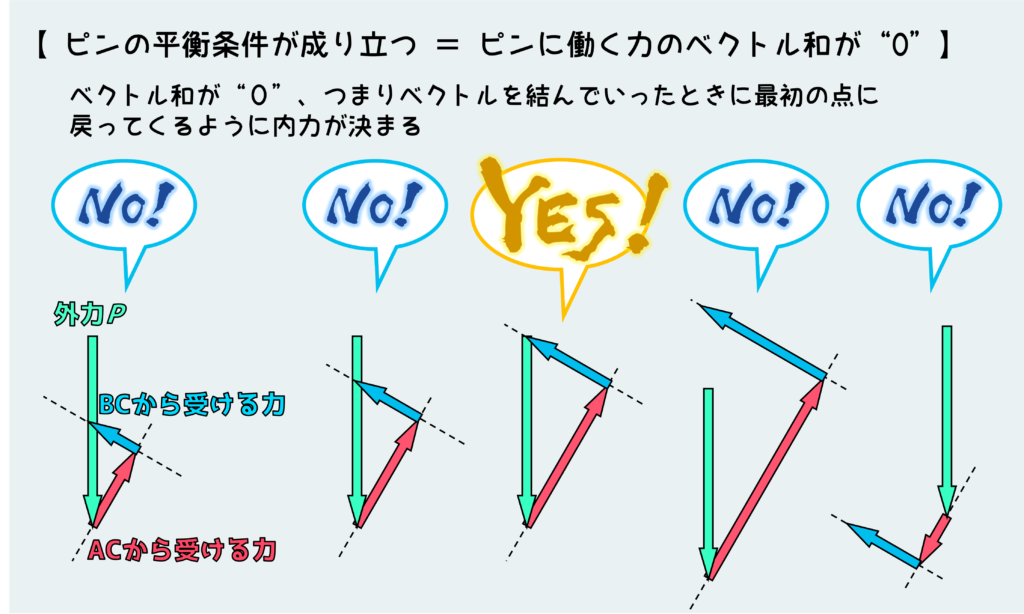
つまり、ピンの平衡条件が成り立つためには、ベクトル和＝０（ゼロ）となる必要がある。なので、さっきのベクトル和の考え方を利用して、ピンに作用している力（ベクトル）を繋げたときに、最初のスタート地点にぴったり戻ってくるような形にならなければならない。
今回のピンBの場合は、まず外力Pが既知のものとしてある上で、内力２つの方向だけ分かっている状況なので、下の絵のように適当な大きさで矢印を書いてみる。すると、当然テキトーに書くと最初のスタート地点に戻ってこれない（ベクトル和が０じゃない）
うまいこと内力（赤矢印と青矢印）の大きさを調整すると、下の真ん中の絵のようにスタート地点に戻ってくるようなベクトル和を描くことができる。
ベクトル和が０（ゼロ）となる形はこの１パターンだけであり、これを満たすように内力の大きさが決まる（こうならないと平衡条件が成り立たない。）
力の方向（引張か圧縮か）についてもここで最終決定できる。
※ベクトルを繋ぐ順番を変えればベクトル和の三角形の形は変わるが、ベクトル和が０（ゼロ）になるときの各ベクトルの大きさは１パターンしかない。
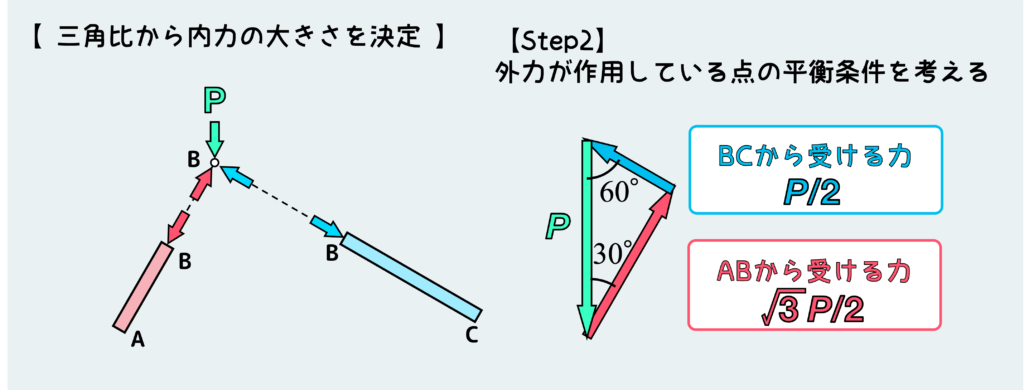
ベクトル和が０（ゼロ）になるような絵を描けたら、あとは状況に応じて三角比などを利用して矢印の大きさ（内力の大きさ）を求めれば良い。
今回は下の絵のように角度が決まっているので、簡単な三角比から青矢印（BCから受ける力）と赤矢印（ABから受ける力）の大きさを決定できる。これらはもちろん、外力P（緑矢印）の大きさを元に計算する。
このようなベクトル和の考え方を使うときは当然丁寧に図を描くことが重要になる。
（どんな問題でもそうだけど）ベクトル和を使うときは丁寧に図を描くことが重要！
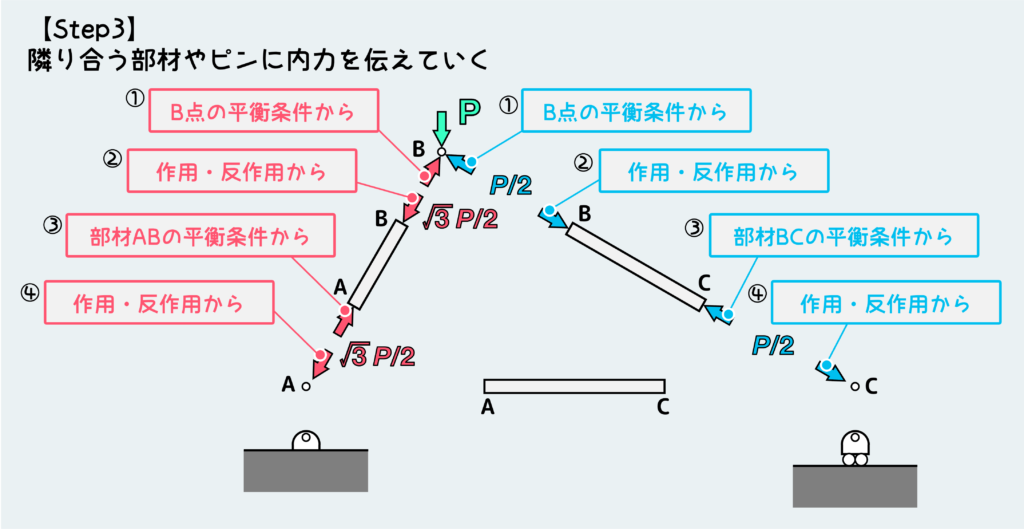
【Step ３】ピンBに働く内力（ABから受ける力とBCから受ける力）が決定できたら、作用・反作用の法則と平衡条件を使って、隣り合う部材やピンに内力を伝えていく。
今回の問題の場合は、下図のように赤矢印はABの方に、青矢印はBCの方に伝わっていく。図中の①〜④は思考の順番である。
赤の方だけ説明すると、まず①ピンBがABから受ける力が決定できたので、②作用・反作用からABには同じ大きさの圧縮力が働くはずで、③部材ABが釣り合うためには反対側（A端）に同じ大きさん圧縮力が働くことになる。さらに④部材ABのA端に働く圧縮力はピンAから受ける力なので、作用・反作用からピンAにも同じ大きさの圧縮力が働く。
という感じに順番にたどっていけば、少しずつトラス構造の中の力の伝わり方が分かっていく訳だ。
さて、ピンBの平衡条件から部材ABとBCに伝わる力は明らかになった。残りは部材ACに伝わる力を明らかにしたい訳だが、次はピンAかもしくはピンCの平衡条件を使っていきたい。
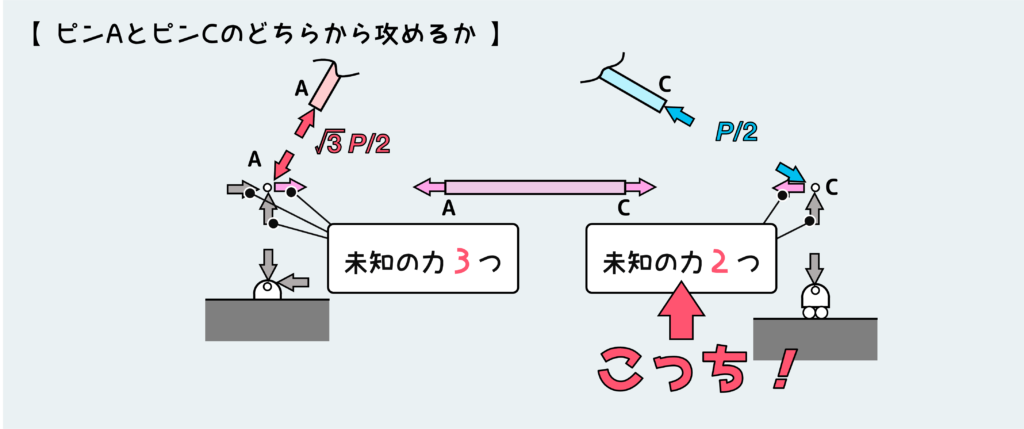
ではどちらのピンの平衡条件を考えるべきだろうか？下の図を見てほしい。
ピンAおよびピンCに働く可能性のある力をひとまずテキトーに書き込んでみる。ピンAの方は、既知のABから受ける力に加えて部材ACから受ける力と支点Aから受ける反力２種の合計３つの力が未知数として残っている。
一方ピンCに関しては、既知のBCから受ける力に加えて部材ACから受ける力と支点Cから受ける反力１種の合計２つの力が未知数である。（以下でもう一度説明する。）
１つのピンの平衡条件から求まる未知数は２つだけである。なぜなら、ピンの平衡条件では回転のつり合いが使えず、力のつり合い２式分の意味合いしか持たないからだ。
という訳で、ピンAの未知の力３つは現時点では決定できない。なのでピンCから攻めていくべきである。
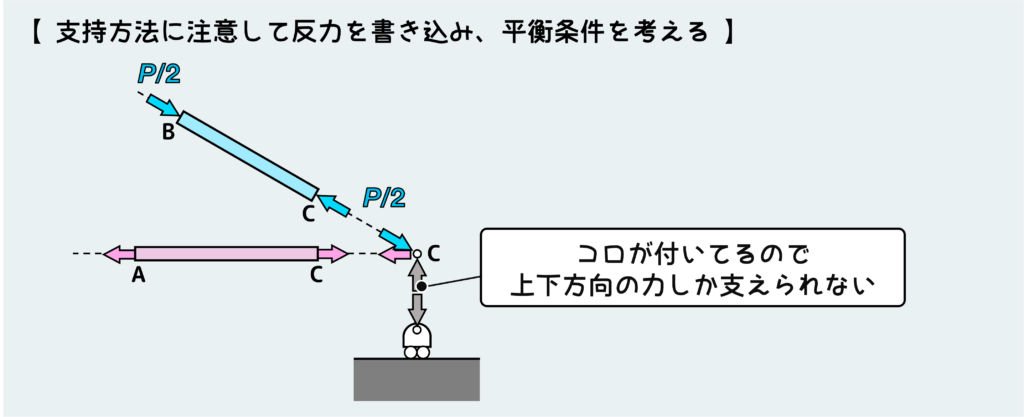
改めてC点を見てみよう。ここでは支点と繋がっているピンの平衡条件を考える際には支持方法に注目しよう。
この支点はピンである上にコロが付いているので、モーメントだけでなく左右方向の力も支えることができない。この支点が支えることができるのは上下方向の力だけである。
なので、ピンCに働く支点からの反力は上下方向の１種となる訳だ。
これに対してピンAの方は上下左右方向の力を支えることができるので、反力は２種となり、未知の力が１つ多いことになる。
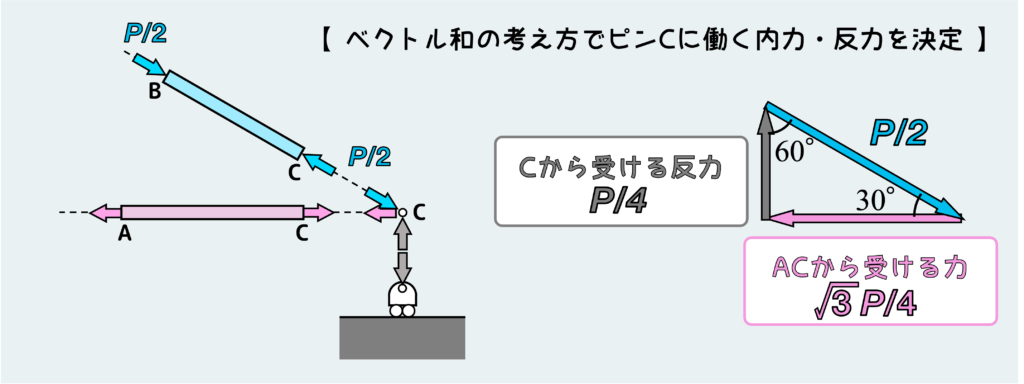
ピンCの平衡条件を考えるときもベクトル和＝０（ゼロ）の考え方を使おう。
部材ACから受ける力（ピンク矢印）と支点Cから受ける反力（灰色矢印）の方向は決まっているので、ベクトル和が０（ゼロ）になるように絵を書くと下のように各力の大きさが決定できる。
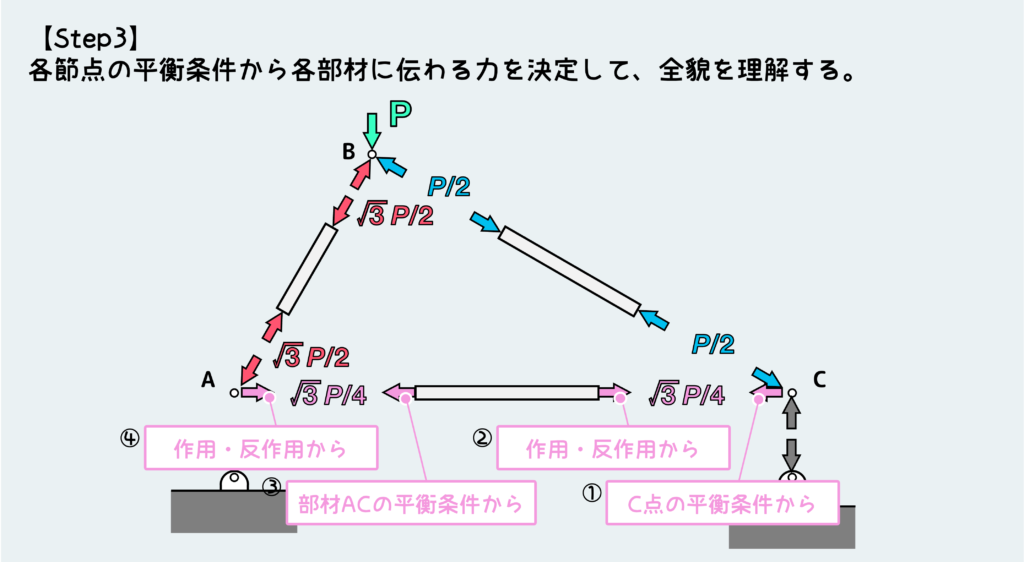
さあここまで分かれば、さらに繋がっている部材へと内力を伝えていけば全体像が分かってくるはずだ。
下図の①〜④を順番に見ていけば分かるだろう。
これで完了だ。このトラス構造の部材に伝わる力は全て明らかになった。部材ABと部材BCは圧縮の力を受けて縮み、部材ACは引張力により伸びる。
例えば各部材に働く応力を問われれば、これらの内力を元に計算できる。もし各点の変位が問われた場合は、ここからさらに考えを進めていかないといけないが、その話はまた別の記事にまとめたいと思う。
ちなみに部材に伝わる力を知りたいだけなら、ピンAの平衡条件はもはや必要ない。しかし、支点Aから受ける反力の大きさが知りたければ、ピンAの平衡条件をさらに考えていく必要がある。
今なら残りの未知数は２つなので、ピンAの平衡条件から支点Aの反力を求めることができる。
まとめ
今回の記事では、トラスの力の伝わり方を節点法により考える方法について丁寧に説明してきた。
苦手な人も多いと思うので、この記事で理解が深まれば幸いだ。
次の記事では切断法について説明していきたいので、そちらの記事もぜひ読んでみてほしい。
材料力学 10分で絶対分かるようになるトラス問題（切断法による力の伝わり方編）【Vol. 3-5】
材料力学 10分で絶対分かるようになるトラス問題（変形量編）【Vol. 3-6】
- トラス部材には軸力しか働かない。これのおかげで強い構造体にできる。
- 各部材に働く内力を明らかにするには節点法と切断法がある。
- 節点法はすべての部材に働く力を明らかにしていき、ある点の変位を知りたい場合に使える。あまりにも複雑なトラスの場合は不向き。
- 切断法は、複雑なトラスの中のある特定の部材に働く内力を知るのに向いている。
- どちらの方法も『切断した自由体の平衡条件を考える』のがポイント！
