材料力学《全員必見・超重要》自由体の考え方（異種材料・別部品）【Vol. 1.2-4】

今回の記事は自由体の考え方の具体例第４弾だ。異種材料や複数の部品があるときの考え方を説明したい。

この記事で伝えたいことはずばり、異種材料や複数の部品があっても、あんまり気にしなくて良いよってことだ。ついつい部品の切れ目や材質の変わり目を気にしちゃうかもしれないけど、力の伝わり方にそんなのは何も関係ない。

この記事で紹介する例で、このことをよく理解してほしい。

その他の具体例（一部執筆中）は以下の通り。

2021年5月13日 材料力学　《全員必見・超重要》自由体の考え方（引張・圧縮を受ける棒）【Vol. 1.2-1】

2021年5月13日 材料力学《全員必見・超重要》自由体の考え方（色んな支持方法）【Vol. 1.2-2】

2021年6月4日 材料力学《全員必見・超重要》自由体の考え方（トラスの問題）【Vol. 1.2-3】

2021年6月22日 材料力学《全員必見・超重要》自由体の考え方（曲げ・ねじり問題）【Vol. 1.2-5】

自由体の基礎について確認したい人は下の記事を読んでほしい。

2020年10月13日 材料力学　《全員必見・超重要》自由体の考え方の基礎【Vol. 1.1】

複数の部品で構成された構造体

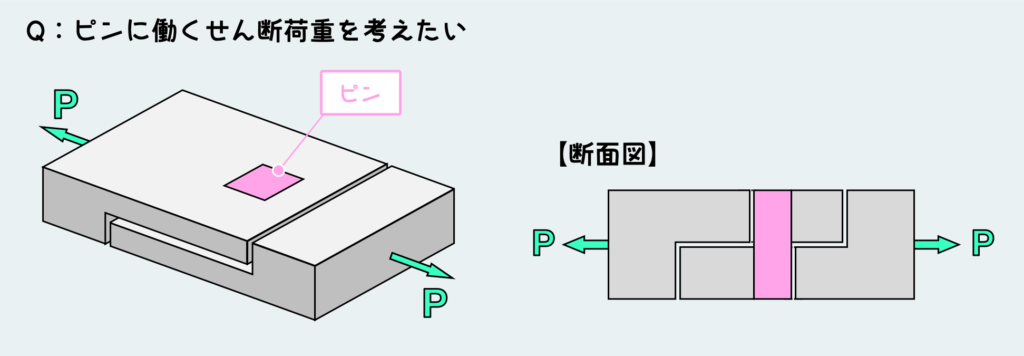
複数のパーツで構成されたものの一例として、上の図のような構造体を考えてみよう。

L字型の板にピン（通常円柱形だと思うが、まああまり気にしないでほしい）を差して接続している。これを両端で引っ張ったときにピンに働くせん断荷重を考えてみよう。

この構造体は、板２つとピンの合計３つのパーツで構成されている。何を考えるにしても自由体を切り出さないと始まらない訳だが、必ずしもパーツ毎に切り分けないといけない訳ではない。パーツ毎に自由体として切り出すと、場合によっては回り道になってしまうのだ。では、一度パーツ毎に自由体に切り分けてみて、いかに面倒な考え方か体感してみよう。

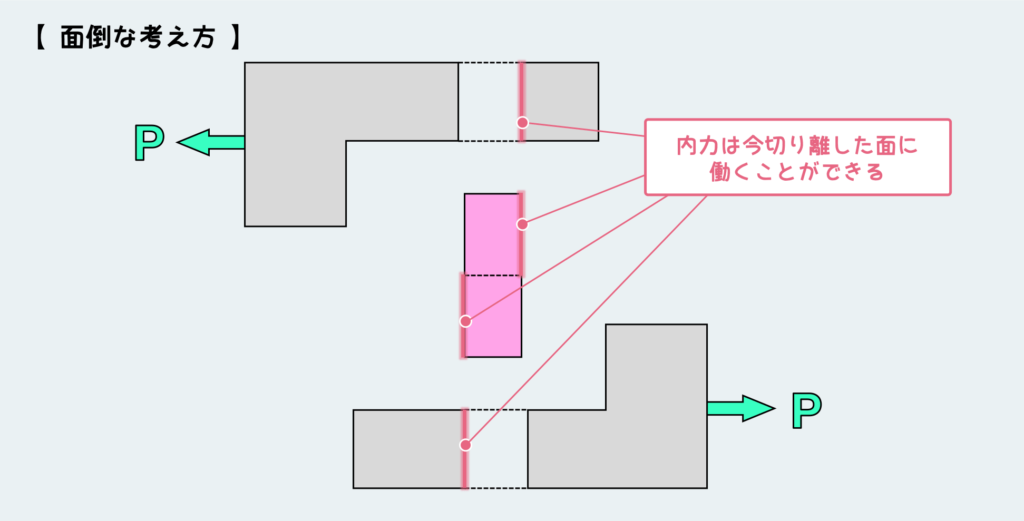
パーツ毎に自由体として切り出したのが上の図だ。

自由体は好きなように切って良いので、こんな風にいくつかの場所を一気に切ってしまうこと自体はルール上問題ない。ここから内力を描き込んでいく訳だが、ここで大事な約束事を思い出そう。それは「内力は切断した面にのみ描くことができる」ということだ。

上図で、赤い線を描いた所が元々繋がっていた（これは物理的に繋がっているという意味ではなく、力を伝えるように接触した状態という意味）部分であり、ここにのみ内力を描き込むことができる。

ピンの平衡条件はこの時点では、何のとっかかりもないので考えられない。まずはL字板から考えないといけない。

L字板の平衡条件を考えると、この図のように内力が決まる。まず横向きの力が釣り合うように、ピンとの接触面に内力としてP（水色）が作用する。

モーメントに関しては、この内力Pがどういう範囲に働くか（接触面全体に一様に作用するのか、接触面の最下部の所に局所的に作用するのか）によって変わるので、ここではモーメントの大きさには触れないことにする。とにかく、外力のP（緑色）と内力のP（水色）の作るモーメントにバランスするように内力としてモーメントが働くことになる。

さてこの内力は何から受けた力かと言うと、もちろんピンだ。ピンがこの板を押している訳だ。

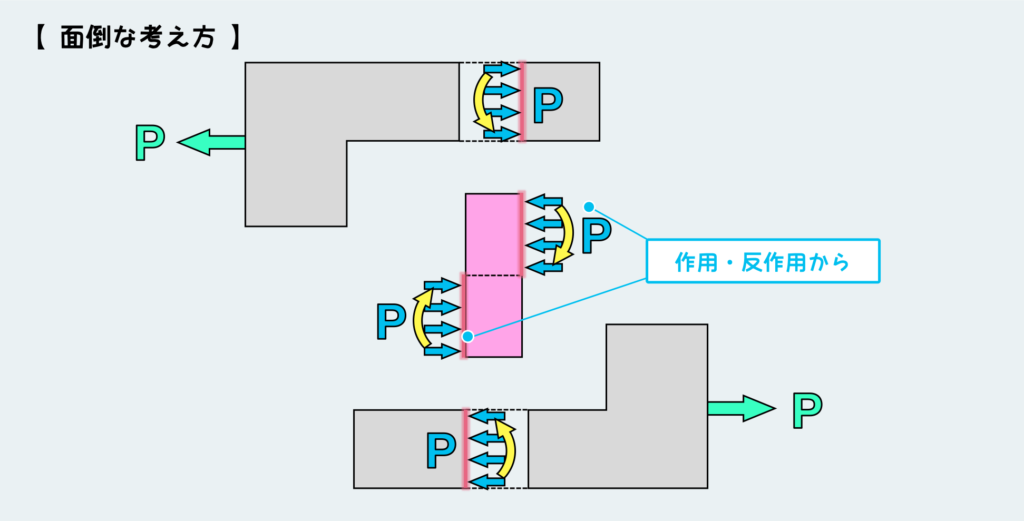
てことは、作用・反作用の法則からピンの方は同じだけの内力（反対向き）を受けることになり、ピンには上図のように内力が働いていることが分かる。

ピンの平衡条件は取れるのか？と疑問に思う人もいるかもしれないが、これは心配無用だ。ピンのバランスは必然的に取れてしまう。上の板から伝わってくる内力も、下の板から伝わってきた内力も、元々外力のPとバランスするものなので、上下から別々に伝わってきた内力同士も当然バランスが取れる訳だ。

ようやくここから、肝心のピンに働くせん断荷重について考えよう。ピン中央の横断面に最大のせん断荷重が作用することはなんとなくイメージできるだろう。上半分は左に行こうとして、下半分は右に行こうとするので、その境目に最大のせん断荷重が作用する。（内力Pの分布の仕方によって、どの部分にまでせん断荷重が働くかは変わるが、いずれにせよ中央の横断面に最大せん断荷重が作用する。）

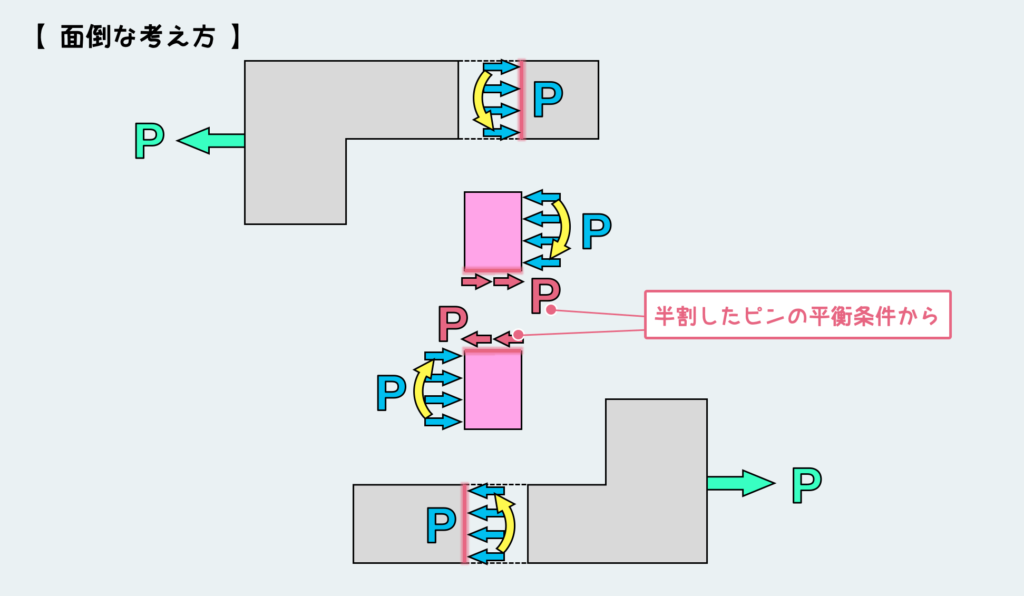
という訳で、ピンの中央の断面でさらに切断して、自由体図を描き直そう。そうすると上のようになる。

ここまで明らかになった内力については、そのまま描き込めば良い。さらに今切断したピンの横断面に内力が作用することになる。半割りしたピンの平衡条件を考えることで、ここの内力は明らかになる。

結果としては、ピン中央の横断面には外力と同じ大きさのせん断力Pが作用していることが分かる。しかし、ここまでの道筋を振り返ってどうだろうか？こんな簡単なことを知るのに、ずいぶんと回りくどい道のりを歩いてきたと感じないだろうか？

実際その通りで、こんなに面倒な手順を踏まなくてもこの結論は得られるのだ。

スマートに考えるために基本に立ち返ろう。前の記事でも説明した通り、自由体を切り出すときは「知りたいものがある所で切る！」これが大事だ。今知りたいのは、ピン中央の横断面に働くであろう最大せん断荷重だ。なので、素直にピン中央の横断面で切断した自由体図を描こう。

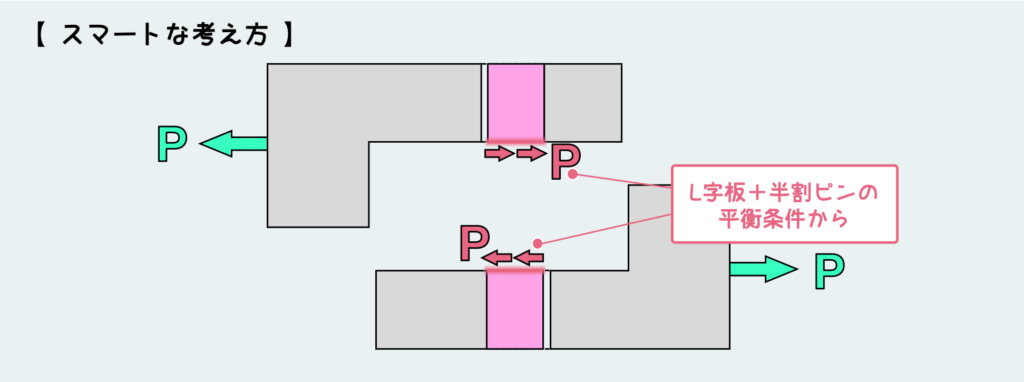
ピン中央で切断すると、上のように自由体図を描くことができる。

今切断した部分（上図で赤い線を引いた場所）にしか内力は働かないので、これを元にL字板＋半割りピンの平衡条件を考えると、このピンの横断面に働く内力はせん断力Pだと決定できる。

当たり前だが、上で説明した面倒な考え方のときと結論は変わらない。しかし、今回の方がはるかに直接的なアプローチだと感じるだろう。

このように、複数のパーツで構成されていても、必ずしもパーツ毎に切り分けないといけないなんて事はない。基本を思い出して「知りたいものがある所で切る」ことで効果的に内力の伝わり方を導き出すことができる。

圧力容器に関する特別な考え方

上で説明した通り、複数のパーツで構成されていても、あるいは異種材料の組合せだとしても、材料の境目で切らないといけないなんてことはなく、素直に知りたいものがある部分で切れば良い。

これの特殊な例として、「圧力容器」を考えてみよう。

圧力容器を安全に設計するためには、ガスだとか液体だとか圧力をかけて流体を封入したときに、容器に生じる応力を理解していないといけない。やる事はこれまで同じ、自由体の平衡条件を利用して力の伝わり方を把握する。

上図のような円筒型容器を考えよう。円筒型のときの考え方を理解すれば、これが球形タンクになっても問題ないはずだ。（※ちなみに通常材料力学で扱うのは「薄肉」の圧力容器であり、厚み方向の変化を考慮しないような簡単化したモデルだ。厚み方向の変化を考慮するような問題では、よりややこしい計算が必要になる。）

圧力容器に生じる応力を考える前に、知っておいてほしい重要なことがある。それは静水圧（応力）についてだ。

一様な圧力を受ける流体の力学状態を絵に描くと下の図のようになる。こういう風に、三次元的にどの方向からも一様に作用する圧力（応力）のこと（もしくはその状態のこと）を静水圧という。この流体の中から小さな要素を取り出してみると、どこから・どんな方向の面を取り出しても、その断面には外から受けている圧力と等しい大きさの圧力が作用する。

これは非常に重要な特徴だ。

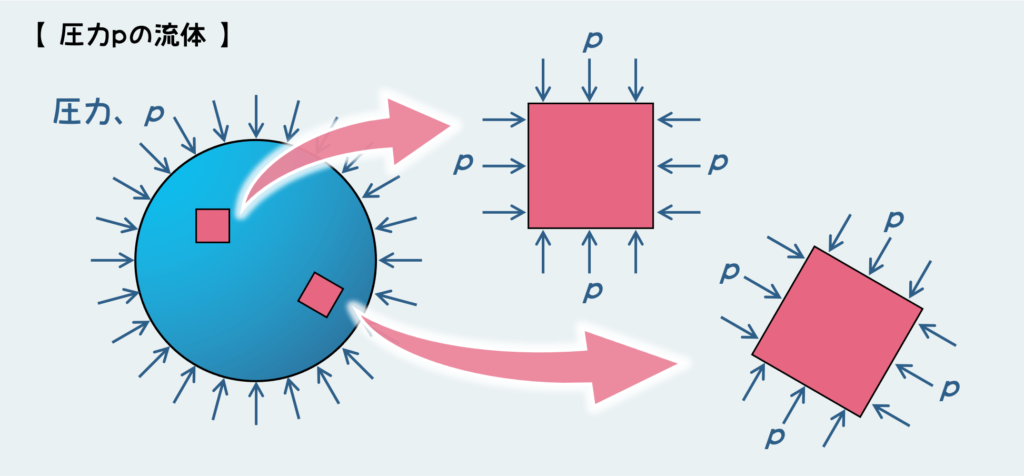
このことは何も流体に限った話ではない。いかなる材料でも静水圧下ではこの特徴が働く。深海に沈んだ金属片を思い浮かべてみよう。

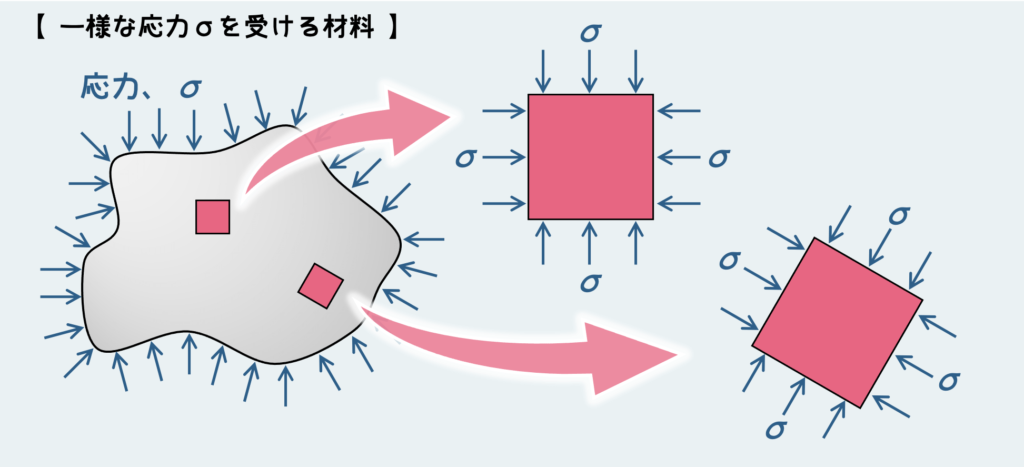
つまり下図のように、材料の外部から一様な圧力（応力）が働くとその内部では、どこの・どの方向の断面にも外部から働いている応力と等しい応力が働く。ちなみに静水圧は基本圧力の話なので、圧縮応力のことを指すが、この特徴自体は引張応力でも同じように成り立つ。何だったら三次元的に一様な引張応力が作用している状態も静水圧と言うこともあるし、人によっては逆静水圧とか言うこともある（気がする）。

なんでこんな事が起こるかっていうのは、応力変換（断面の方向を変えたときに作用する応力が変わる）の考え方を学べば分かる。が、その話はまた今度にしよう。

さあ圧力容器の話に戻ろう。

容器内には静水圧状態の流体が詰まってる。この流体は時には無味無臭で目で見ることもできないが、確かにそこに存在し、力を伝えている。つまり何が言いたいかというと、流体だって力を伝えることができる立派な材料だってことだ。

じゃあこの容器のある断面に作用する力、さらには応力を理解するために自由体として容器を切断するとしたら、最も直接的で素直な切り出し方はどんな方法だろうか。

上で説明した、ピンが受けるせん断荷重の話を思い出してみよう。最も直接的なアプローチは、複数の材料や異種材料があることは気にせず、知りたいものがある部分でシンプルに切り出すことだ。

さっき言ったように、中身の流体も立派な材料なので、この流体も材料としてまるごと切断するのが良い。軸方向応力（軸方向に垂直な断面に作用する応力）σ_aを知りたければ、下図のように中身の流体ごとズバッと自由体を切り出す訳だ。

中身の流体の断面（水色の面）には、内圧と等しい圧力（応力）pが作用している。これはさっき説明した通り、静水圧状態の流体はどこをどう切っても圧力と等しい応力が作用するからだ。

そして、これに釣り合うようにどこかに内力が働く必要があるが、もちろん働く場所は容器断面（赤色の面）しかない。

したがって、流体断面に作用する圧縮応力pによる力と、容器断面に作用する軸方向応力σ_aによる力がバランスするようにσ_aが決定される。

圧力や応力は「力」ではないので、平衡条件式にそのまま入れることはできない。それが作用している断面の面積をかけることで「力」にしてやらないといけない。

なので上に書いてる通り、平衡条件式を立てることができ、結果として内圧pを受ける円筒型圧力容器に作用する軸方向応力σ_aは “Dp/4h” と表せる訳だ。

次に、周方向応力について考えてみよう。やり方は同じだ。

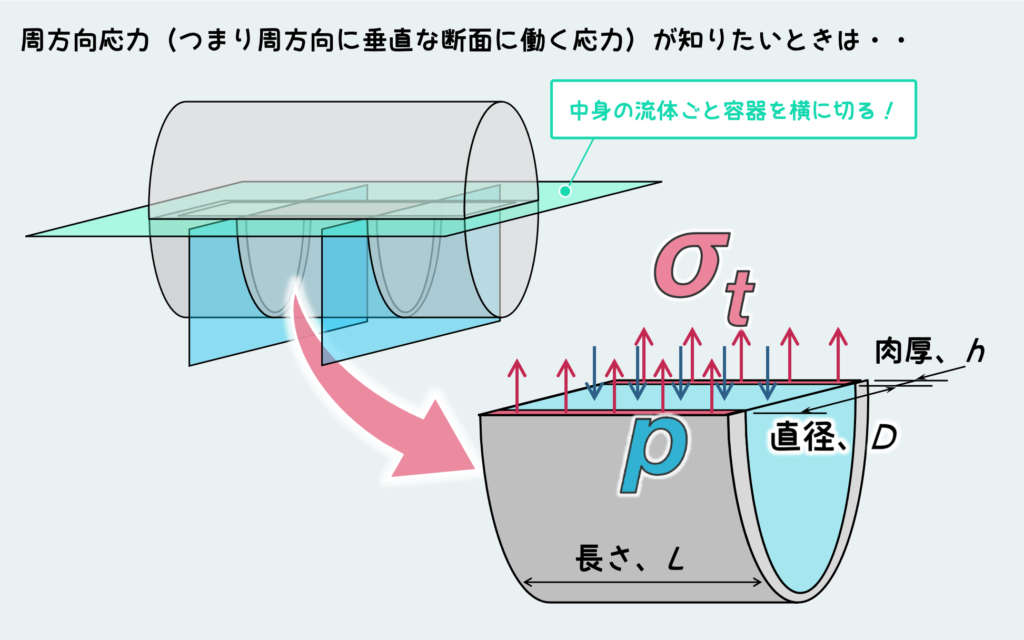
周方向に垂直な断面を含むように、ずばっと横に切断すると上のようになる。今考えたいのは容器胴部の周方向応力なんだけど、ただ横に切っただけだと胴部以外の部分（両端の蓋の部分）も含んじゃってややこしくなるので、横に切った後胴部の一部を切り出すように縦にも切ろう（長さLのかまぼこ型の自由体を切り出す感じだ）。

この自由体にはどんな力が働くか。まず今切った流体断面（水色の面）には、やはり内圧と等しい圧力（応力）pが作用している。しかし、これだけだと釣り合いが取れないので、これに対抗するように容器断面（赤色の面）に引張応力が働く必要があり、これが周方向応力σ_tだ。

※なお、この自由体ではもちろん両横の断面（半円形状の部分）にも圧縮応力pや軸方向応力σ_aが作用するが、絵がぐちゃぐちゃになるので省略している。心配しなくてもさっき軸方向応力の所で考えた通り、こいつらはちゃんとバランスしてくれるので、この自由体の水平方向の平衡条件は満足する。

周方向応力の大きさは、上のように立てた平衡条件式から求まる。軸方向応力のときと同じで、応力に面積をかけて「力」にしてから式を立てることを忘れないようにしよう。

結論として、内圧pを受ける円筒型圧力容器に作用する周方向応力σ_t = “Dp/2h” が得られる。

さて、この記事では一貫して、複数のパーツや異種材料が混ざってても気にするな、そのまま素直に知りたいものがある所を切ればいいんだと言ってきたけど、圧力容器の問題で別のアプローチをしたらどうなるだろうか？

つまり、中身の流体は別物として考えて、あくまで容器だけを自由体として切り出して、軸方向および周方向に作用する応力を導き出そうとするとどんな困難が待ってるだろうか？

そういう事をやろうとすると、自由体図は上図のようになる。

まあ、軸方向応力の方は結果として平衡条件式を導き出すのに考える道筋は同じで、大して変わらないように感じるだろう。

一方、周方向応力の方は一気に難しくなる。上図のように、圧力pが曲面上に一様に分布する形になるので、力を計算する際にpを積分しなくてはならなくなってしまう。

まとめ

この記事で紹介した２例とも、非効率的な自由体の切り出し方（別部品をすべてバラバラに切り出したり、圧力容器の中身の流体を別物と考えて容器だけを切り出したり）をしても、最終的に答えは導き出せる。

自由体の切り出し方はまさに自由で、どんな切り出し方をしたとしても正しく考えれば、正しい姿が得られる。しかし、ややこしい切り出し方をするとそれだけ正しく考えるのは難しくなってしまう。

大事なことは、素直に知りたいものがある部分で切る、ということだ。別の部品や材料をまたがったとしてもそんなの気にする必要はない。ズバッとシンプルに切ろう。