このブログには「広告」を含む記事があります。
これまでの記事で自由体図の描き方について説明してきたが、この記事ではよくやりがちなミスを紹介しようと思う。
基本的な描き方を学んだはずなのに、ついついやってしまう失敗例をいくつかまとめたのでサラッと読んでおいてほしい。
どの失敗も一度知っておけば何てことないような事、ちょっとした勘違いのせいだ。てことは、こんな何でもないことで点数を落としてしまうのは非常にもったいないことだと言える。しかも自由体図を描くのはたいてい解答の序盤なので、このミスのせいで1つの問題すべてを落としてしまうこともあり得る。なんて恐ろしいことだろう。
そんな事にならないようにぜひご一読いただきたい。
自由体図って?て人はこの↓記事を先に読んでほしい。
 材料力学 《全員必見・超重要》自由体の考え方の基礎【Vol. 1.1】
材料力学 《全員必見・超重要》自由体の考え方の基礎【Vol. 1.1】
描き方のいろんなパターンを知りたい人はこれら↓を確認しよう。
- 剛体は「荷重がかからない材料」ではない!「どんなに負荷がかかっても変形しない材料」だ。
- 静定問題である限り、自由体図および内力の決定するときに材質を気にする必要はない。不静定問題では変形の条件が必要になるので、材質も関係してくる。
- 発生する可能性のある内力はすべてもれなく描き込むことが大事。その上で、平衡条件から存在しないと分かったときに初めて、その内力を自由体図から消すことができる。
【勘違い1】剛体には力が伝わらない??
問題でよく「この部材は剛体とする」みたいな設定を目にすることがあるだろう。1つ目の失敗例はこの剛体に関するものだ。
剛体とは何かというと、一言でいうと「どんなに負荷が作用しても一切変形しない材料」のことだ。
材料の変形のしにくさを表すパラメータとして剛性というものがあるが、剛体は剛性が無限大に大きな材料で、全く変形しないと考えることができる。
まあ現実にはそんな材料存在しないと思うが、工学的には剛体とみなして問題を解いた方が都合が良いことがある。工学の世界では複雑な問題をより簡単なモデルと置き換える(みなす)ことが重要なスキルであり、そしてそれが工学者のセンスだ。もちろんモデル化することで厳密な解は得られないが、実用上十分な精度で未来を予測することができる。
では剛体がどんなものか分かったところで、剛体に関連する失敗例を紹介しよう。
下のような問題を考えてみよう。壁につながった2本の棒(ABとCD)の先端を板で接続しており、この板に荷重Pをかけて引っ張っている。2本の棒の一方(AB)は剛体であり、もう一方(CD)はヤング率Eの鋼製だ。このとき、それぞれの棒に働く荷重と先端の板の移動量を求める。
(ただし、先端の板は傾かずにまっすぐ右方向に動こうとするものとする。)
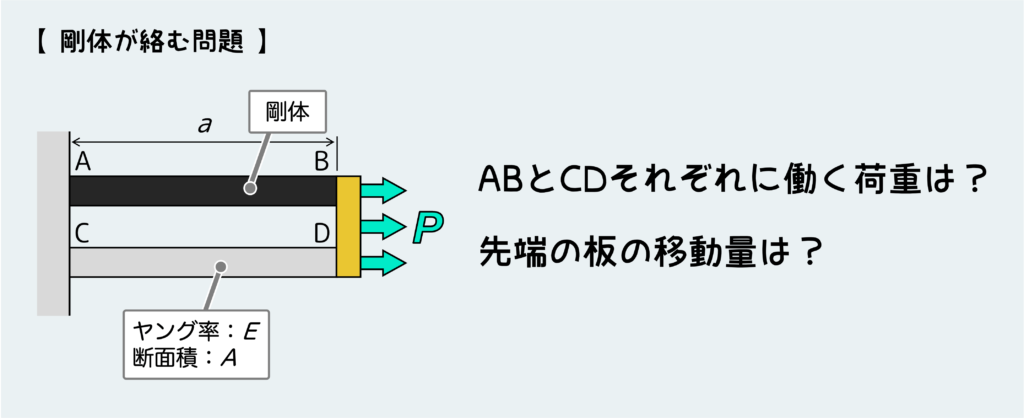
さて、解けただろうか?
ものすごく簡単な問題なので、頭の中でもすぐに答えが出ていないといけない。
では、まずやりがちなミスを紹介しよう。これだ。
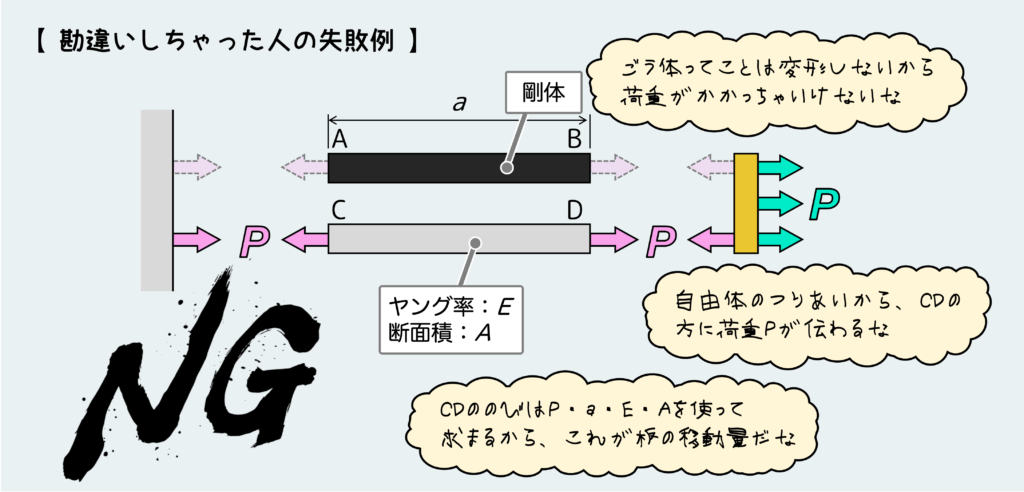
ここで起きている勘違いは『剛体は変形しちゃいけない、ってことは荷重もかからない』だ。そんな訳ない!
剛体が変形しないのは、荷重がかからないからじゃない。剛性(弾性係数)が無限に大きいからだ。だからつまり、荷重はいくらかかってもいいのである。
見ての通り上の回答例では、結局剛体が変形してしまっている。最初の『剛体は変形しちゃいけない』が破綻しているじゃないか。ここで「おかしいぞ」と気付ければまだマシだが、答えが出たことに満足して素通りしてしまう人も少なくない。
正しくはこうだ。
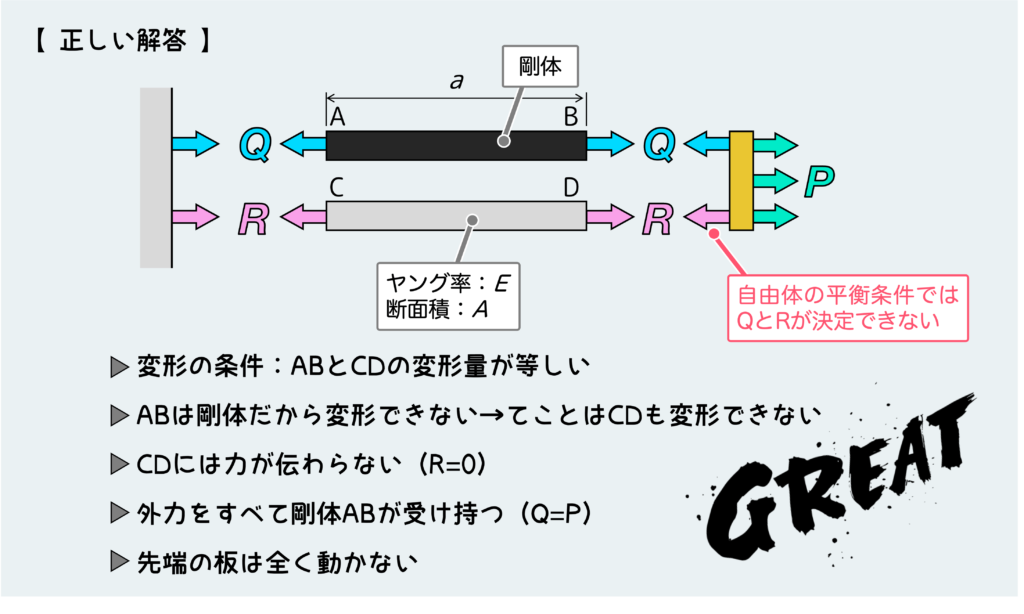
このように、剛体が変形しないことは剛体に伝わる力とは何の関係もないので、ちゃんと剛体にも内力を設定しないといけない。この問題の場合は不静定問題なので、剛体が変形しないという条件を使う必要がある。つまり、鋼製のCDも変形することができないので、CDに伝わる内力は”0”ということが分かり、結局外力として加えた荷重Pを剛体ABがすべて受け持っているということになる訳だ。もちろん先端の板の移動量は”0”だ。
ちょっとした勘違いがいかに変な答えを導き出してしまうか、実感できたと思う(だって真逆の答えになっちゃうんだから・・)
材質について
今回は剛体を例に出したが、自由体図を使って内力の伝わり方を考える際には基本的に材質を気にする必要はない。
つまり、異なる数種類の材料で構成されたもの(こっちがアルミでこっちが銅みたいな)でも、アルミとか銅とか気にせず自由体図を描いて、内力の伝わり方を決定していけば良い。
ただしこれは静定問題の場合だ。
不静定問題のときは、内力を決定するために『変形の条件』が必要になってくるので、変形量も考えないといけなくなる。変形量にはもちろん材質が関係するので、不静定問題の場合はちゃんと材質の違いを考慮に入れて考えていかないといけない。
【勘違い2】外力としてモーメントが加わるなら、発生する内力はモーメントだけ??
ここから紹介する2つの例はどちらも、自由体に描き込むべき内力の種類を勝手に変えてしまった間違いだ。
まずはこの例を見てほしい。
壁に片側を完全固定支持されたはりをワイヤーで吊っており、先端にモーメントが作用している。このとき、壁から受ける反力を求めよう。

では、早速失敗例を見てみよう。
この失敗を引き起こしている勘違いは『外部からモーメントが加わってるんだから、これによって発生する内力や反力もモーメントでしょ』だ。こういうミスは結構多いと思う。一応釣り合いはとれるので、一見合ってるように見えてしまうのだ。
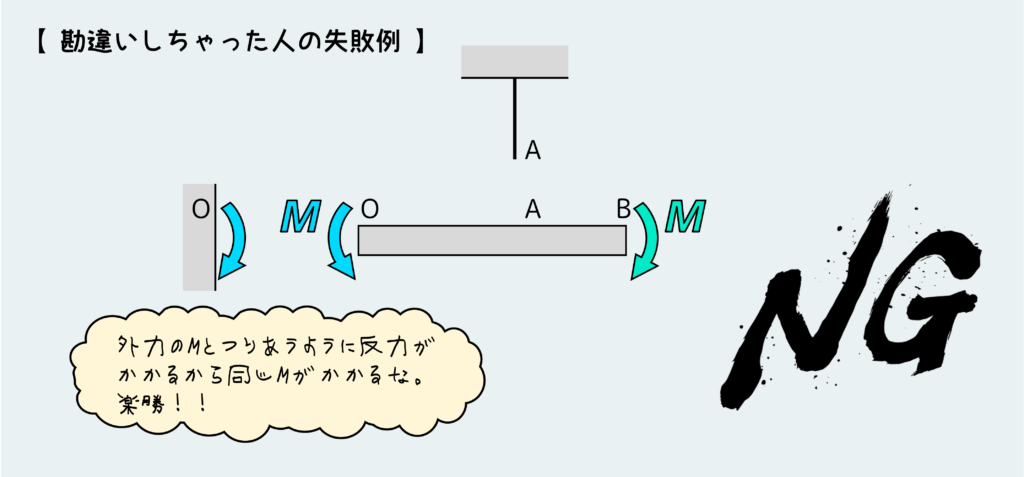
こういったミスを防ぐためには、発生しうる内力は全部描き込むこと、変形後の状態を正しく想像することが重要だ。
正しくはこう。じっくり見ていこう。
まず壁の支点では完全固定なので3種類の反力すべて(Rox、Roy、Mo)が発生する可能性がある。描き込む内力を勝手に減らしてはダメだ!減らしてもいいのは、平衡条件を考えて、それが働かないことが分かったときだけだ。
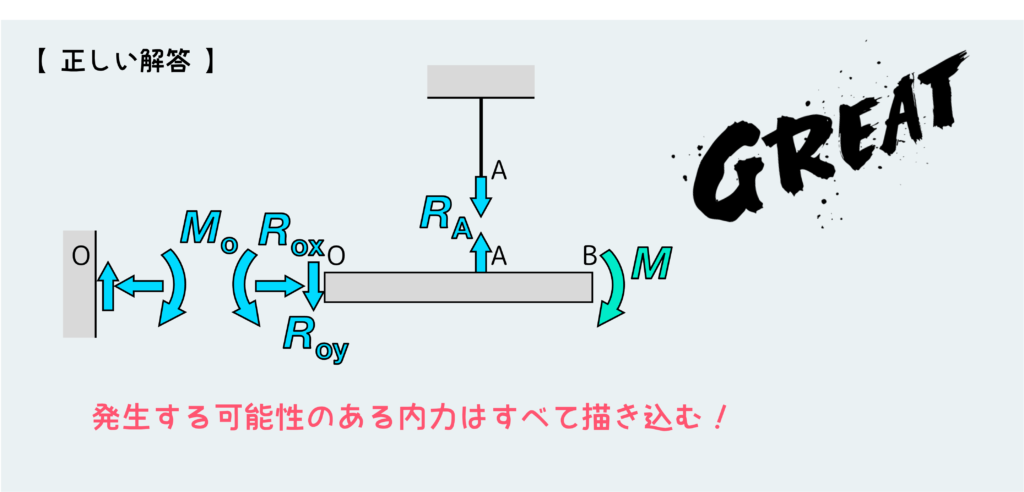
さらに変形後の状態をしっかり想像すると、このはりは外力を受けて下方向にたわむことが分かるだろう。ワイヤーもA点でつながってるので一緒に伸びる必要がある。てことはワイヤーには何かしらの引張荷重(RA)が作用しなくてはならない。そうなるとこのはりの自由体にはワイヤーから受ける上方向の荷重が働くので、これと釣り合う下方向の荷重がどこかに働かないといけない。それはどこか?
壁しかない。つまり、Roy=RAとなるような反力を壁から受けることになる。
ここから先は不静定問題であり、詳細は省く。流れとしては、ワイヤーの伸びとはりのA点のたわみ量が等しいという条件を使ってRAが決まる。つまり、壁から受ける反力Royも決まる。
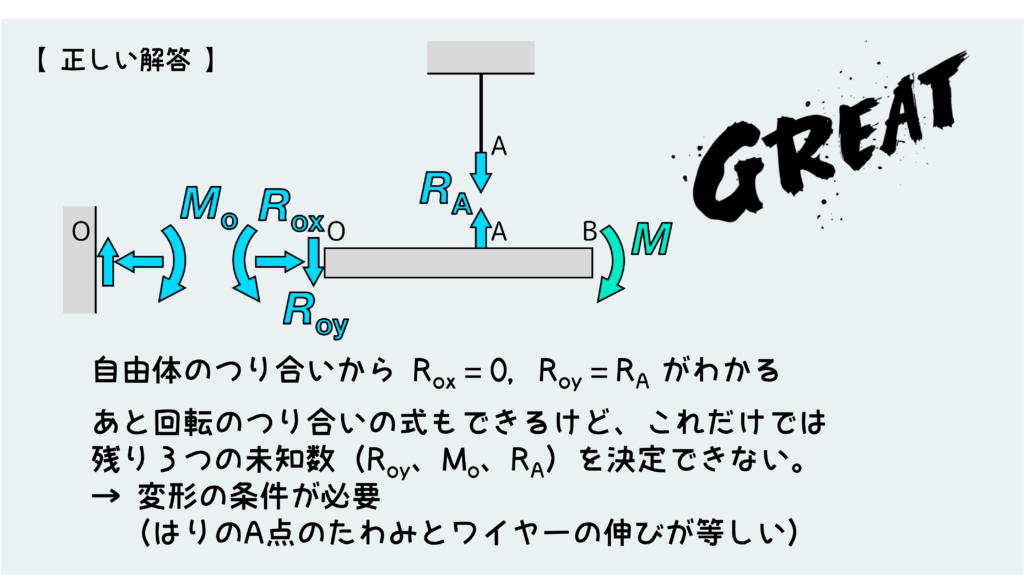
このように、外力の種類から安直に内力の種類を決めつけるのは絶対にやってはダメなことだ。ちゃんと平衡条件を踏まえた上で、内力があるかないか、その大きさなど判断していかないといけない。
ちなみにもしワイヤーがなければ、はりに描き込む力は壁から受ける反力3種で終わりなので、平衡条件から結果的に壁から受ける反力はモーメントMoのみとなる。(Rox=Roy=0)
【勘違い3】外力として荷重が加わるなら、発生する内力は荷重だけ??
次の例も、さっきの例とほとんど同じパターンだ。
さっきとは逆に、外力が荷重だから内力(ここでは反力)も荷重しかないと決めつけて、モーメントの存在を忘れてしまった例だ。(個人的には、さっきの例のような内力としての荷重を忘れるパターンよりもあり得そうな気がする)
こういう問題だ。
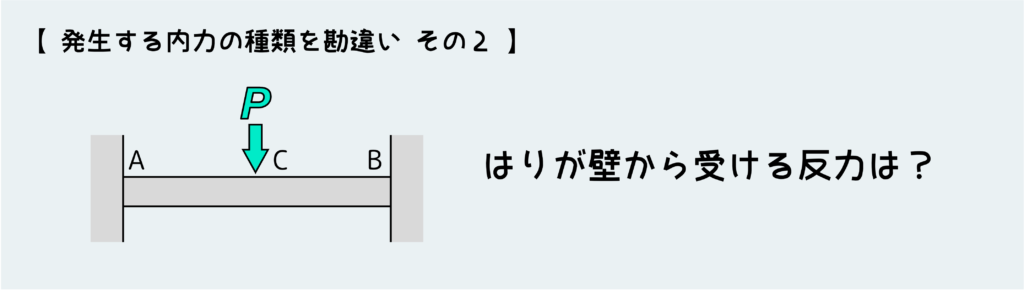
両端固定のはりABの中央C点に荷重が作用しているとき、このはりが壁から受ける反力を求めよう。
反力を求めたいのだから当然、はりだけを自由体として取り出してきて平衡条件を考える、という流れになるだろう。
問題は、自由体に対して正確に内力を描き込めるかということだが、これができるかどうかで全く違う問題になってしまう。
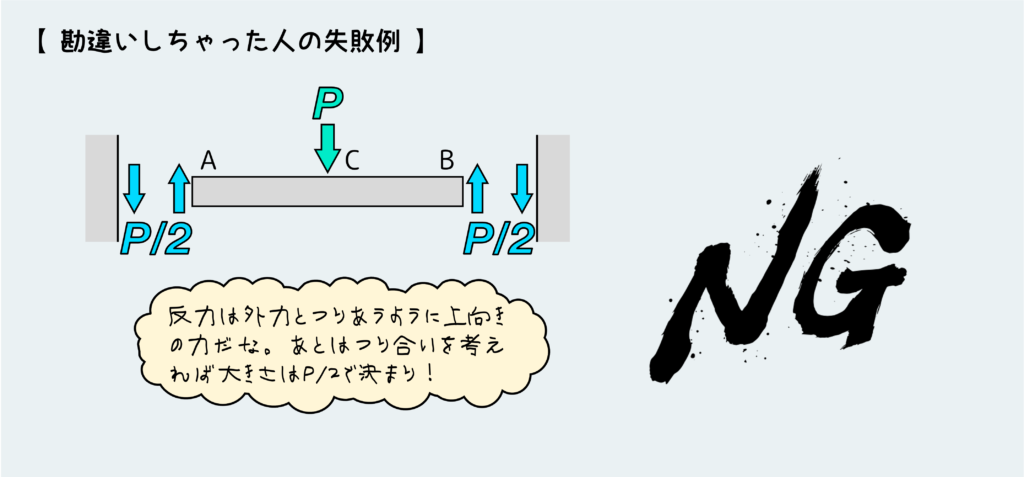
では、まずダメな例だ。
この失敗例では、さっきの例と同じく、外力の種類が荷重だからといって内力も荷重だけだと短絡的に思い込んでいるのが敗因だ。モーメントの存在を忘れてしまっている。
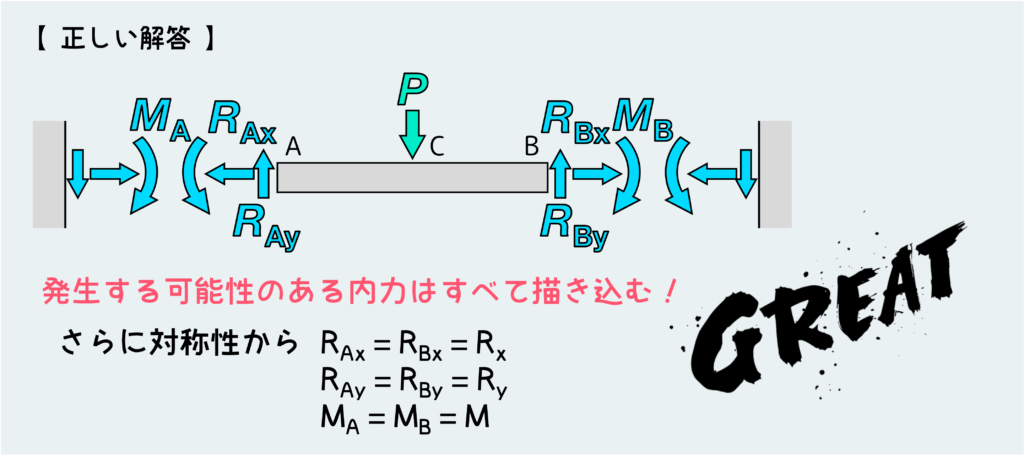
ここまで読んでくれた人たちはもう分かると思うが、正しくは下のようになる。
この問題でははりが両端固定なので、壁から受ける反力は3種類すべて発生しうる。なので、図のようにすべての反力を描き込んでから平衡条件を考えなくてはならない。さらに、この構造の対称性からAとBでそれぞれ発生する反力は同じである(RAx=RBx=Rx、RAy=RBy=Ry、MA=MB=M)
これらに対して平衡条件式を立てる訳だが、やってみれば分かるが、平衡条件だけではこの3種のうちRy(=P/2)しか決定できない。つまりこれは不静定問題なので、変形の条件を使って反力を決定する必要がある。
まず、水平方向には変形しないので、水平方向反力は存在しない。(Rx=0)
厳密には無いってことはないかもしれないが、曲げを引き起こしている曲げモーメントや縦方向の力と比べて重要ではない。
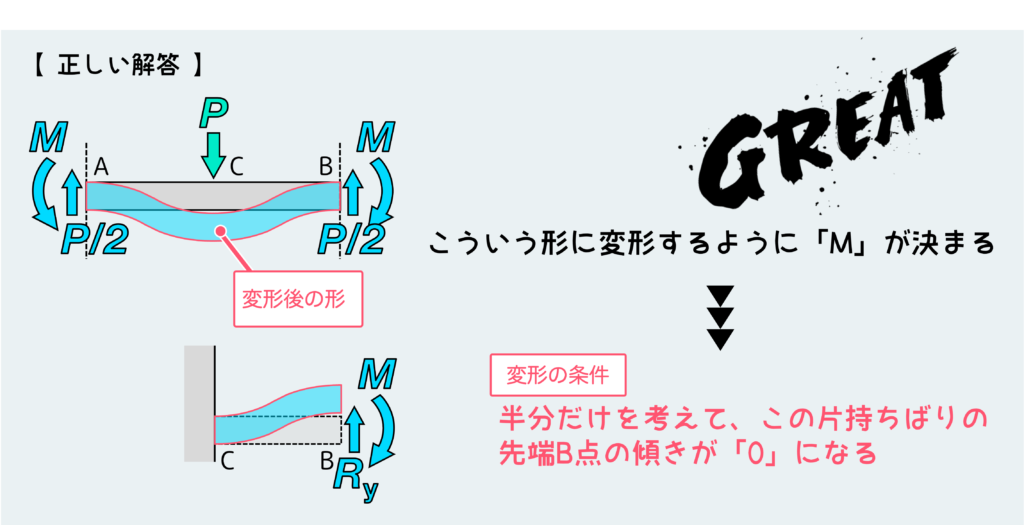
次に、モーメントMを決定するための変形の条件はこのように考えれば良い。中央のC点を仮想的に固定端にして片持ちばりを想定し、B点に作用する反力による変形を考える。実際にはB点は壁で完全に固定されているので、B点の傾きが0になるような反力Mを求めればいいってことだ。
ところで上で紹介した失敗例だが、これが正解になるような問題もある。それはこれだ。
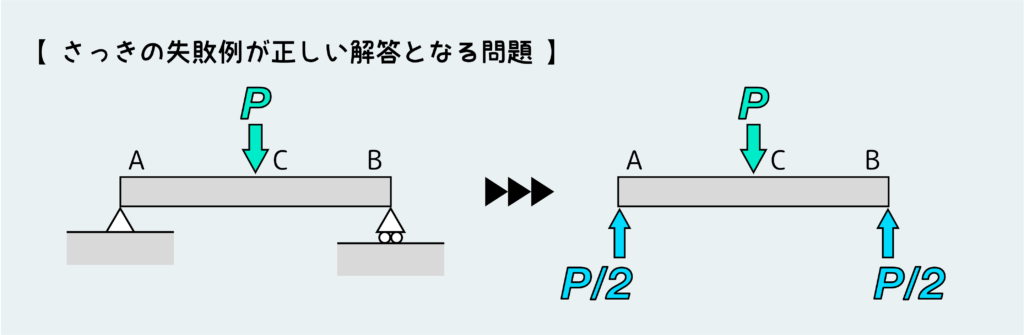
この問題の場合は、支点A、Bが単純支持(ピンやナイフエッジのような回転を拘束しない支持方法)なので、ここに発生する反力は縦方向の荷重のみということになる。
水平方向荷重に関しても、B点の支点にコロが付いているので、水平方向荷重を支えることができない。したがって、この問題であれば、上で紹介した失敗例で正解であり、静定問題なのですごくシンプルに解けてしまう。
このように、自由体図は正しく描けないと全く別の問題を解いているようなことになりかねないので、しっかり理解して正確に書けるように気を付けよう。
- 剛体は「荷重がかからない材料」ではない!「どんなに負荷がかかっても変形しない材料」だ。
- 静定問題である限り、自由体図および内力の決定するときに材質を気にする必要はない。不静定問題では変形の条件が必要になるので、材質も関係してくる。
- 発生する可能性のある内力はすべてもれなく描き込むことが大事。その上で、平衡条件から存在しないと分かったときに初めて、その内力を自由体図から消すことができる。