この記事では、せん断応力が問題になる現象の代表選手・ねじり問題について解説する。
ねじりというのは引張・圧縮とは少し違い、イメージしにくいと感じている人も多いかもしれない。この記事で、ねじりを受ける材料の変形と応力状態の特徴をつかんでもらえばと思う。
ねじり以外でせん断応力が登場するケースである『ピンやリベット接続する部材』の話は別記事で解説しているので、ぜひそちらも合わせて読んでほしい。
材料力学 ピンやリベットが受けるせん断応力の考え方【材力Vol. 4-1】
- ねじり（トルク）を受ける材料の横断面には、位置に関係なく外力と同じ大きさのトルクが伝わっている。
- ねじりを受ける部材の横断面にはせん断応力が発生し、中立軸上では応力“0”で、中立軸から遠ざかるほど（半径rに比例して）せん断応力は大きくなる。
- せん断応力を求めるには極断面二次モーメントが必要。
今ならebookjapanで超お得クーポンがもらえる！
漫画をお得に読むなら『ebookjapan』がオススメです。電子書籍なら、スマホさえあればいつでもどこでも好きな漫画が読めますし、本棚を常に持ち歩いているようなもので非常に便利です。
また、『ebookjapan』なら初回ログインクーポンだけでなく、頻繁にクーポンを配布していますので、タイミングがあえばめちゃくちゃ安く漫画を手に入れられます。ぼくも先日ある完結作品およそ20,000円の漫画を半額で手に入れちゃいました。
「読みたい漫画がないな」という人は下の記事で僕のオススメ漫画を紹介してますので、ぜひ覗いてみてください。
今なら12/5まで3700作品以上のオススメ作品対象の50%OFFクーポンが配布されています！なんと期限まで金額の制限なく半額になってしまうという超絶お得クーポンです。たとえば下のような作品が全巻半額でGetできます！（もちろん全巻じゃなくてもクーポンを使えます）
21,120円
→ 10,560円
17,424円
→ 8,712円
20,856円
→ 10,428円
13,728円
→ 6,864円
ebookjapanはこちら！
僕のオススメ漫画はこちら！
Contents
ねじりによるせん断応力
ねじり変形とはどういうものか？
引張・圧縮とは違いなかなかイメージしにくいかもしれない。なぜなら目に見える変形をしない（形状の変化として図に描けない）からだ。
そんな人は『雑巾絞り』を思い浮かべてほしい。雑巾絞りをしたことない人なんていないだろう。
雑巾絞りのような負荷が“ねじり”だ。分かりやすいように色を付けているが、こういう変形をするというのを常に頭に入れておいてほしい。
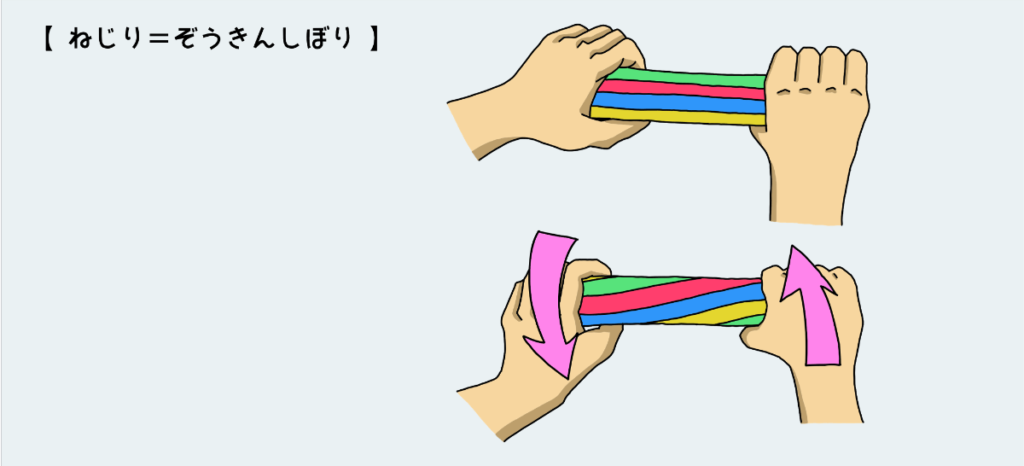
さて、この雑巾絞りを頭に入れた上で、もう少し詳しく見ていこう。
棒の表面に描いた線がどのように動くかに着目し、どのような変形が起きているかを理解しよう。
下の図で描いている通り、ねじり変形で起きる変化は『面が回転する』ことである。
（このように線を描いておかないと変形がぜんぜん見えない。そこが引張・圧縮との違いだ。）
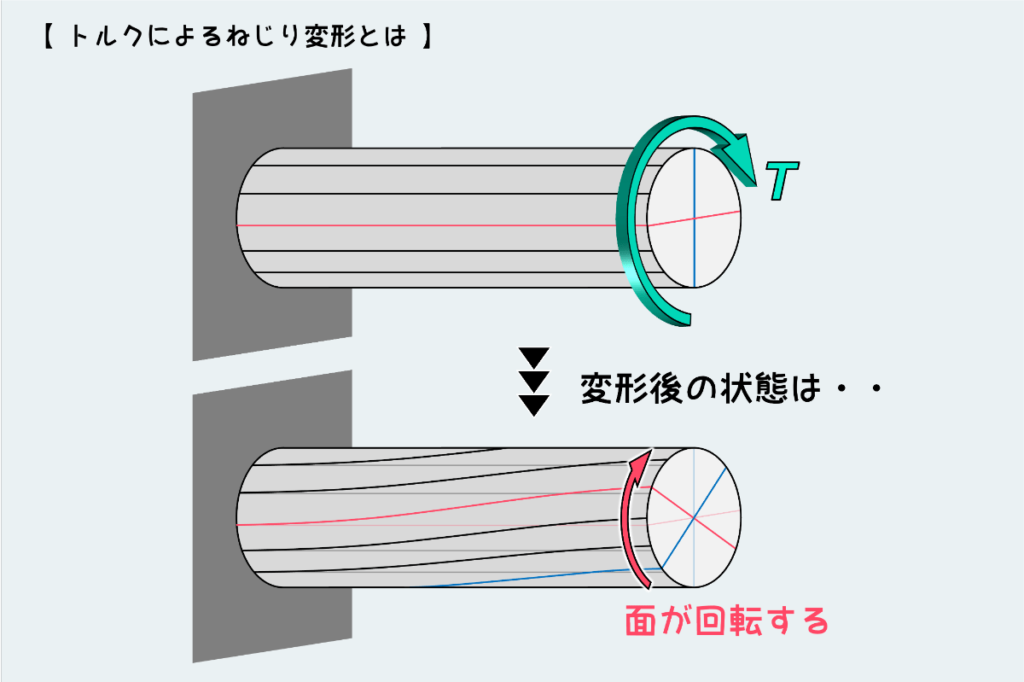
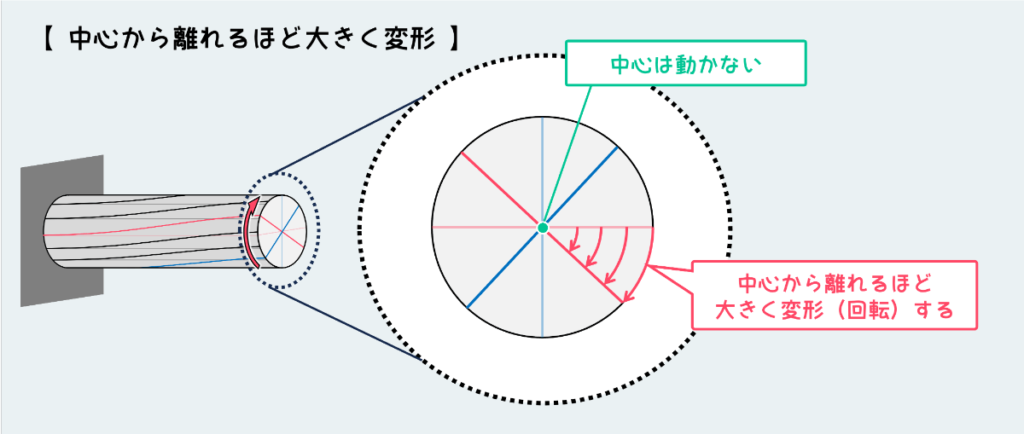
下図のように、この面の回転をよく見るといくつかの特徴がある。
まず、面の中心は動かない。さらに、中心から離れていくほど回転によって動く距離が大きくなる。
この動かない点を貫く軸のことを『中立軸』という。この棒の中立軸上の点は、どの断面においても動かない点だ。
ねじり変形は面の回転として現れる。中心（中立軸上の点）は動かず、中心から離れるほど大きく変形する。
さて、ここから応力状態の話に移りたい訳だが、以前別の記事でも書いた通りある面に働く応力状態を決めているのは『内力』だ。だから、まずはねじり問題において、内力がどういう風に伝わっていくかを把握することから始めよう。
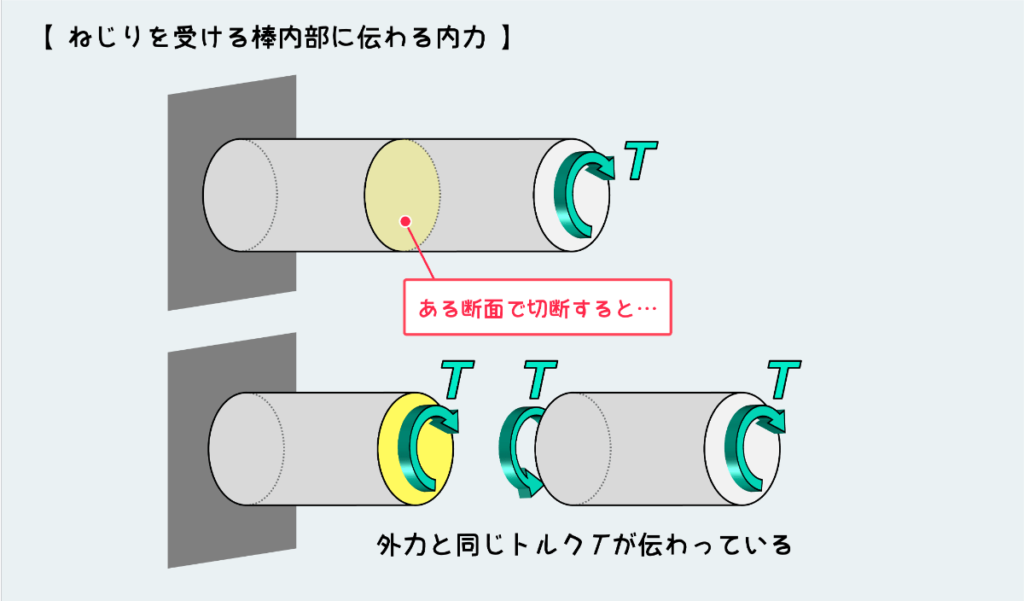
外力としてトルク T（ねじりモーメント）を受ける棒のある任意の面を仮想的に切断してみると下図のようになる。
自由体のつり合いと作用・反作用の法則からこの断面に働く内力を考えると、図の通り外力と同じトルク T が働くことになる。
これは切断する位置に関係ない話（切る位置が変わっても同じ結果になる）なので、トルク T を受ける棒には一定のトルク T が伝わっていくことになる。
すなわち、このようなトルクを受ける棒の横断面には、どの位置においてもこの後説明するせん断応力が分布しているということになる。
このことはねじり問題の特徴の一つなのでよく理解しておいてほしい。（ちなみに引張圧縮問題も同じ特徴を持っている。曲げの場合は少し事情が異なる）
外力としてトルク T（ねじりモーメント）を受ける棒の内部には、位置に関係なく外力と同じ大きさのトルク T が伝わっている。
では、内力としてあるトルク T が働く面にどのような応力が働くかを説明していきたい。
上で説明した通り、トルクを加えた棒の中心は動かず（変形せず）、中心から離れるほど大きく回転することになるが、この変形を実現しているのが『せん断応力』だ。
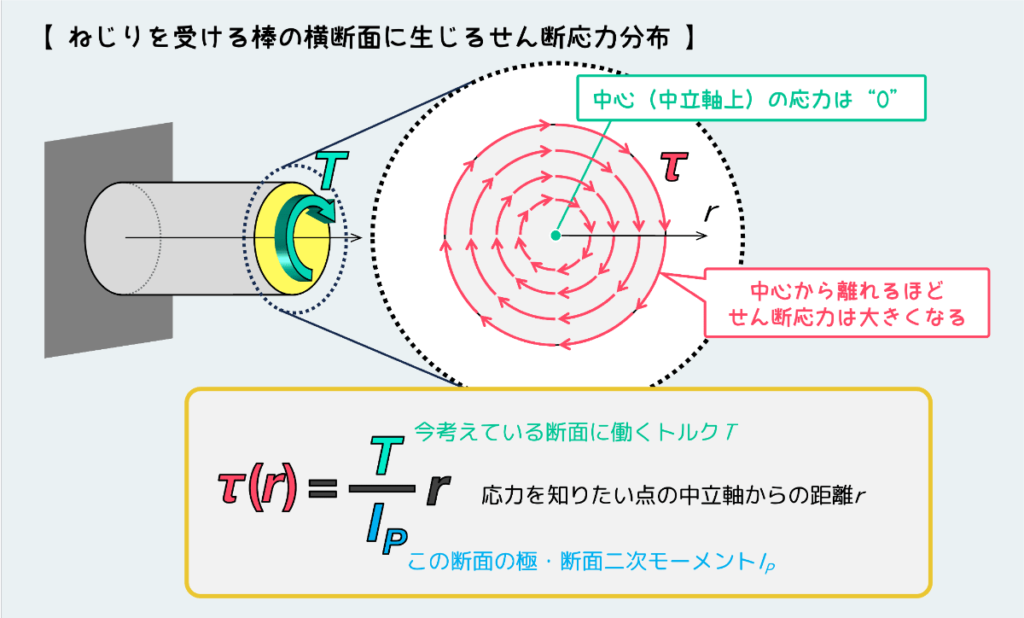
すなわち、トルクを受ける断面には下図のようなせん断応力分布が生じることになる。
中心のせん断応力は “0” で、このせん断応力が発生しない断面中心を貫く軸のことを「中立軸」という。また、中心から離れていくほどせん断応力は大きくなる。つまり、断面上の任意の点に働くせん断応力は中心からの距離 r に比例し、下図のような式で表される。
ここで分母にある IP は「極断面二次モーメント」と呼ばれるもので、断面形状に依存した量である。分子にあるトルク T は、今考えている断面に働くトルク T の大きさである。トルク T と極断面二次モーメント IP は状況が決まれば一定値に決まるものなので、このせん断応力は中立軸からの距離rに比例した形になっていることが理解できるだろう。
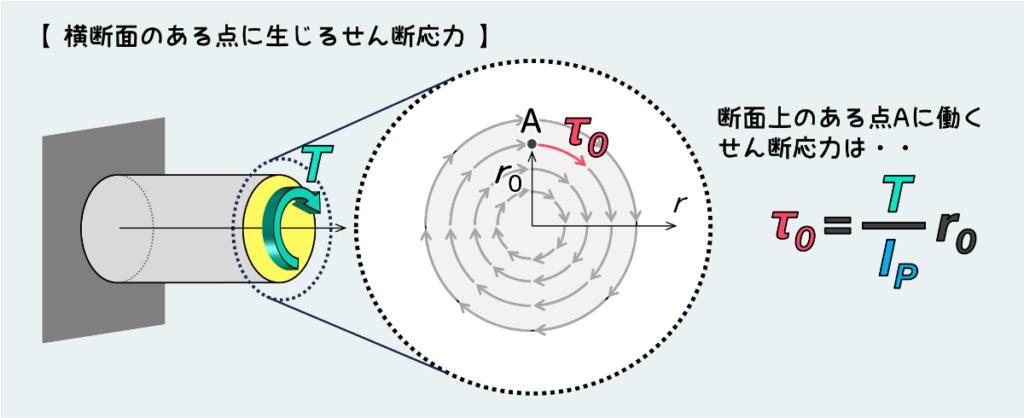
この式を利用することで、トルクを受ける棒内部の任意の位置に働くせん断応力を算出することができる。
たとえば中心から r0 だけ離れたA点（下図）に働くせん断応力 τ0 が知りたければ、下図のように公式の r のところに r0 を代入することで求めることができる。
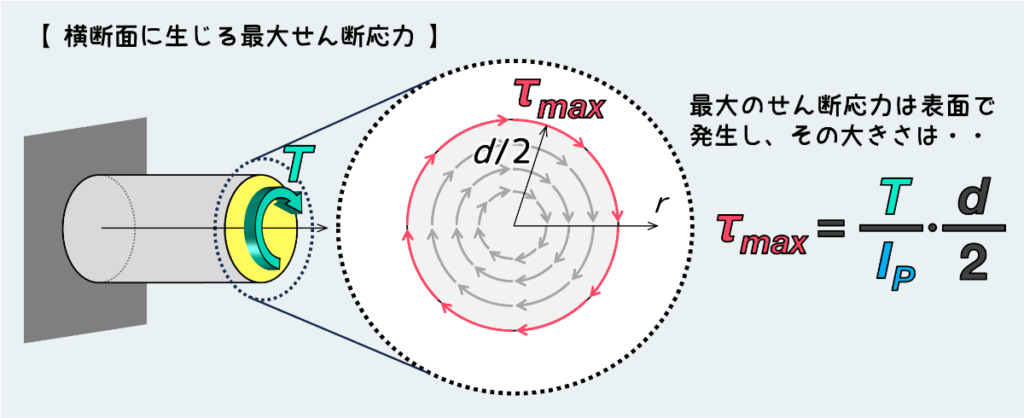
部材が安全かどうかを判断する上で重要なのは、やはり材料中に発生する最大の応力である。
上で示したせん断応力の式を見てわかる通り、応力が最大になるのは中心からの距離 r が最大になる位置、つまり部材表面である。
したがって、丸棒の場合は発生する最大せん断応力は、下図のように r = d/2（d：直径）を代入することで算出できる。
中立軸上の点の応力は “0”、中立軸から離れるほどせん断応力は大きくなる。最大せん断応力は部材表面で発生する。
ねじりを受ける丸棒とパイプに発生する最大せん断応力
上記の通り、ねじりを受ける部材に発生する応力の特徴およびその公式について説明した。
ここからは代表例として、丸棒およびパイプの場合に生じる最大せん断応力を紹介したい。
ねじり問題において、せん断応力を考えるために重要なのは『極断面二次モーメントIP』である。断面形状および寸法に応じて変わるこの極断面二次モーメントを正確に計算することが必要不可欠だ。
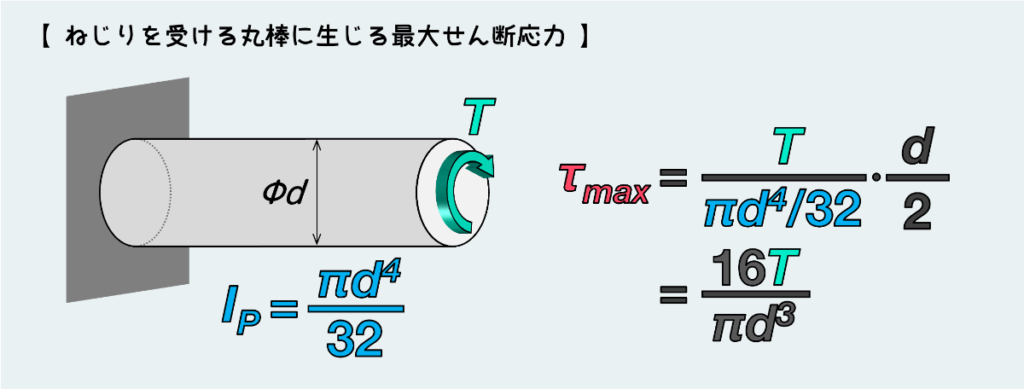
丸棒の場合は IP=πd4/32 なので（これは暗記しておいてもいいぐらいだ）、丸棒に発生する最大せん断応力は下図のように表すことができる。
ねじりを受ける部材の強度問題を考える際は、頻繁にこの最大せん断応力を考慮することになると思われるのでしっかり覚えておこう。
次にパイプ状の部材についてだ。
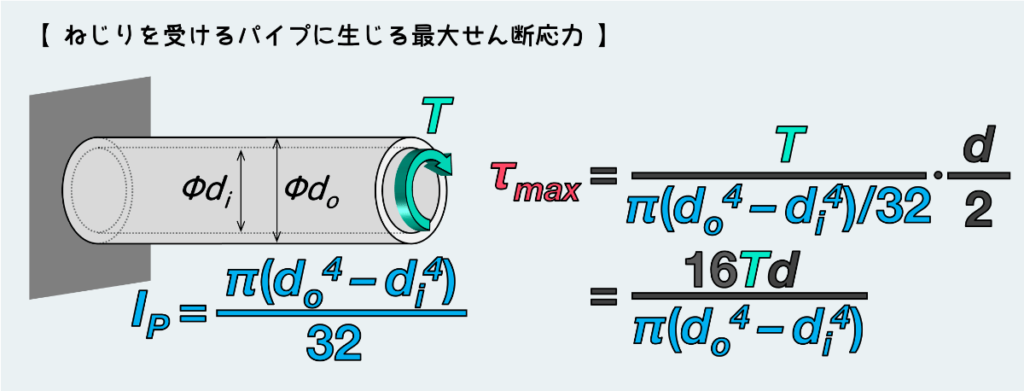
パイプの場合は断面形状はドーナツ状の形になるため、外側の大きな円の IP（πdo4/32）から内側の小さな円の IP（πdi4/32）を引くことで、このパイプの極断面二次モーメント IP が計算できるので、最大せん断応力は下図のとおり表せる。
丸棒にしてもパイプにしても最大せん断応力は表面で発生することを理解しておこう。
まとめ
トルク（ねじりモーメント）を受ける部材に生じるせん断応力について説明してきたが、理解できただろうか？
少しだけ引張圧縮問題とは違い、ややこしく感じるかもしれないが、起きている現象をよく理解していれば公式を使いこなすことは難しくないだろう。
次の記事ではねじりによる変形について解説したいと思うので、そちらの記事も合わせて読んでもらえると嬉しい。（執筆中）
- ねじり（トルク）を受ける材料の横断面には、位置に関係なく外力と同じ大きさのトルクが伝わっている。
- ねじりを受ける部材の横断面にはせん断応力が発生し、中立軸上では応力“0”で、中立軸から遠ざかるほど（半径rに比例して）せん断応力は大きくなる。
- せん断応力を求めるには極断面二次モーメントが必要。
