前回までの記事でSFD・BMDの考え方から描き方、特徴を一通り説明してきた。
今回の記事では、６つの色んな具体例を通して、描き方とSFD・BMDに現れる特徴を解説したい。これを見れば、SFD・BMDの描き方をより深く理解・実感できると思う。
これまでのSFD・BMDに関する記事は以下の通り。
材料力学 SFD/BMDって何？その意義を超詳しく解説【材力Vol. 6-1】
材料力学 絶対描けるようになるSFD/BMDの描き方を徹底解説【材力Vol. 6-2】
材料力学 SFD・BMDの押さえておきたい大事な特徴と４つの特定パターン【材力Vol. 6-3】
- とにかく手順に従っていけば、どんな問題でもSFD・BMDを正しく描ける。
- SFD・BMDに現れる特徴を理解し、ちゃんとそれが反映されたグラフになってるか注意する。
- 材質や断面形状の変化はSFD・BMDを描くだけなら気にする必要なし。
※この記事全体は長いので、下の画像と目次を見て、気になる所だけを見てもらえばと思う。
夢へ駆ける少女の姿に感涙！！
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか？」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい！」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanなら2/4までなんと3巻無料で読めてしまいます！まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです！
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
SFD・BMD描き方の手順をおさらい
まずは手順をおさらいしよう。
はり全体を支点等から切り離して、自由体として取り出し、平衡条件から反力を求める。片持ちばりの場合はこのステップはスキップして良い。
はりを左から眺めていき、何か状況が変化するポイントでは場合分けが必要。
切断した断面には、正の向きにせん断力と曲げモーメントを仮置きする。はりの左端から切断した所までの距離をxとおく。
切断した位置をxとして平衡条件を考える。FとMは切断した位置xの関数として求まる。STEP.2で場合分けしたときは、場合分けの数だけ、STEP.3とSTEP.4を繰り返す。
横軸x、縦軸Fもしくは縦軸Mのグラフを描く。節目のポイントでは、xに具体的な数値（もしくは文字）を代入して、その位置でのFおよびMを求め、グラフに描き込むと良い。
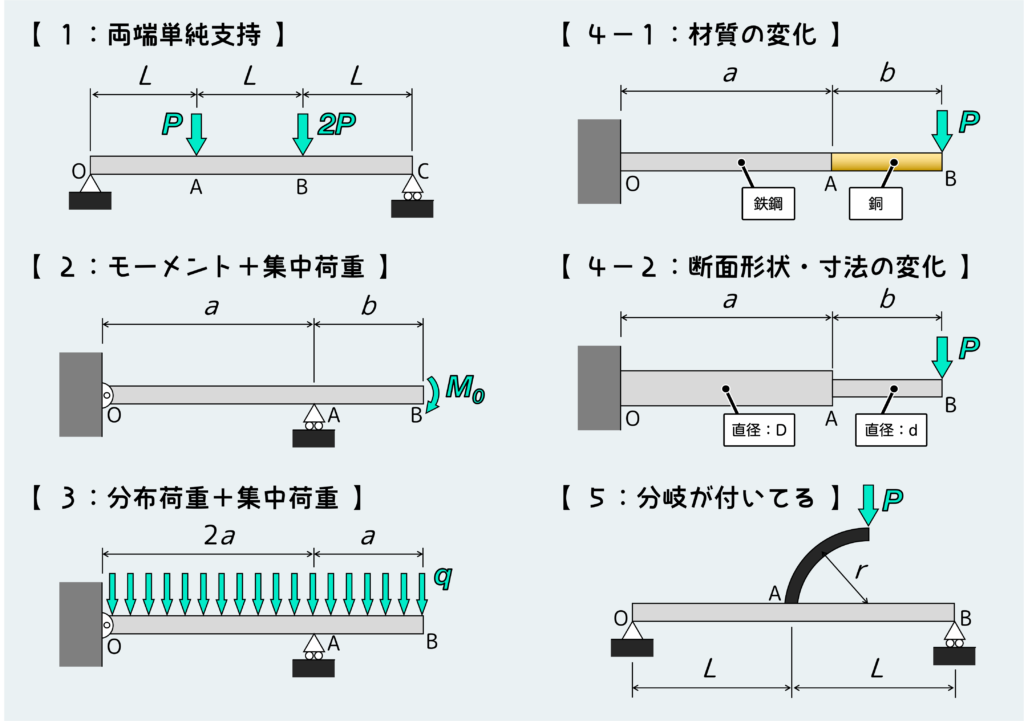
両端単純支持のはり
まずは両端を単純支持（回転支持）したはりの問題を考えよう。
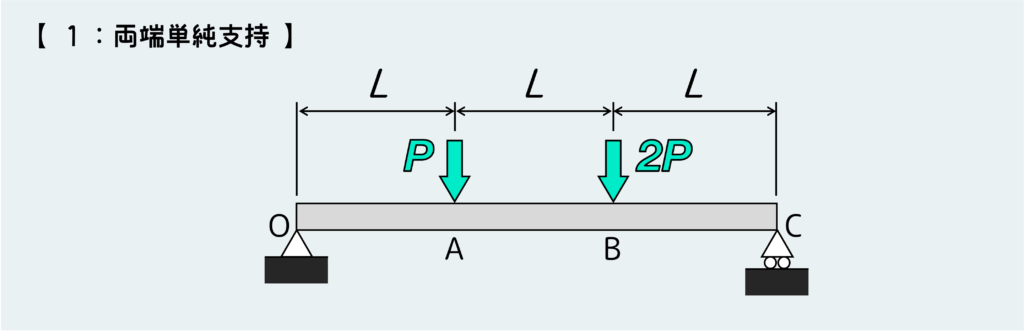
まずは手順に従ってO点およびC点の反力を求める。反力を求めるためには、はり全体を自由体として取り出して（支点から切り離して）つり合いを考えればよい。
ここでのポイントは、支持方法によって発生する反力の種類が変わるということだ。なので、支持方法をしっかり確認して、そこに発生する可能性のある反力だけを自由体図に描き込むことが重要だ。
支持方法と反力の種類については、下の記事を読んでみてほしい。
材料力学《全員必見・超重要》自由体の考え方（色んな支持方法）【Vol. 1.2-2】
この問題ではO点もC点もナイフエッジなので、上下方向の反力だけが発生する。これを元につり合いを考えると下のようになる。
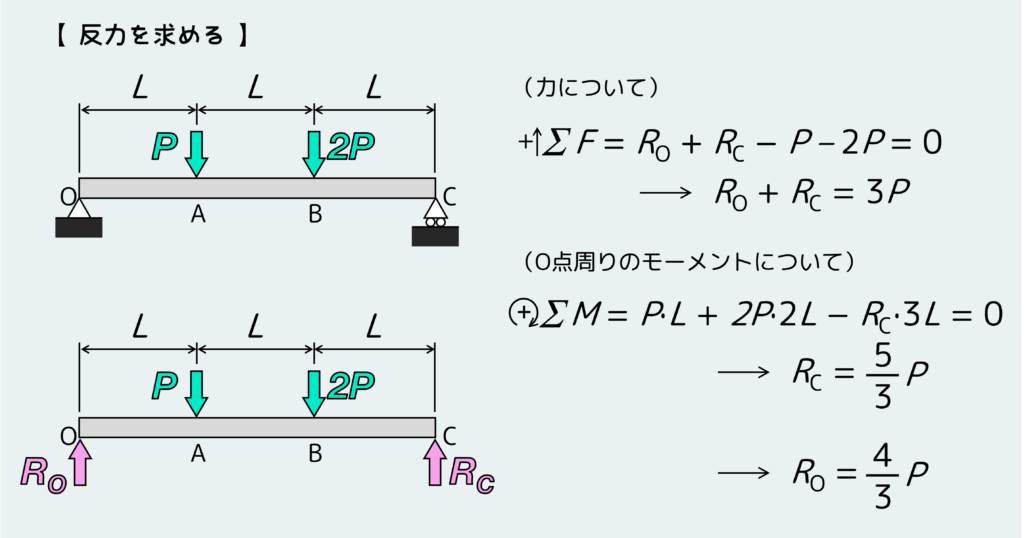
次に場合分けの必要性を確認しよう。場合分けが必要なポイントは状況が変化する場所だ。今回はA点とB点で外力が加わっているので、この２箇所を境にして場合分けする。
つまり、OA間、AB間、BC間の３つについて、そこに伝わるせん断力Fと曲げモーメントMを考えていく。
まずはOA間、つまり 0 < x < L のとき。ポイントは計算が簡単そうな自由体の方で平衡条件を考えることだ。
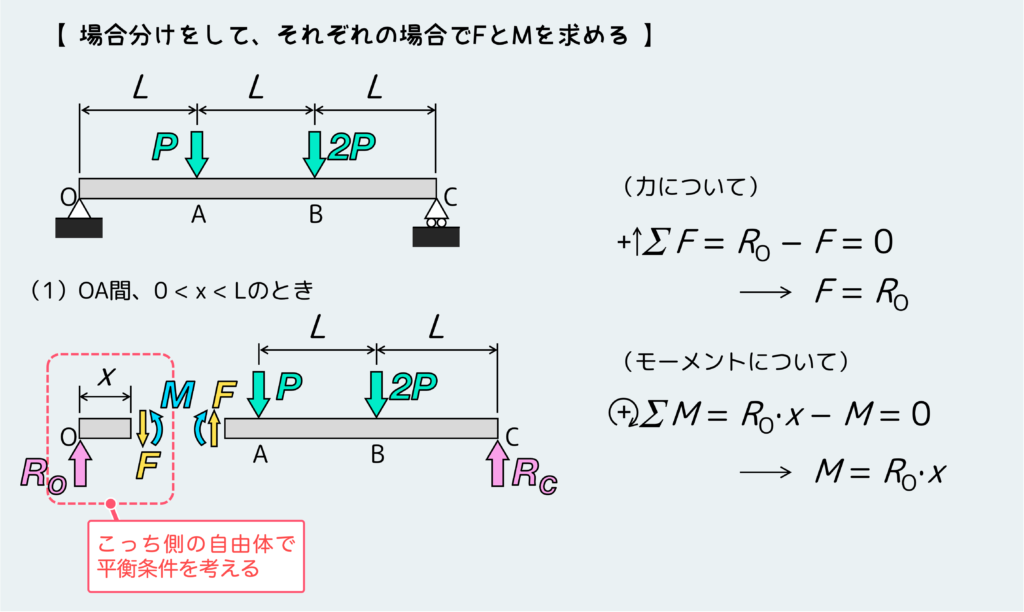
次はAB間、つまりL < x < 2L のとき。
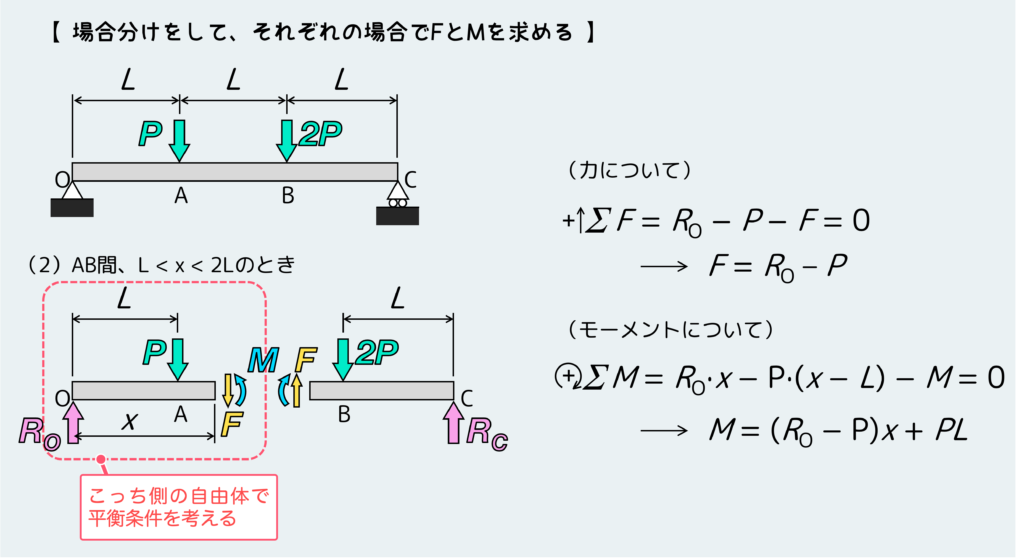
最後にBC間、つまり 2L < x < 3L のとき。
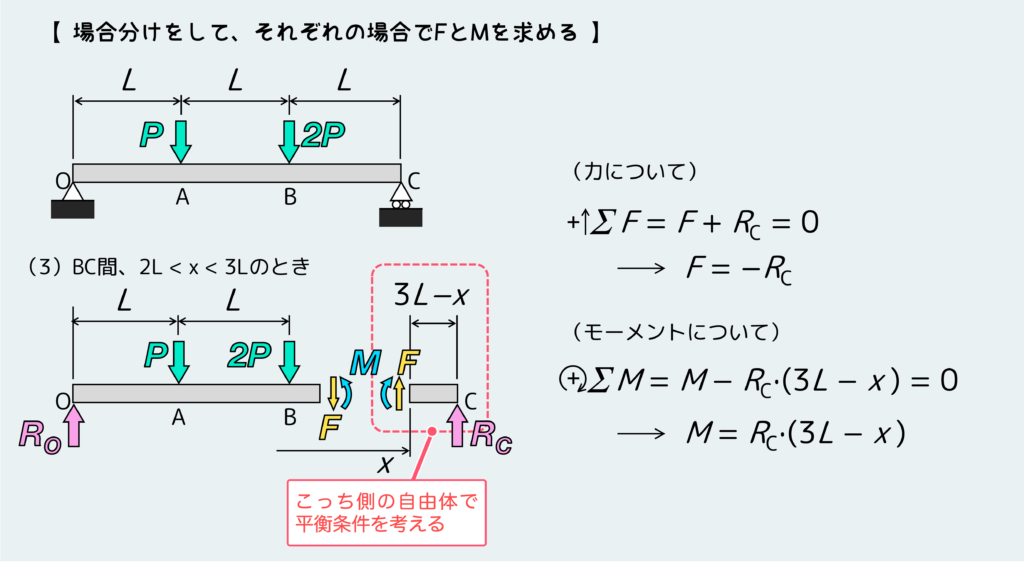
ここまで来たら、全部を整理して、SFD・BMDをグラフに描こう。グラフを描くときはなるべき正確に描こう。そうすることで、くだらない間違い・ミスを防ぐことにつながる。
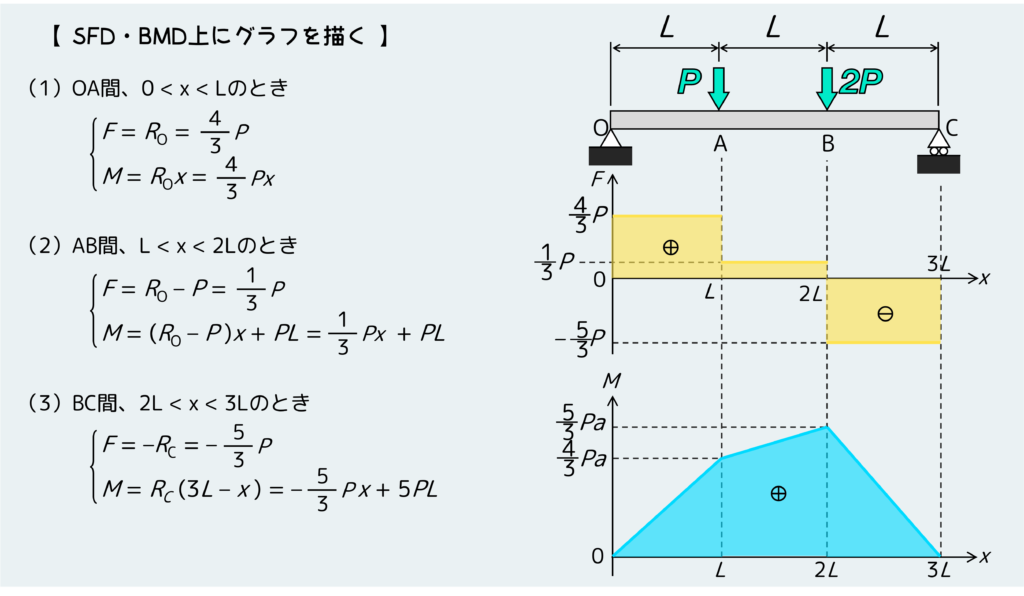
こんな感じでSFD・BMDを描ければ、このはりではB点が最も危険な位置で、この位置の曲げ応力を計算するのに必要な曲げモーメントの大きさは”5P/3″だということが分かる。（はりの断面が一様だと仮定した場合）
さて、前の記事で説明したような特徴がちゃんとSFD・BMD上に現れてるのか最後に確認してみよう。
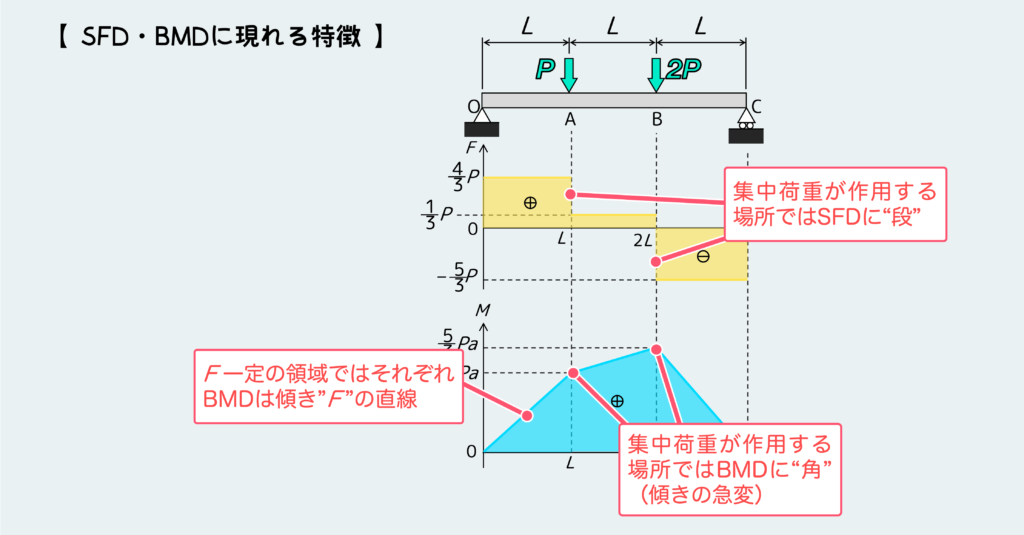
モーメント＋集中荷重
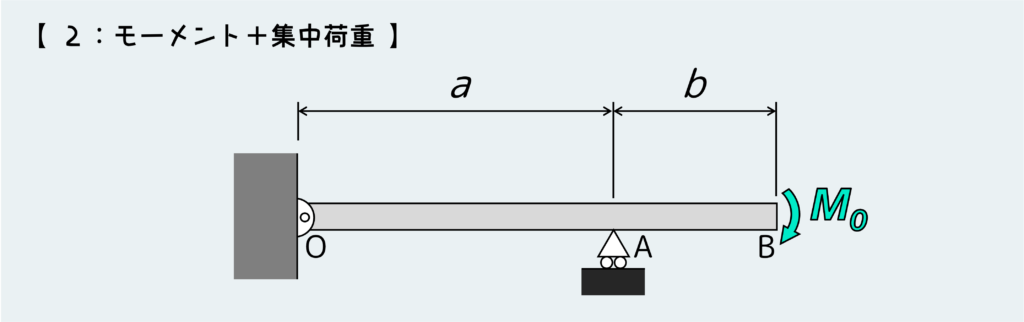
では次はモーメントが作用するこんな問題を考えよう。
ところで、モーメントだけが作用するってどういう状況ですか？みたいな疑問を持つ人に出会うことがある。もっともな疑問だと思う。
たしかに集中荷重はすんなりイメージできるけど、モーメントだけってなんだかイメージしにくい。荷重をかけずにモーメントだけをかけることなんてできるのだろうか？
モーメントだけが働くような状況のからくりは実は下の絵のようなものだ。
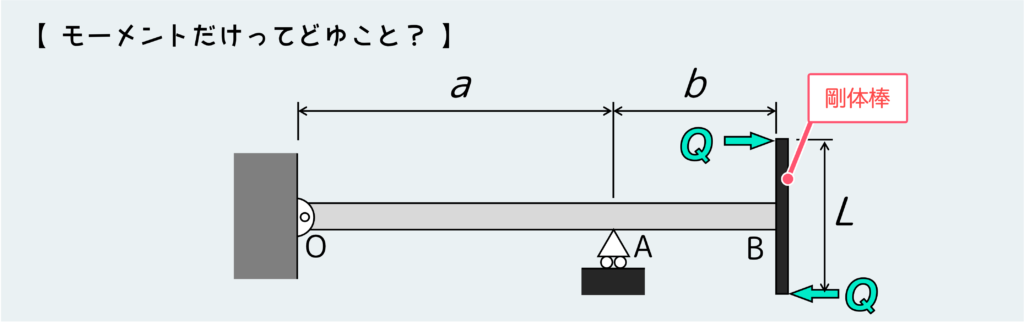
モーメントってのは必ず偶力という力のペア（同じ大きさで反対向きの２つの力）によって生み出される。
なのでこの絵のような２つの力Qのペアによってモーメントが発生する。
はりの先端に取り付けた剛体棒だけ切り離すと、下のように内力が伝わってることが分かる。ここで仮にM0=QLだとすれば、最初の問題図のように、先端にモーメントが作用したはりになる訳だ。
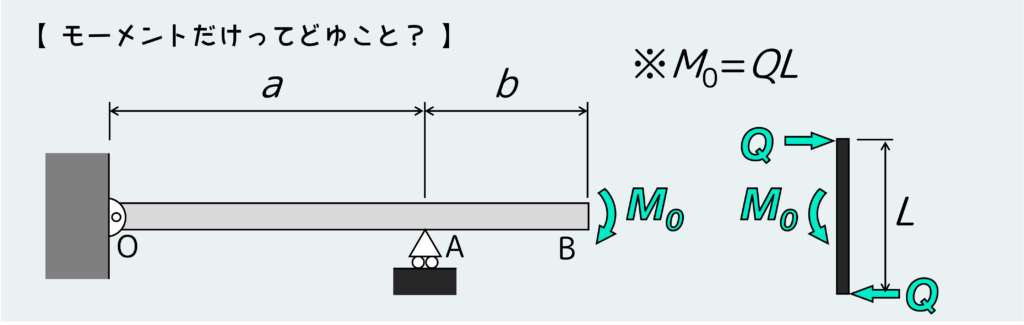
なので、実際には荷重が存在しない状況下でモーメントだけが単独で存在することはない。どこかにそれの元となっている偶力があるはずだ。でも問題でいちいちそこまで書いてると図が煩雑になっていくので、省いてるということだ。
はい、では気を取り直してSFD・BMDを考えよう。まずは反力を求めると下のようになる。繰り返しになるが、ポイントは支持方法によって発生しうる反力の種類が限定されることだ。
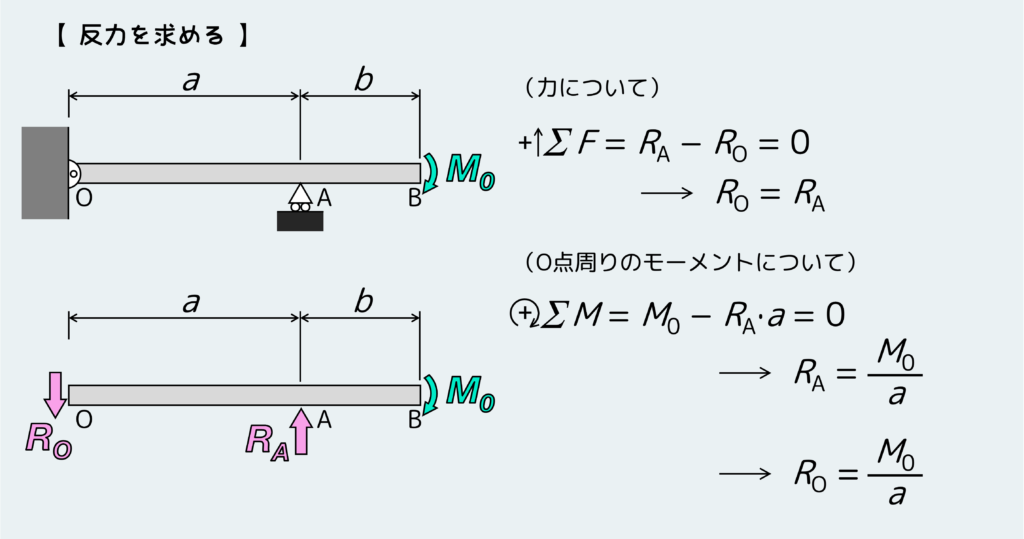
次に場合分けをして、それぞれの場合で平衡条件を考える。今回はA点に支点があり、ここに反力が加わるのでOA間とAB間の２パターンに場合分けする。まずはOA間。
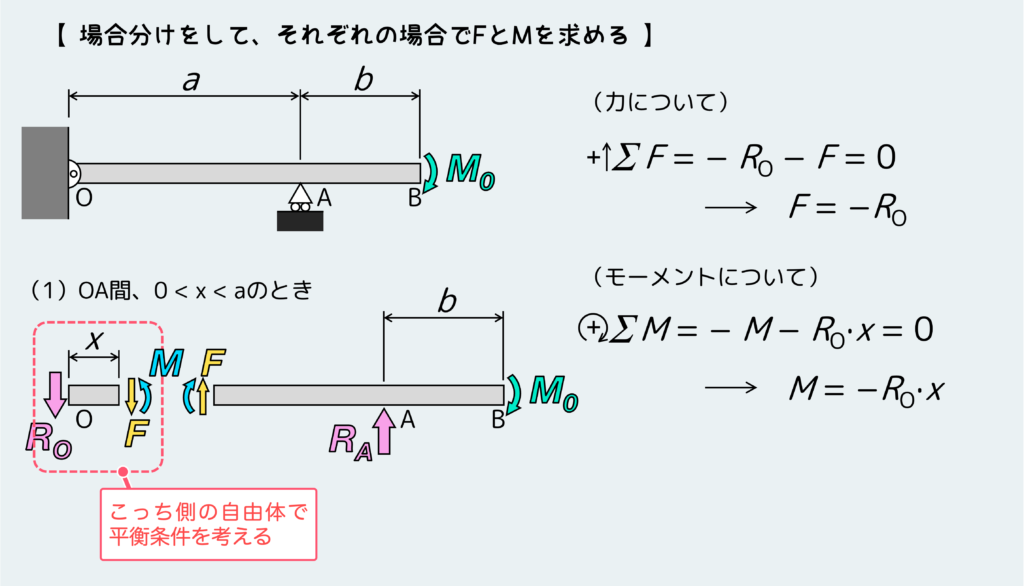
で、次にAB間。
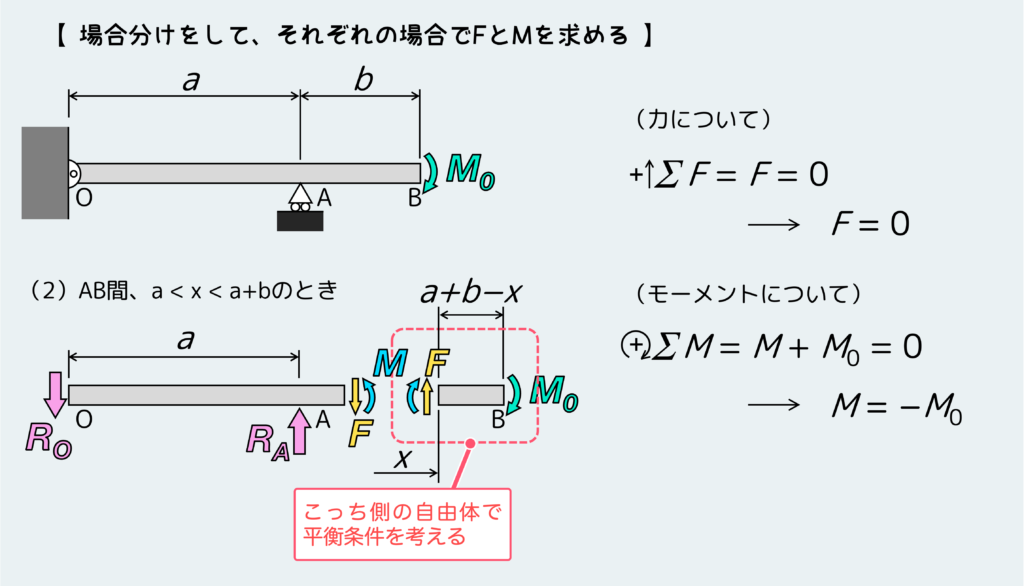
求めたFとMを元にグラフ化すると、下のようになる。
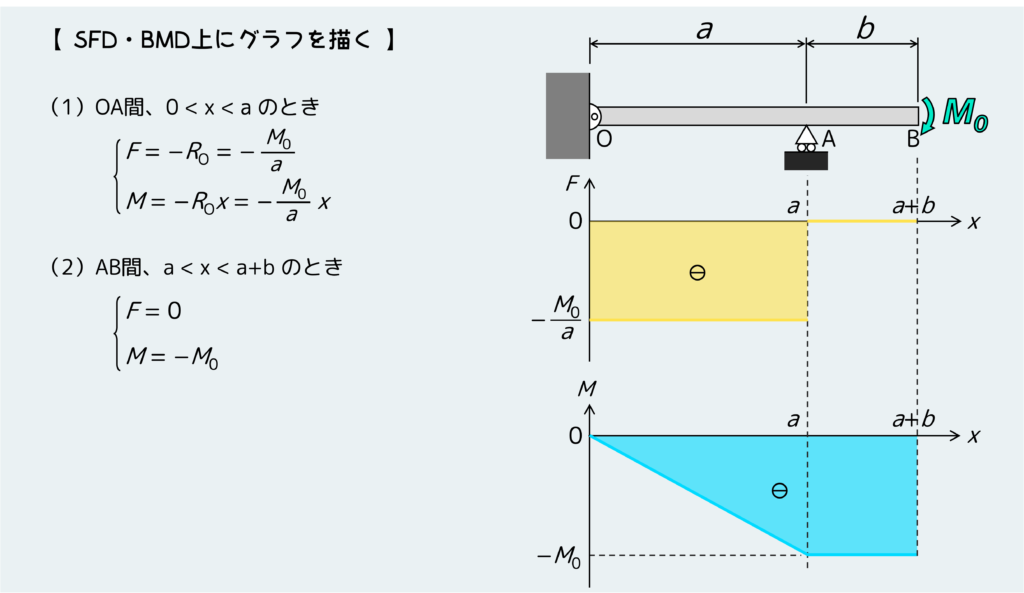
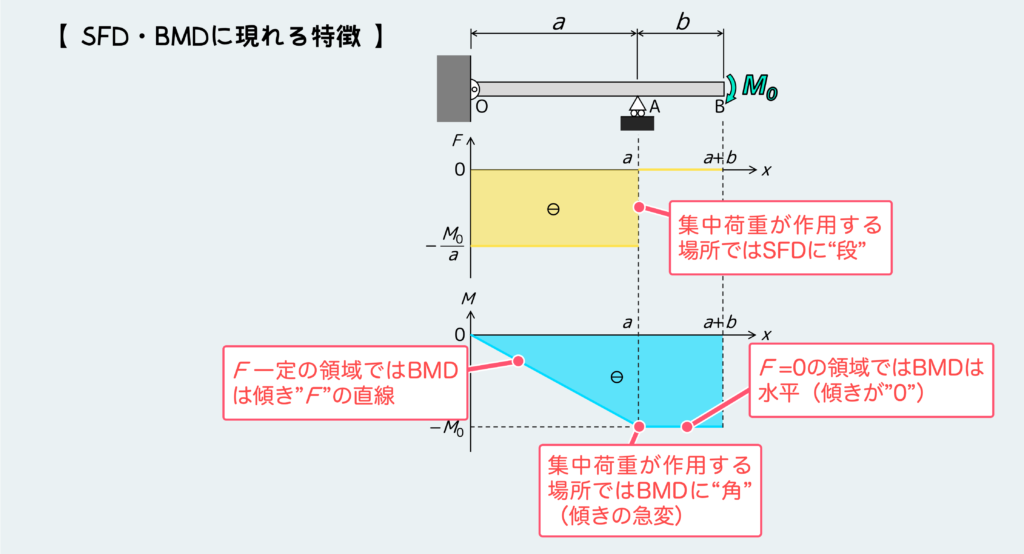
今回のSFD・BMDから見て取れる特徴は下のような感じだ。
分布荷重＋集中荷重
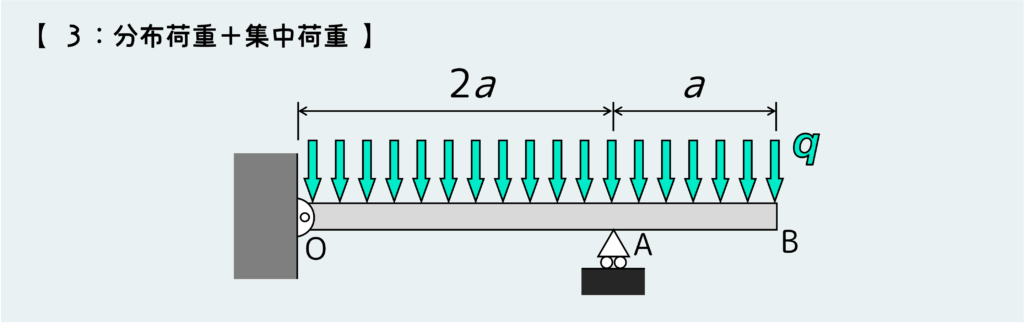
さあでは、上のような分布荷重の問題も考えてみよう。
まずは例によって反力を決定しておこう。毎回言ってるけど、支持方法によって発生する反力の種類が変わることに注意しよう。
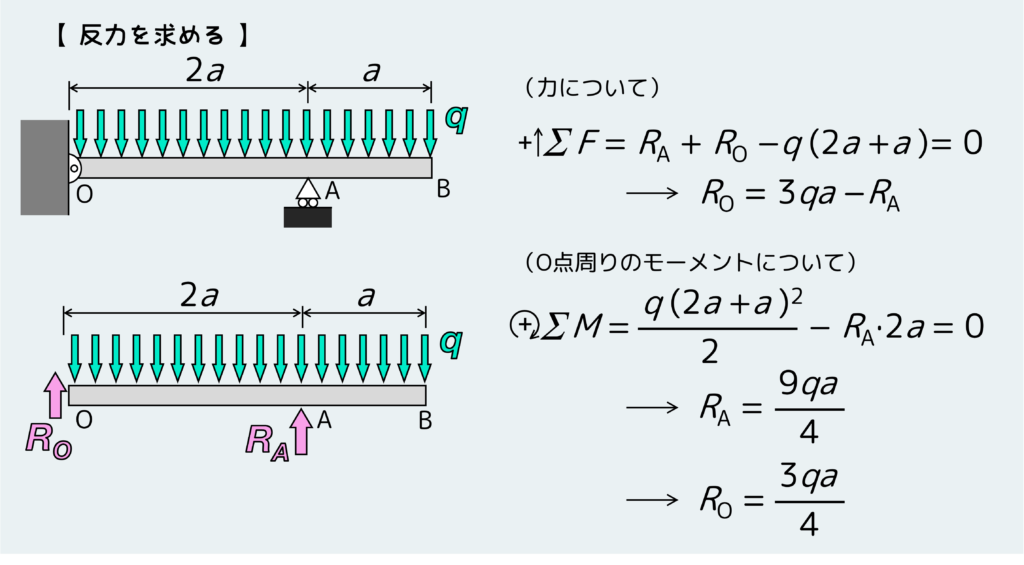
反力が求まったら、場合分けをしてそれぞれの場合で平衡条件から内力FとMを求める。
分布荷重の問題では、平衡条件式を立てるときには分布荷重を集中荷重に置き換えて考えるのがポイントだ。
下の絵のような自由体の平衡条件式を立てるときは、集中荷重”qx”が自由体の中央（左右端から”x/2″の位置）に働いているものとみなして式を立てるってことだ。
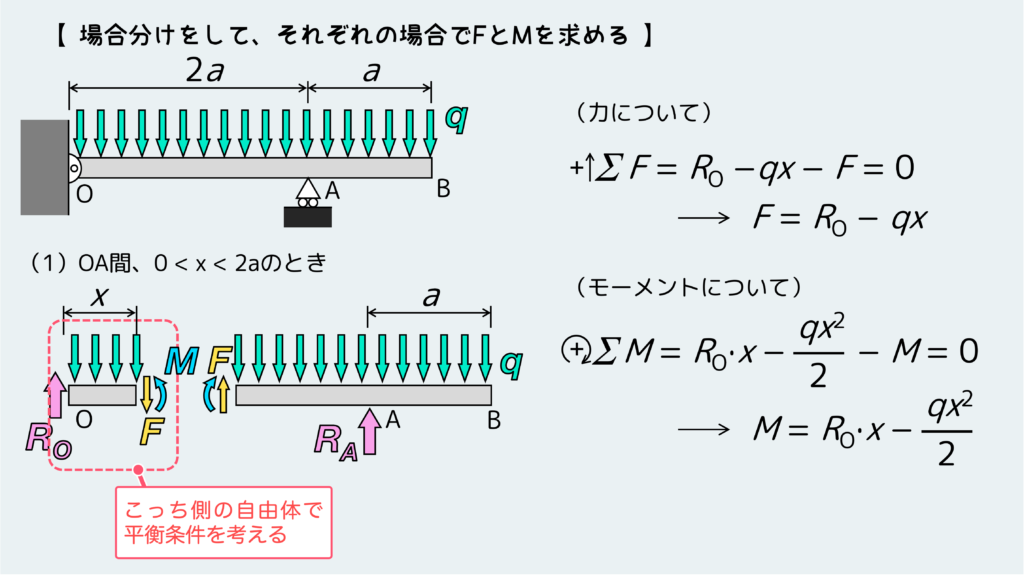
場合分けのパターン２（AB間）についても同様にFとMを求めよう。
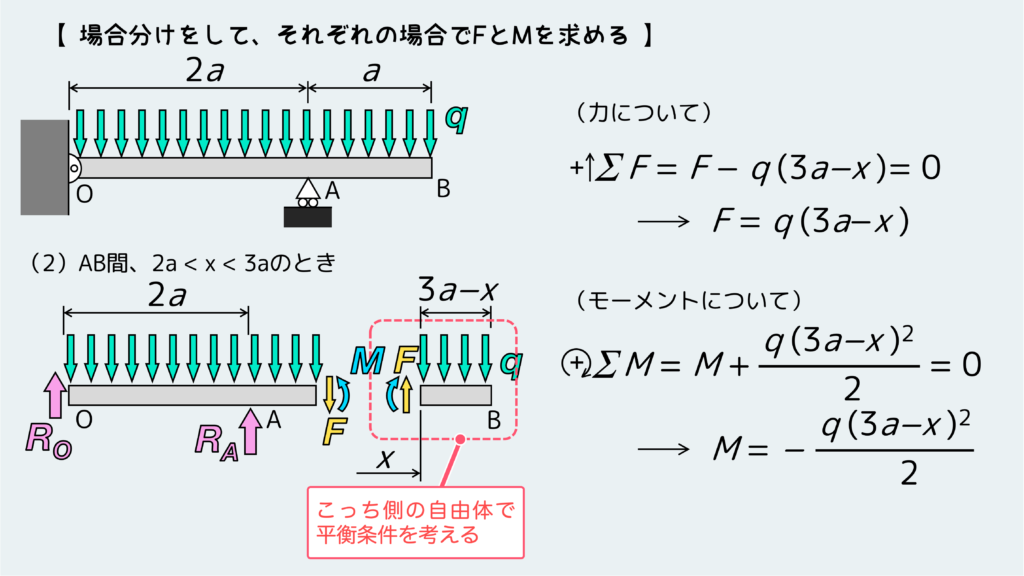
分布荷重の問題では、Fの式がxの一次関数となり、Mの式がxの二次関数となるので、他の問題と比べてわりと式が複雑になる。なので、計算ミスをしないように注意しよう。求めたFとMをグラフに描くと下のようになる。
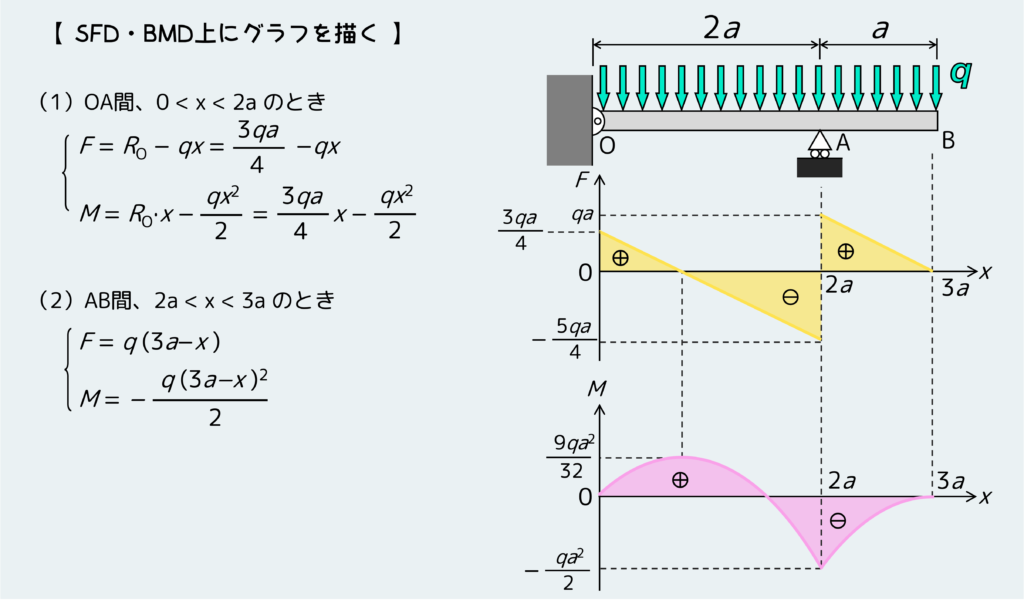
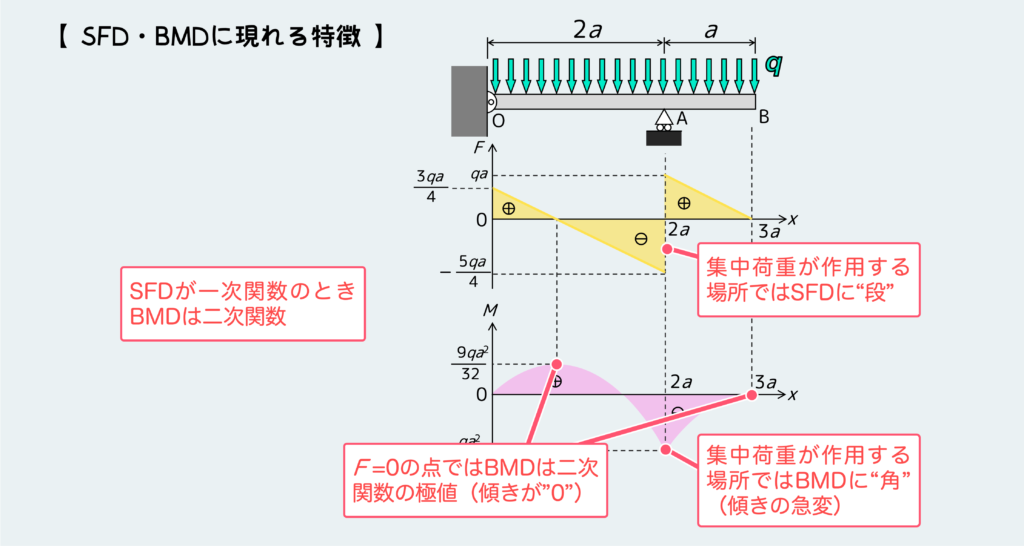
分布荷重の問題ではMの式が二次関数になるので、図のように放物線を描くことになる。このとき適当に二次関数のグラフを描かないように気を付けよう。
つまり、BMDの傾きが同じ位置のFの値になるという特徴がちゃんと反映されたグラフになるように描こうということだ。分かりやすいところでは、F=0になる位置では、BMDの傾き（二次関数の接線の傾き）が”0″にならないといけないので、グラフは極値をとることになる。こういうことに注意しながらグラフを描こう。
材質や断面形状・寸法が変化するはり
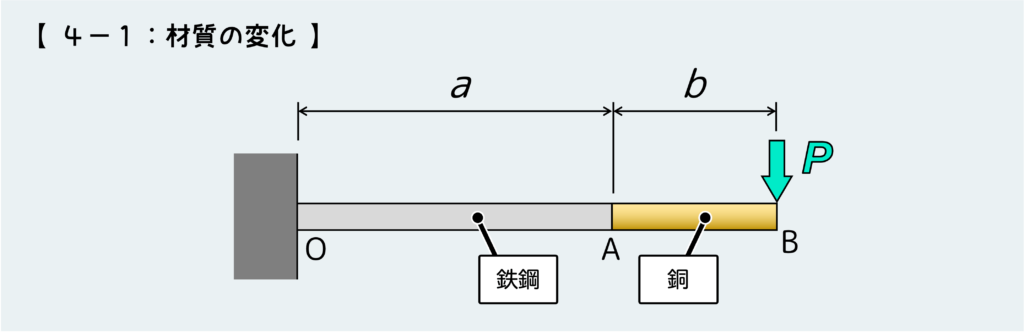
時にこんな問題を考えることもあるかもしれない。はりの途中で材質が変化するような場合だ。
なんだか複雑になる気がするだろうか？どうだろう？
答えは次の断面形状・寸法の変化と合わせて説明しよう。
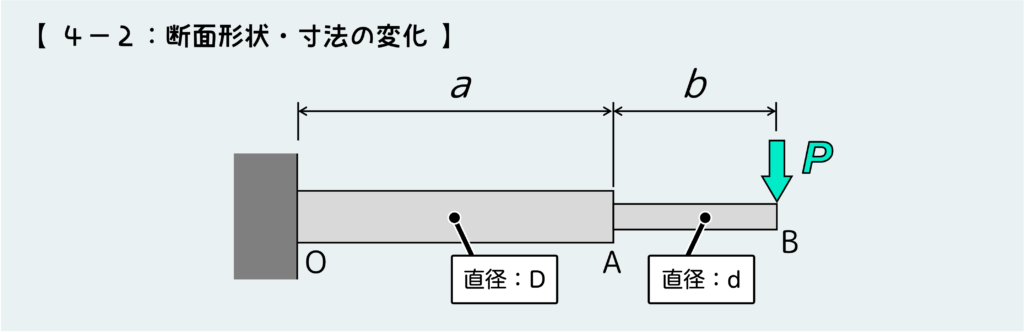
断面形状や寸法が変化するような問題も考えられる。こんな場合はどうなるだろうか？
上の２つのような問題は、はっきり言って恐るるに足らず。要はひっかけ問題だ。
結論を言うと、SFD・BMDを考える上では材質の変化や断面形状の変化は全く気にする必要はない。なぜならSFDやBMDは材料中を伝わっていく内力を相手にしたものだからだ。
材質がどうなろうと、断面形状がどう変化しようと、そこに伝わる内力は変わらない。材質が影響するのは変形や破壊に関することで、断面形状が影響するのは応力だ（応力が影響されるから変形や破壊にも影響する）。
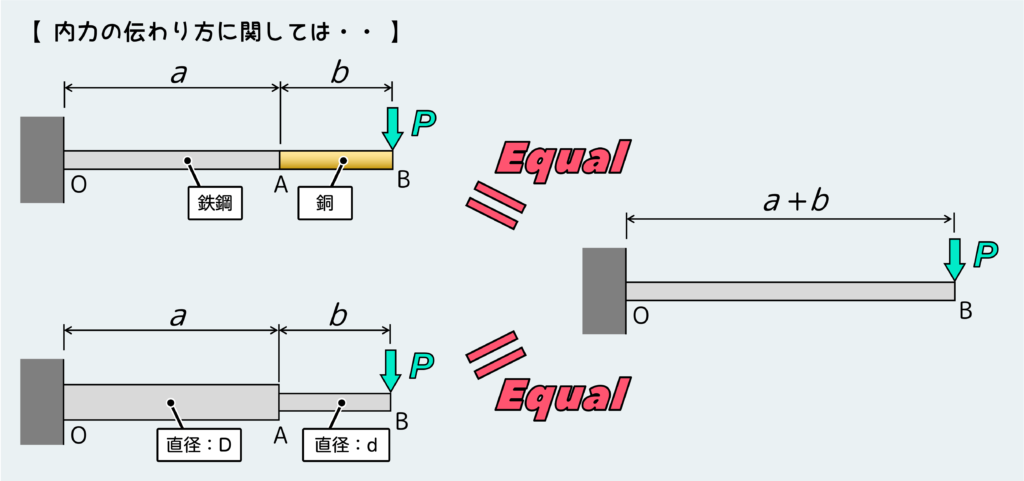
すなわち、SFD・BMDを考えるだけなら、上のような問題は長さ”a+b”の肩持ちばりが先端に荷重”P”を受ける問題と同じとみなせる。
材質や断面形状の変化は気にせず、問題を解けばよい。
途中で分岐があるはり
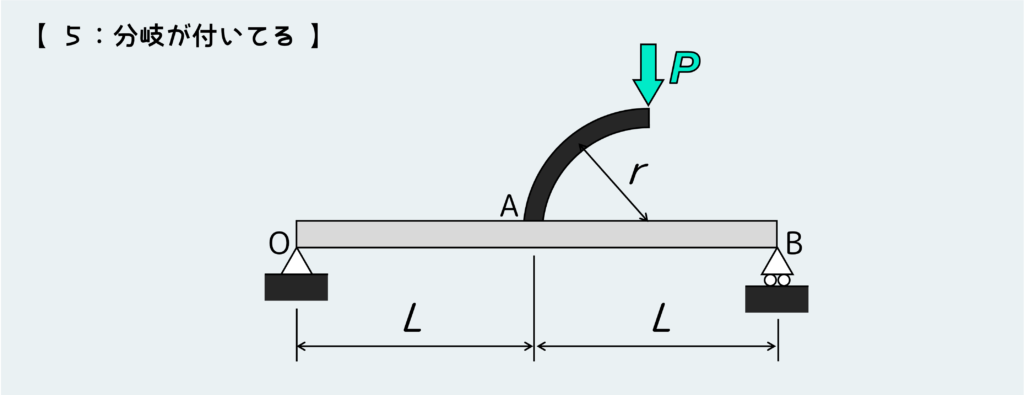
最後に、はりに分岐が付いたような問題を考えよう。上の問題では、はりの中央A点において分岐があり、その先端に荷重Pが作用している。今この分岐は剛体であり（いや別に剛体じゃなくても良いんだけど）、あくまでSFD・BMDを考えるのははりOBとする。
この問題のアプローチは１つじゃないが、個人的にはあんまり分岐があることを気にせず解いていくやり方が良いように思う。
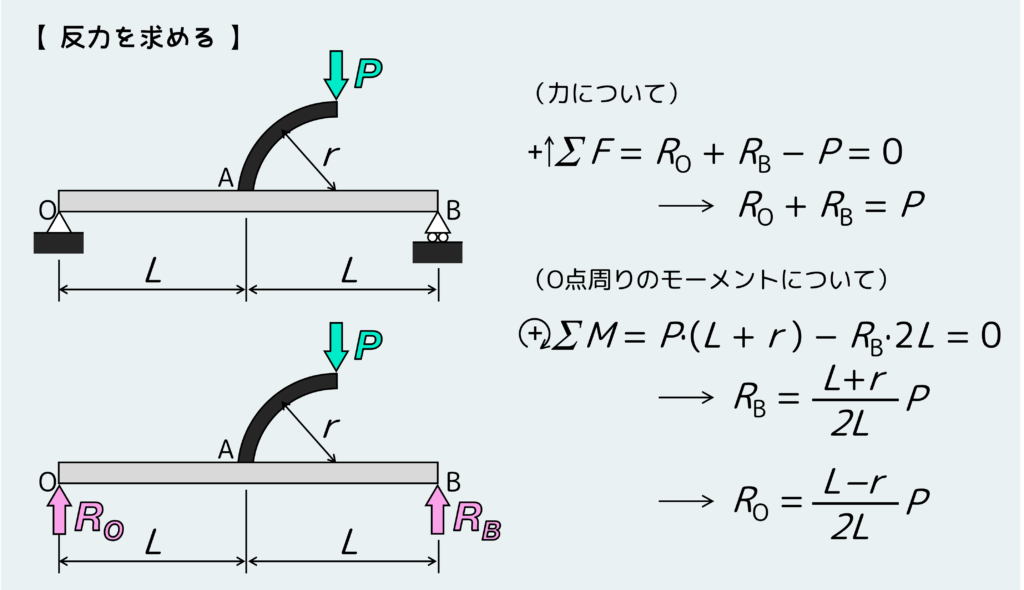
という訳で、いつもの手順にしたがって進めよう。まず反力を求める。
反力は、いつものように支点から切り離したはり全体（分岐含む）を自由体として取り出して、平衡条件から求める。
次に場合分けをして、それぞれの場合について内力FとMを平衡条件から求める。分岐がある問題では、分岐がある位置を境にして場合分けを行う。
まずは分岐手前のOA間について。
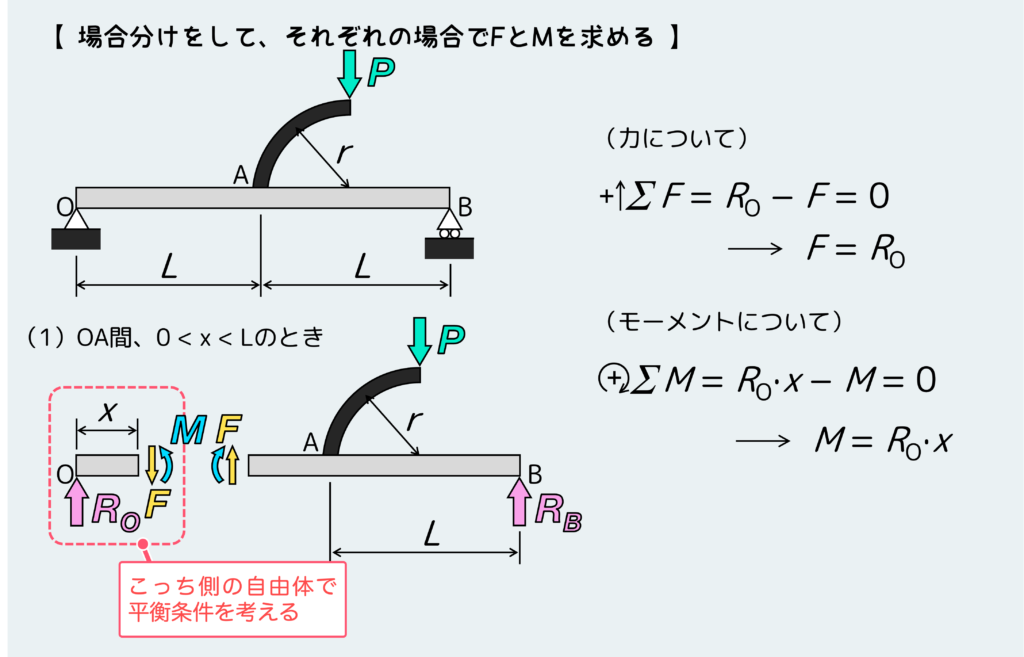
次に分岐より右側のAB間について。どちらの場合も、分岐を含まない方の自由体で平衡条件式を考える方が楽だと思う。
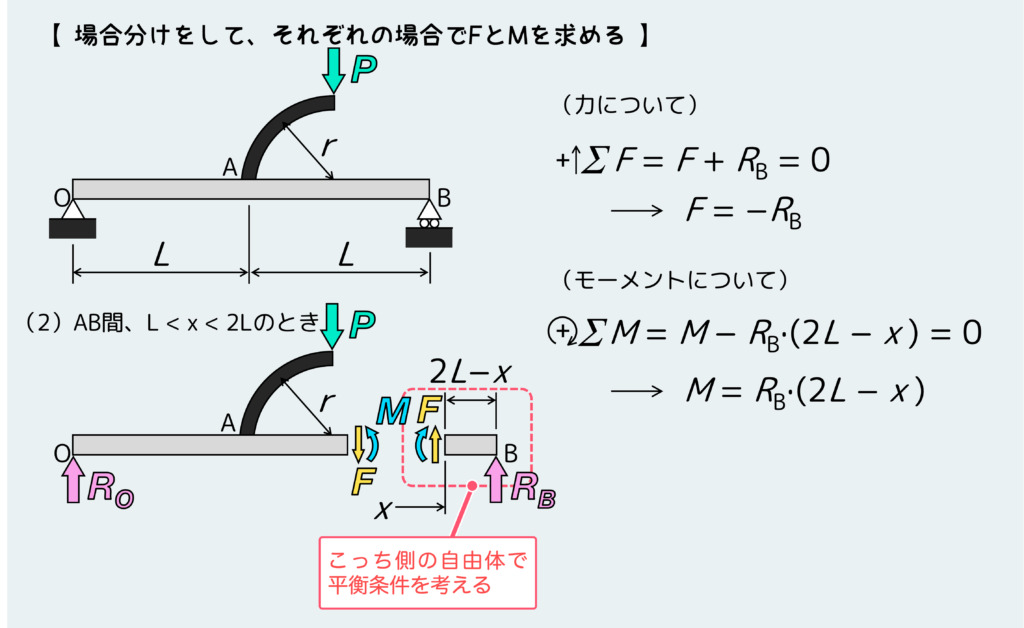
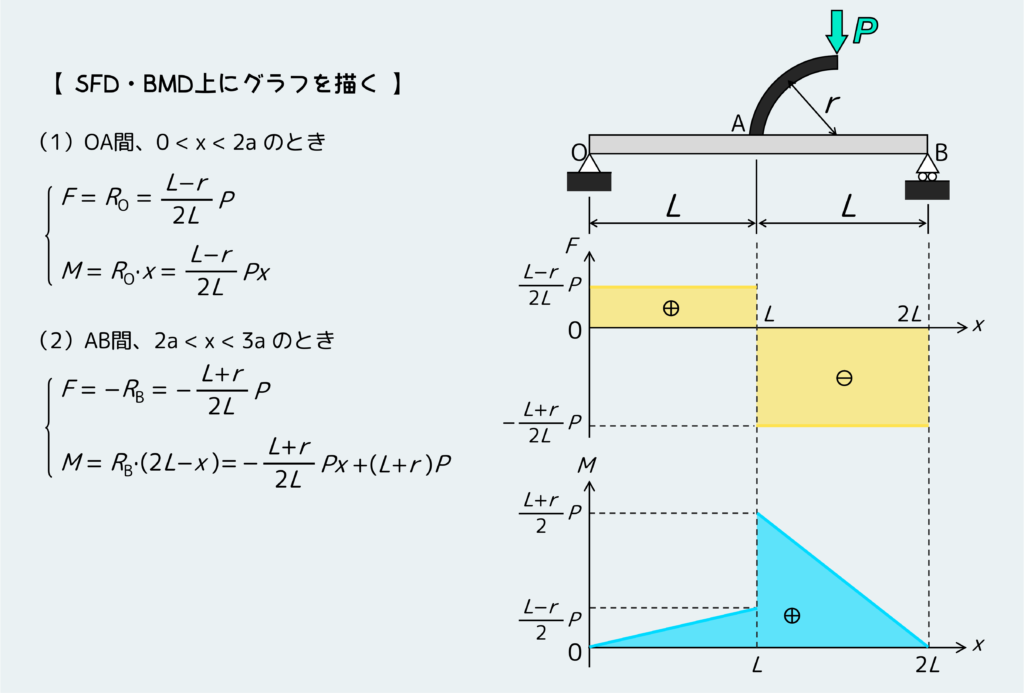
それぞれの場合で、FとMを求めたらグラフにSFD・BMDを描こう。下のようになる。
分岐が付いている割に思ったほど複雑にならないな、と思った人も多いのではないだろうか。ていうか、場合分け２パターンともに分岐を含まない自由体に対して平衡条件を考えており、このやり方でちゃんと分岐のことを考えたことになるのか？と疑問を持つ人もいるかもしれない。
しかし、そんな心配は無用だ。なぜなら、最初の反力R0、RBを求めるときに分岐の影響を受けているからだ。なので、分岐の影響はちゃんと反力R0、RBの中に含まれているのである。
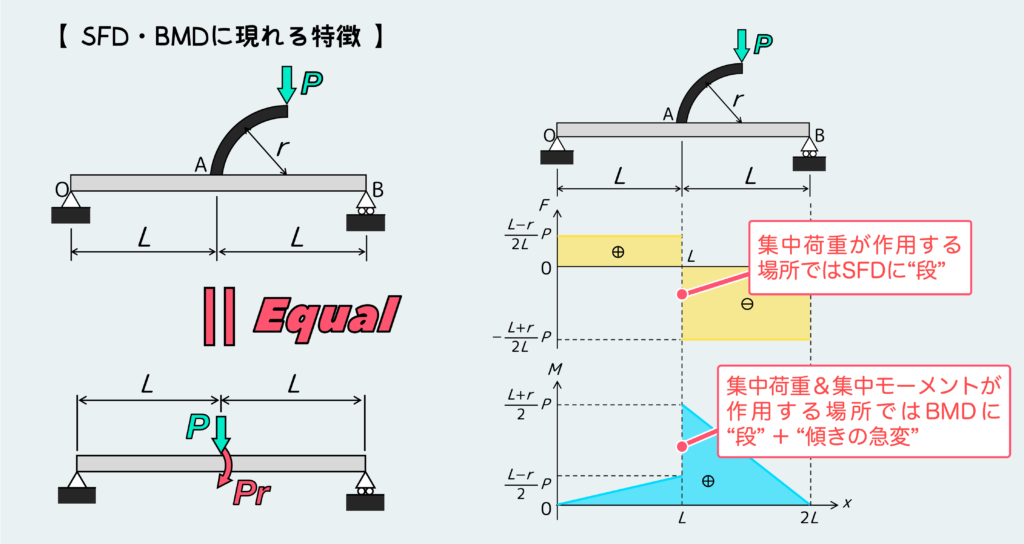
最後にSFD・BMDに現れる特徴について確認しよう。
こういう問題は、下の絵に描いたように分岐の根本に集中荷重とモーメントが働くような問題と等価なので、その特徴が反映されたようなSFD・BMDになる。
まとめ
具体例６個を通してSFD・BMDについて詳しく見てきたが、どうだろうか？
この中の一つでもみなさんの役に立つものがあれば嬉しく思う。
ここまで４回の記事でSFD・BMDについて詳しく見てきたが、曲げ問題においてSFD・BMDはとっても大事なものだ。これがまず分からないと応力や変形、破壊といった問題に入っていけない。
SFD・BMDについて自信が持てない人は、もう一度今回を含めた全４つの記事をよく見返してみてほしい。
材料力学 SFD/BMDって何？その意義を超詳しく解説【材力Vol. 6-1】
材料力学 絶対描けるようになるSFD/BMDの描き方を徹底解説【材力Vol. 6-2】
材料力学 SFD・BMDの押さえておきたい大事な特徴と４つの特定パターン【材力Vol. 6-3】
次の記事では、曲げによる応力について解説したいと思う。
- とにかく手順に従っていけば、どんな問題でもSFD・BMDを正しく描ける。
- SFD・BMDに現れる特徴を理解し、ちゃんとそれが反映されたグラフになってるか注意する。
- 材質や断面形状の変化はSFD・BMDを描くだけなら気にする必要なし。
研究者を志す者 必読！！
全8巻完結
こんなにも知的探究心を刺激される漫画があったとは！
真理のために命をかけた先人たちの物語。
この作品は、現役研究者である私・ぽるこが衝撃を受けた作品として、特に研究者およびこれを志す者には強く本気でオススメします。今ある常識を疑う心、誰に何を言われようと真理を追求する姿勢に触れ、心が動くこと間違いありません。
私自身、世界のトップ研究者だった師匠によく言われた言葉を思い出します。“目の前の現象に楽な答えを持ち出し、疑うことをやめ、真理の追求という困難な道から逃げていないか！？”
本作はこういった研究者の気概なるものを感じる、必読の価値ある一冊です。全8巻ですでに完結していますし比較的手軽に一気読みできます。気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
