これまでいくつかの具体例を紹介しながら、自由体の考え方と力の伝わり方を説明してきたけど、この記事を最後の事例紹介としたい。
この記事で紹介するのは「曲げ・ねじり問題」だ。
曲げやねじりでは、引張・圧縮に比べて簡単に大きな応力が生じるので、破壊の原因になりやすく、非常に重要な負荷形式だ。また、引張・圧縮よりも現象の理解も難しいので、苦手な学生も多いかもしれない。
この記事では、曲げ・ねじりで発生する応力や変形といった詳細の話はしないが、その基本となる力の伝わり方について簡単に説明したい。
その他の具体例は以下の通り。
材料力学 《全員必見・超重要》自由体の考え方（引張・圧縮を受ける棒）【Vol. 1.2-1】
材料力学《全員必見・超重要》自由体の考え方（色んな支持方法）【Vol. 1.2-2】
材料力学《全員必見・超重要》自由体の考え方（トラスの問題）【Vol. 1.2-3】
材料力学《全員必見・超重要》自由体の考え方（異種材料・別部品）【Vol. 1.2-4】
自由体の基礎について再確認したい人は以下の記事を読んでみてほしい。
材料力学 《全員必見・超重要》自由体の考え方の基礎【Vol. 1.1】
- はりの曲げ問題では、曲げモーメントが材料中で変化することがあり、安全設計の観点からはその最大値を知ることが重要である。
- ねじり（トルク）受ける棒では、棒のどの位置でも外力と等しいトルクが働く。
- モーメントは、伝わる材料の向きによって曲げモーメントにもトルクにもなる。
夢へ駆ける少女の姿に感涙！！
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか？」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい！」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanなら2/4までなんと3巻無料で読めてしまいます！まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです！
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
Contents
はりの曲げ
はりの曲げの問題は、材力の教科書の中でまあまあボリュームを取ってるトピックだと思う。それは、引張・圧縮やねじりとは違う事情があり、これが曲げ問題を難しくしているからだ。
この記事では、曲げ現象の細かい話（応力や変形など）はしないが、曲げを受ける材料の中でどんな風に力やモーメントが伝わっていくか、を説明したい。
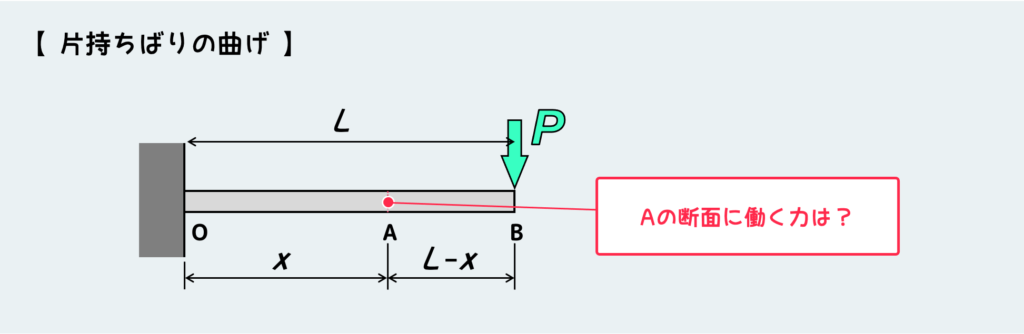
上図のようなはりの曲げを考えよう。片側だけが固定されたはりのことを「片持ちばり」という。
この片持ちばりの先端に荷重がかかると、このはりは当然曲がるのだが、このはりの途中の断面にはどんな力が働いているだろうか？
毎回言っているが、内力を知るためにはその知りたい場所で材料を切って、自由体として切り出したものの平衡条件を考えなくてはならない。
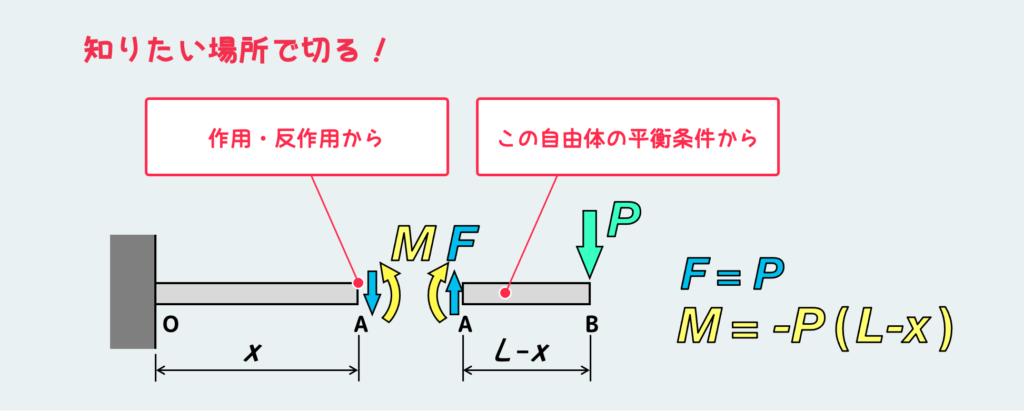
なので、今回はAの断面ではりを切って、切断した右側の自由体の平行条件から、Aの断面に働く内力を決定する。
自由体を切り出して平衡条件を考えると、上のようにAの断面には ”せん断力F” と ”曲げモーメントM” が作用していることが分かる。
（※のちのちSFDとBMDを描くことを念頭において、この図で内力として仮置きしたFとMの向きは定義に従って描いている。）
そして、切断したもう一方の断面（左側のA面）には、作用・反作用の法則から、同じ大きさで反対向きのせん断力と曲げモーメントが作用する。
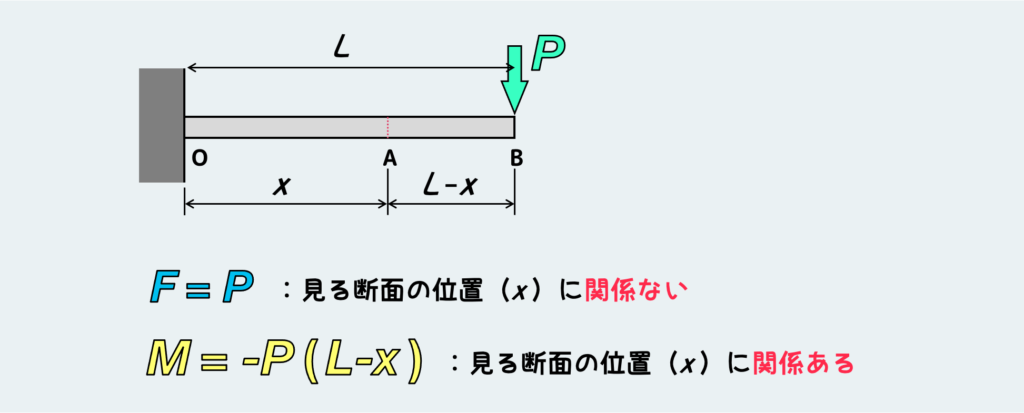
ここで注目すべきことは、『曲げモーメントMは切断した位置（根本からの距離xで表現）に関係する量であり、つまり位置が変わればそこに働く曲げモーメントの大きさが変化する』ということである。一方、せん断力F の大きさは “P” なので “x” に関係のない量であり、どの位置で見ても外力と等しい一定値を取る。
これは、引張・圧縮やねじり問題にはない、曲げ問題の大きな特徴である。
そして曲げ問題においては（細かい説明は省くが）、曲げモーメントがこのはりの受ける応力や変形を（ほぼ）支配している。つまり、内力として材料中を伝わる曲げモーメントを正確に把握することこそ最も重要なことだと言っていい。
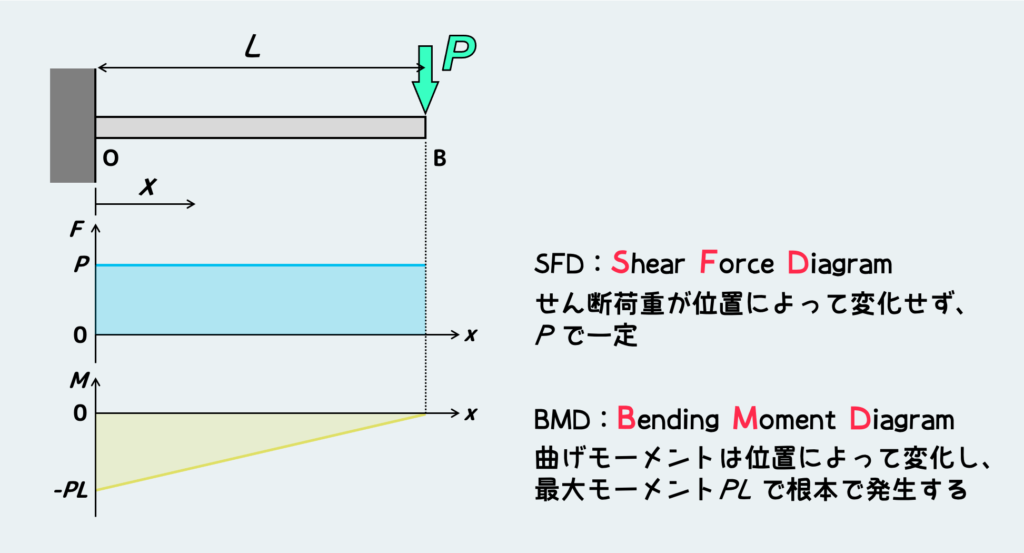
そういうことだから、曲げのトピックの一番最初にせん断応力線図 SFD（Shear Force Diagram）と曲げモーメント線図 BMD（Bending Moment Diagram）を学習する訳だ。これらの線図を描くことは、せん断力や曲げモーメントがどう変化していくかを視覚的に知るために重要になる。
SFDはBMDとある関係を持っているため同時に描くことが多いが、肝心なのはBMDだ。BMDを見れば、その材料中のどこで曲げモーメントが最大になるか？だとか、どこからどこまでは曲げモーメントが一定だとか、そういう情報を簡単に得ることができる。
特に最大曲げモーメントが働く位置、そしてその大きさを知ることは重要だ。なぜなら、最大曲げモーメントが働く場所に最大の曲げ応力が働くことになり、その応力の大きさもモーメントの大きさによって決まるからだ。上の問題の場合は、根本部分に最大の曲げモーメント ”PL” が働くため、根本が最も危険な部位である。
まあ、この問題の場合そんなことは容易に想像できる話なんだけど、もっと複雑な負荷を受ける場合はBMDを描かないと、どこから壊れる可能性があるか？またそこに作用する応力の大きさは？といったことは分からない。
なお、曲げだと必ず曲げモーメントが位置によって変化するかというと、、そんな事もない。どういう場合に曲げモーメントが変化するか？とか、その他色んな問題のSFDやBMDの描き方については別の記事でまとめたいと思う。
SFD、BMDはこれらの事を視覚的に理解するのにとても便利。
棒のねじり
では次に、ねじり問題を考えてみよう。
ねじりも曲げと同じくモーメントに起因する現象だ。ねじりの場合は、曲げモーメントではなく、ねじりモーメントが現象を支配している。ねじりモーメントのことをトルクと言う。
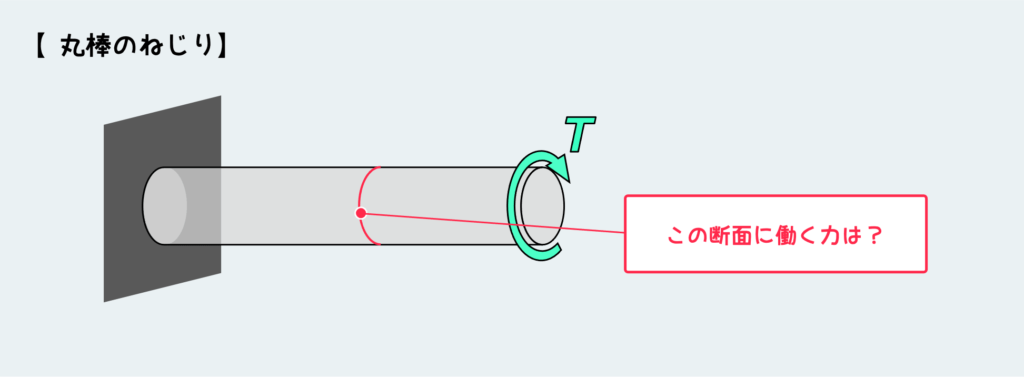
さて、曲げのときと同様に棒の途中の断面に働く内力を考えてみよう。
今回もやはり”知りたい場所で切る”、そして自由体として取り出してから平衡条件を考える。
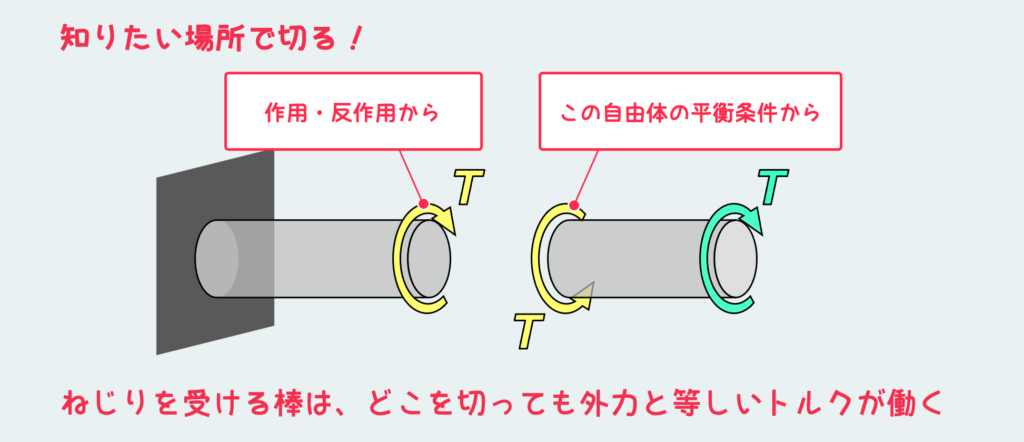
自由体の平衡条件を考えると上図のようになる。つまり、右側の自由体が釣り合うためには、外力として加えられたモノと同じ大きさで反対向きのトルクが、今切断した面に作用する必要がある。
さらに、作用・反作用から左側の断面にも同じ大きさのトルクが働く。
ここで注目すべきことは、『棒のどこで切断してもその断面に働く内力は外力と等しいトルクになる』ということだ。これは、曲げとは大きな違いで、むしろ引張・圧縮と似たような性質を持っている。
ねじり問題では、せん断応力が登場したり、断面上で応力分布が生じたり、極断面二次モーメントを使ったり、もちろん引張・圧縮よりも複雑であることは否めない。だが、この『どの断面にも一定のトルクが伝わる』という特徴のおかげで、曲げ問題よりもずいぶんシンプルになる。
ここではとにかくこの特徴を理解してもらって、応力や変形など詳細は別の記事で解説したい。
曲げとねじりの関係性
ではこの記事の最後に、曲げとねじりの関係性について紹介したい。
結論から先に言うと、ここで伝えたいことは『曲げモーメントもトルクも正体は実は同じもので、見る方向によって曲げモーメントとして働くか、トルクとして働くかが変わる』ということだ。
曲げモーメントやトルク…こいつらの正体ってのはつまりただのモーメントであり、それ以上でもそれ以下でもない。それが場合によっては曲げるように働き、また別のときはねじるように働くという話だ。
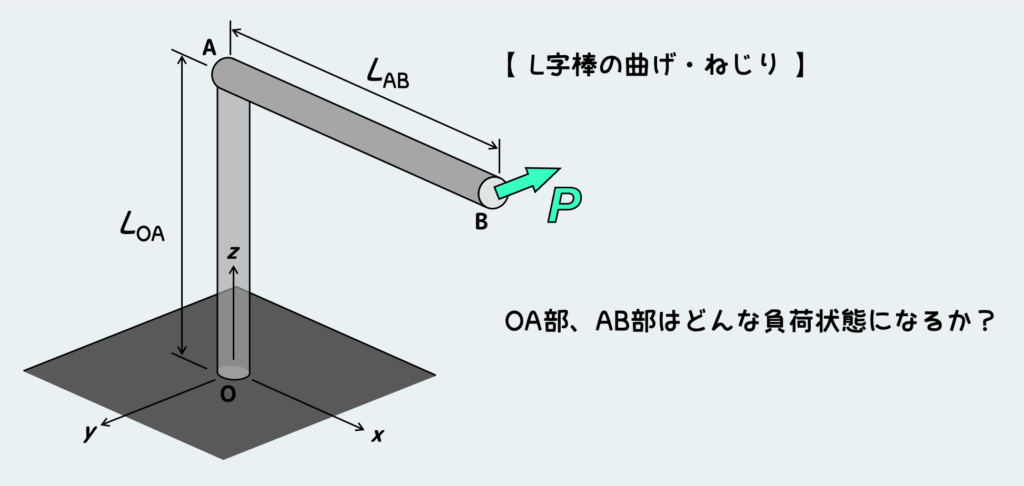
では、このことを理解するためにすごく簡単な例を考えてみよう。
上の図のようにL字に曲がった棒の先端に荷重をかける。このとき、OA部とAB部はそれぞれどんな負荷状態になるだろうか？
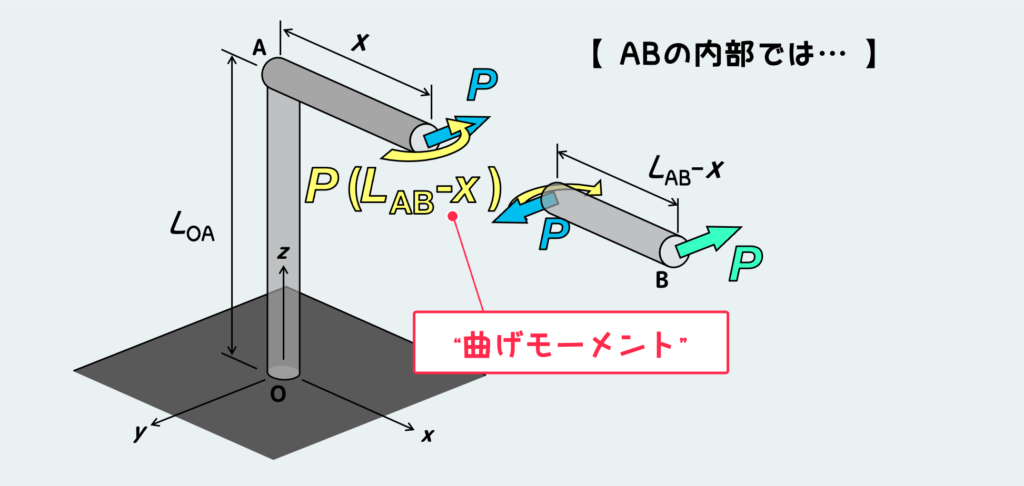
AB部のどこか適当な断面（Aからxの距離）で切ってみると、自由体図は上のように描ける。
すなわち、この断面にはせん断力（図中の青）とモーメント（図中の黄色）が作用している。
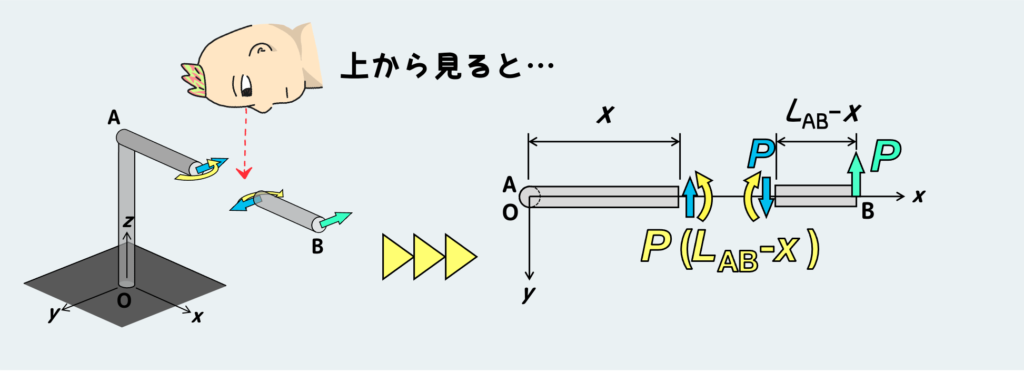
三次元の絵が少し分かりにくい人は、上から見たときの絵を描くと分かりやすくなるかもしれない。
そうすると「これはどこかで見た事あるな」と思うはずだ・・・そう！この記事の一番最初に説明した「はりの曲げ」にそっくりだと気付けるだろう。このL字棒のAB部分は、先端に荷重を受けるはりの曲げ問題と同じ状態になってるという訳だ。
ABの内部には、外力Pに起因するモーメント（図中の黄色）が伝わっていくが、これはABを曲げようとするモーメントなので、AB部にとっては『曲げモーメント』として働いている。
では次に、これがOA部にはどう伝わるかと考えよう。
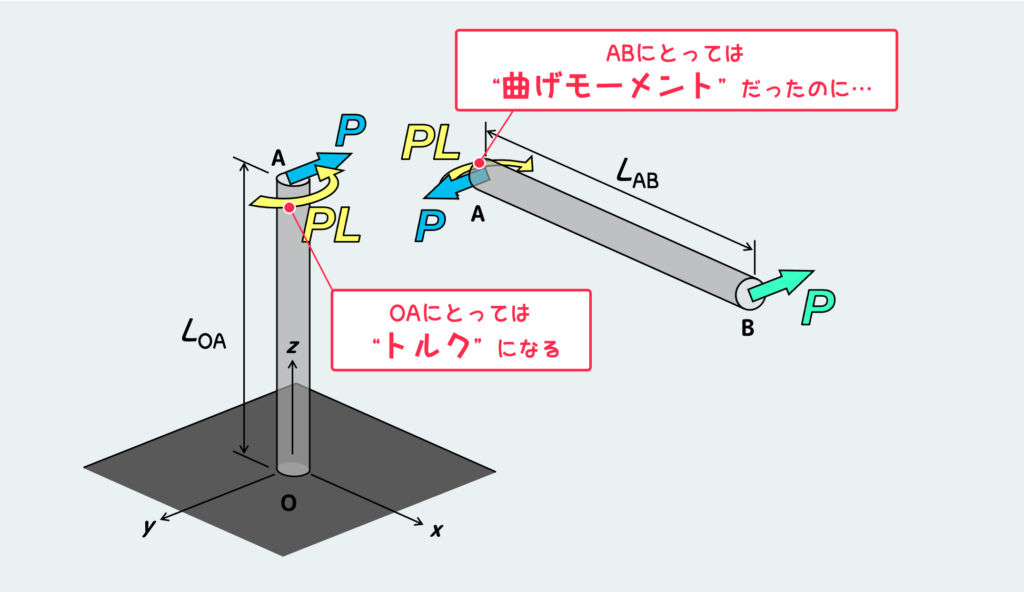
切断する場所をABの途中のどこかではなく、Aの位置まで移動していこう。すると、自由体図は上図のように描ける。さっきのABの途中で切った時と比べて、モーメントの大きさが変わっているが、せん断力（図中の青）とモーメント（図中の黄色）が伝わっていることは変わらない。
しかし、OA部の方に伝わるモーメントにはある変化が起きている。OAの方の切断面Aには、作用・反作用から反対向きの力とモーメントが働くが、このモーメントはOAをねじるように働いている。AB内部を曲げモーメントとして伝わってきたものが、材料の向きが90度変わると、ねじるようなモーメント（つまりトルク）として働くようになる。
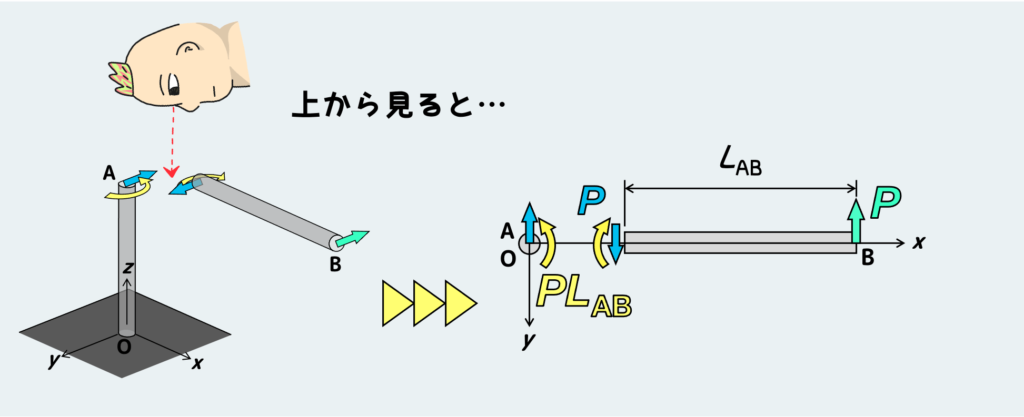
これもやっぱり、上から見た絵を描いた方が分かりやすいかもしれない。
AB部に働いていた曲げモーメントの作用・反作用を考えると、同じx-y平面上で向きが逆になる（時計回り→反時計回り）ので、図のようにOA部の先端Aにトルクが働く。
このように、モーメントというのは作用・反作用の法則が適用されるときに向きが逆転するのみで、存在する面（今回の場合はx-y平面）が変わることはない。しかし、材料の向きが変わることによって、『曲げ』にもなるし、『ねじり』にもなる。場合によっては『曲げ＆ねじり』になることだってある。
最後にOAの内部では、どう内力が伝わっていくかを確認しよう。
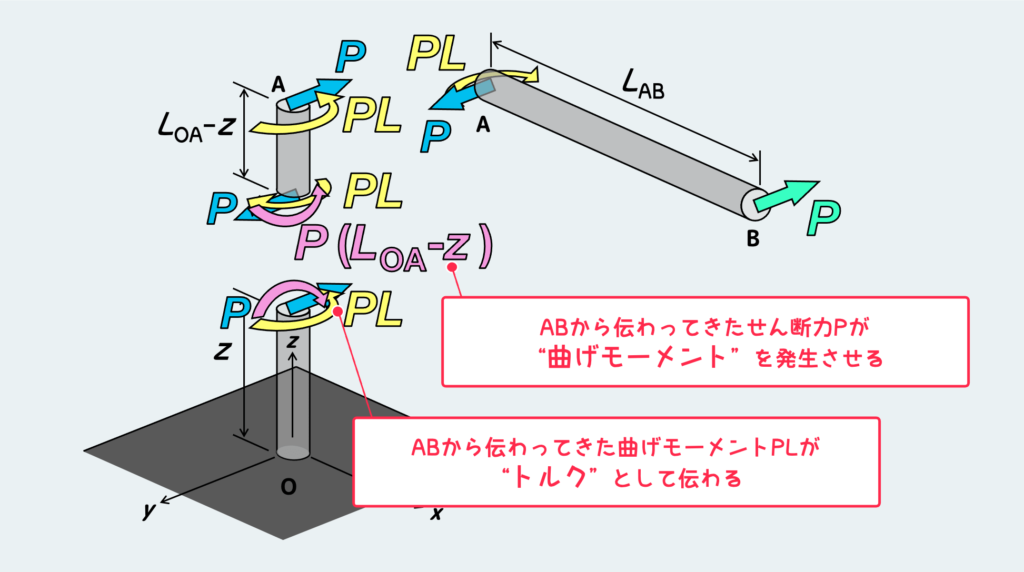
OA部のどこか途中の位置（Oからzの距離）で切って、自由体図を描くと上のようになる。
この断面には、せん断力（図中の青）とトルク（図中の黄色）と曲げモーメント（図中のピンク）が作用している。曲げモーメントは、OAの先端Aに作用しているせん断力Pによって発生したものだ。
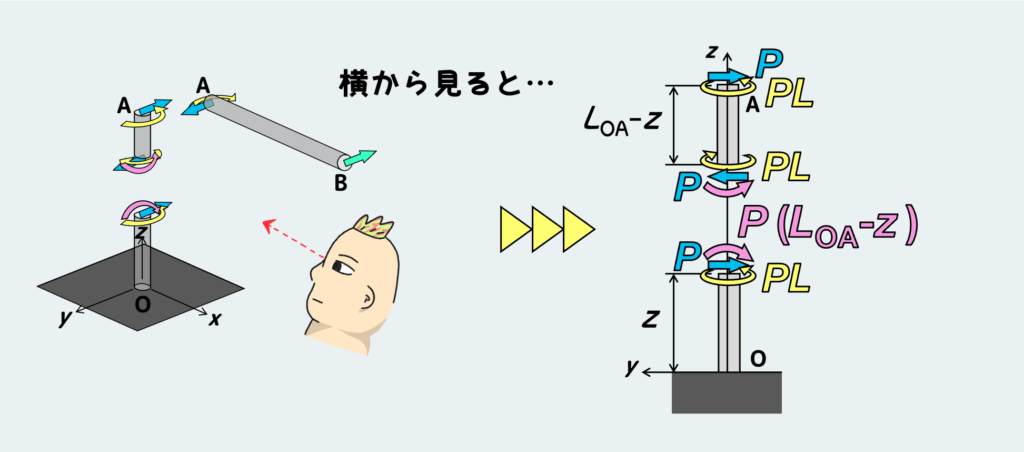
これも横から見た絵を描いてみると、上のようになる。
つまり、OA部は『先端に荷重Pを受けるはりの曲げ問題』と『トルクPLを受ける棒のねじり問題』が重なったような状態になってる訳だ。
まとめ
最後に説明した問題は組合せ応力の問題と言って、変形を考えるにしても応力を考えるにしても少し骨がおれる。しかし、実際の構造部材はこういった複雑な問題が多いので慣れないといけない。
大事なことは、これまでの記事で説明してきたように自由体図を描いて、どこの部分にどういう内力が伝わっているかを正確に把握すること。そしてそれを元に、引張・圧縮、曲げ、ねじりといった基本問題の組合せに置き換えて考えることだ。
この手順をしっかり理解すれば、基本的にどんな問題もすんなり解けるだろう（もちろん問題によっては計算量が膨大だったりすることはある…）。
という訳で、ここまで５回の記事で、自由体の考え方つまり内力の把握の仕方を長々説明してきたが、今回でひとまず終わりにしたい。次回からは、変形や応力を考えたりする問題を対象に解説をしていきたいと思う。ぜひご一読いただきたい。
- はりの曲げ問題では、曲げモーメントが材料中で変化することがあり、安全設計の観点からはその最大値を知ることが重要である。
- ねじり（トルク）受ける棒では、棒のどの位置でも外力と等しいトルクが働く。
- モーメントは、伝わる材料の向きによって曲げモーメントにもトルクにもなる。
研究者を志す者 必読！！
全8巻完結
こんなにも知的探究心を刺激される漫画があったとは！
真理のために命をかけた先人たちの物語。
この作品は、現役研究者である私・ぽるこが衝撃を受けた作品として、特に研究者およびこれを志す者には強く本気でオススメします。今ある常識を疑う心、誰に何を言われようと真理を追求する姿勢に触れ、心が動くこと間違いありません。
私自身、世界のトップ研究者だった師匠によく言われた言葉を思い出します。“目の前の現象に楽な答えを持ち出し、疑うことをやめ、真理の追求という困難な道から逃げていないか！？”
本作はこういった研究者の気概なるものを感じる、必読の価値ある一冊です。全8巻ですでに完結していますし比較的手軽に一気読みできます。気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
