材料力学　（kgf）から（N）への変換など単位のキホンその１【材力 Vol. 0.1】

材料力学の単位を落としそう…という学生は意外と超初歩のところでつまずいているのかもしれない。超初歩って何かというと、「単位」を正しく使えていない、ということだ。卒業に必要な単位のことではなく、数値の後ろに付く【kgf】とか【N】とか、そういう奴らのことだ。

もちろんこれは本題ではない。しかし、ある意味本題以上に重要であることに疑いの余地はない。材料力学は数学ではなく、工学のなかの実際の問題を扱った学問であるからだ。

単位を正確に理解していなければ、材料力学の問題を『数学的に』解くことができたとしても無意味だ。むしろ危険ですらある。

そして卒業に必要な必修の単位も落とすことになる。

そうならないためにも、この記事を読んでしっかり単位について理解してほしい。

単位を間違えると何が起こる？

例えば…だ。ある材料に負荷しても良い限界荷重を（何も考えずに公式に数値を代入して）求めた結果、100 という数字が出てきたとしよう。これの単位は 100【N】だろうか？それとも 100【kgf】だろうか？何も考えずに単位をつけていないだろうか？

後で詳しく説明するが、100【N】と100【kgf】には約10倍の開きがある。つまり、よくわからないまま単位を誤って使用すると、材料が耐えられるギリギリの荷重の約10倍の荷重を負荷してしまう、といったことも起きてしまうということだ。テストの解答としては当然バツだし、実際の設計だと事故につながるような致命的なミス（ーだからすこぶる減点したくなる）になってしまう。

実際のところこういう単位に気を配らない学生は山のようにいるんだけれど、単位の正しい使い方まで細かく指導してくれる先生は少ないのかもしれない（ーだいたいそういうミスの多い学生に限って教えたことを素直に聞かない子だったりするわけだけど……）

ぽるこ

公式を覚えていたり、計算だけができても、単位のところで間違えると意味がなくなっちゃうってことだね。

いかろす

あんまり気にしたことがなかった。。

ぽるこ

ミスが多い人はこれを機会に一度単位について見直して見てね。

材料力学に登場する単位たち

材料力学ではどんな単位が登場するだろう。扱う物理量としては、寸法や変位なんかの長さに関するもの、角度、質量、力（荷重）、モーメント、応力、ひずみ……があるので、これに対応する単位を扱えるようになる必要がある。

質量

おもに【kg】（キログラム）を使用する。時折【ton】（トン）も使うことがあるが、1【ton】= 1000【kg】だ。基本的に材力では、質量自体を公式に入れることはないので、重要なのは次の「力」だと思う。

力（荷重）

おもに【N】（ニュートン）や【kN】を使用する。もしくは【kgf】（キログラムフォース、キログラムジュウ）もよく使う。【kgf】というのは、物体の質量【kg】に似ているが、物体の（地球上の）重量（重力）を表したもので、1【kgf】は文字通り 1【kg】の物体が地球で受けている重力のことだ。もし君が体重50【kg】のかわいい女の子をお姫様だっこしているとしたら、君の両腕が受けている力は50【kgf】ということになる。

ただし、材力の公式を利用する場合、絶対的におすすめなのは【N】だ。【kN】ではなく【N】を使うのがポイントだ。なぜかは次回以降に説明するとして、ここでは【N】と【kgf】の変換について見てみよう。

【N】と【kgf】の変換について

1【kg】のおもりをある材料にぶら下げると、この材料が受ける力はさっき言った通り1【kgf】だ。これを【N】に変換すると、受ける力はいくらになるだろう？答えは約 9.8【N】だ。簡易的には、1【kgf】= 10【N】と覚えておけばOKってことだ。

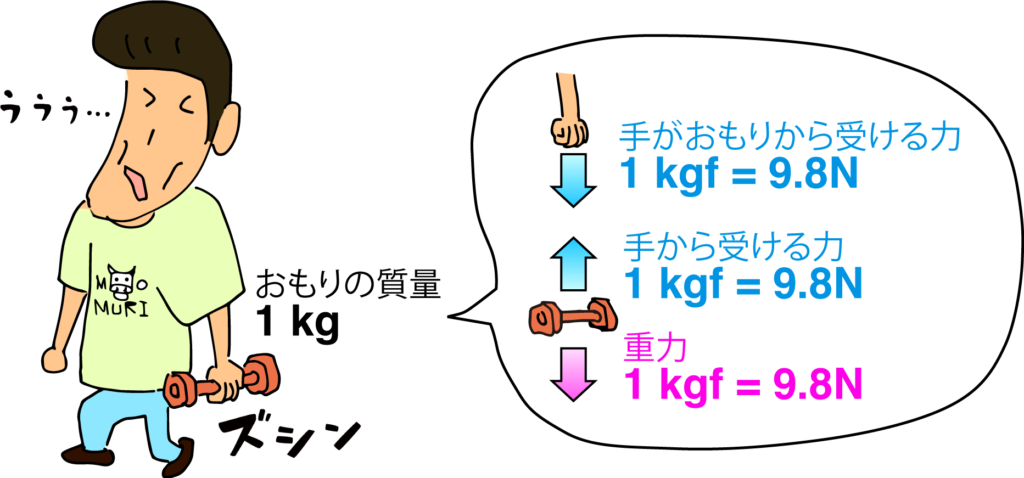
なんで 1【kgf】= 約 10【N】なの？

長さ、伸び、縮み

物体のサイズ（寸法）を表したり、変形量を表したりする。この世界では、使う単位はおもに【mm】（ミリメートル）。

変形量を表す場合は、【μm】（マイクロメートル、ミクロン）や【nm】（ナノメートル）も使うことが多い。【μ】というのは 10^-6という意味だから、1【μm】= 1/1000000【m】= 1/1000【mm】ということになる。【n】は 10^-9という意味でさらにスケールが小さい。

小さすぎて全然イメージが湧かないと思うけど、材力で扱う材料の変形量ってのはそのぐらい小さいということだ。

反対のことを言うようだけど、大きく変形できるのは金属材料の素晴らしい特徴だ。実際に見たことがある人は少ないかもしれないが、金属はぐにゃりと曲がったり、伸びたりすることができるおかげで、色々な形に加工することができる。でもあくまで材力の範囲では、そういう大きな変形は基本的には扱わない。

角度

角度は、人と話したり誰かに説明したりするときは普通は【°】（度）を使う。だけど、公式の中だったり数学的に取り扱うときには【rad】（ラジアン）を使うので、【°】と【rad】の関係性を理解しておくことが重要だ。つまり…

角度【rad】についてもう少し詳しく知りたい人は、以下の別記事に詳しく書いているので覗いて見て欲しい。

角度の単位（rad）とは？【番外１】

また、これに関連する話として、sinθやtanθをθで近似することがある（θがとっても小さいときという条件付きで）。これは材力に限った話ではないけど、材力でも頻繁に登場するので、なんでそうなるのか理解できない人は以下の記事を読んでみるとスッキリするかもしれない。

「sinθをθで近似する」ってどうしてそうなるのか詳しく説明します。【番外２】

まとめ

最初に言ったように、単位を間違えてしまうと正解から大きくかけ離れた答えを導いてしまうかもしれない。単位を使いこなすことは材料力学（というよりもすべての理工学）の大前提であるわけだ。

今回は材料力学に登場するいくつかの物理量について単位を説明してきたが、しっかり理解できただろうか？次の記事では、応力、ひずみ、モーメントについても解説していきたい。