材料力学《全員必見・超重要》自由体の考え方（色んな支持方法）【Vol. 1.2-2】

今回の記事は自由体の考え方の具体例第２弾ということで、支持方法にも注目しようという話だ。では早速本題に入ろう。

その他の具体例（一部執筆中）は以下の通り。

材料力学　《全員必見・超重要》自由体の考え方（引張・圧縮を受ける棒）【Vol. 1.2-1】

材料力学《全員必見・超重要》自由体の考え方（トラスの問題）【Vol. 1.2-3】

材料力学《全員必見・超重要》自由体の考え方（異種材料・別部品）【Vol. 1.2-4】

材料力学《全員必見・超重要》自由体の考え方（曲げ・ねじり問題）【Vol. 1.2-5】

自由体の基礎について確認したい人は下の記事を読んでほしい。

材料力学　《全員必見・超重要》自由体の考え方の基礎【Vol. 1.1】

支持方法によって反力は変わる

当たり前と言えば当たり前かもしれないが、支持方法に応じて、構造体が支点から受ける反力の種類は変わる。このことをよく理解していないと、自由体図を描いたときに余計な力を描き込んでしまい、正しく内力の伝わりを把握することができなくなる。（というか解けなくなる）

これから紹介する支持方法の種類を見て、そこに働き得る反力を理解しよう。

ピン支持

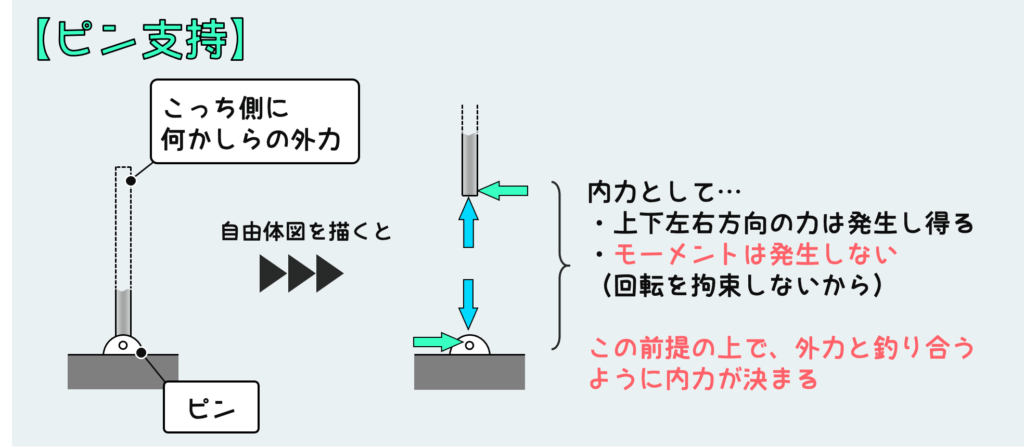
まず、ピン支持だ。

ピン支持の特徴は「回転を拘束しない」ことだ。支点では、動きを拘束することで力が発生するので、回転の動きを拘束しないということは回転モーメントを支えられないことを意味する。

つまり、ピン支持ではモーメントが反力として伝わることはなく、発生し得る反力は水平方向と垂直方向の２種類の荷重のみだ。

ピン支持＋コロ

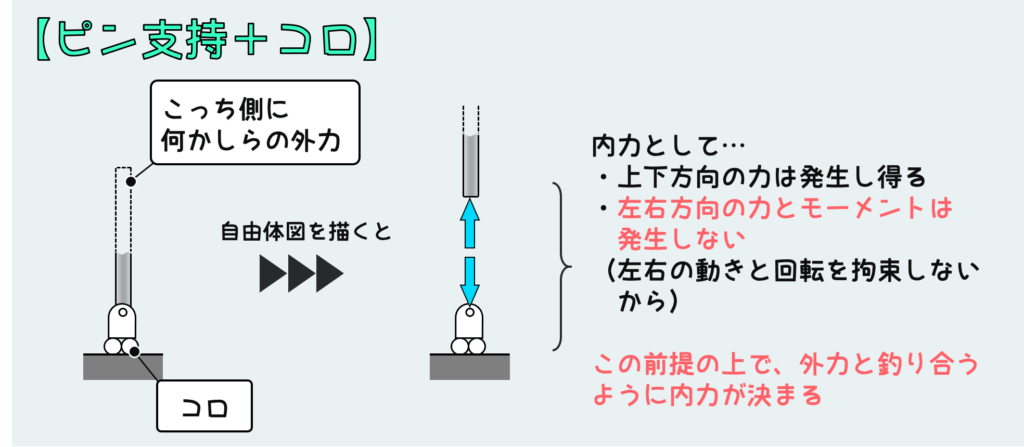
場合によってはピンにコロが付いている場合がある。

コロが付くと、地面に対して平行な方向の動きを止められない。つまり、回転だけでなく横方向の動きも拘束しないので、モーメントと横方向の荷重を支えられない。

すなわち、ピン＋コロのときは横方向荷重とモーメントが反力として伝わることはなく、垂直方向荷重のみが発生し得る。

固定支持

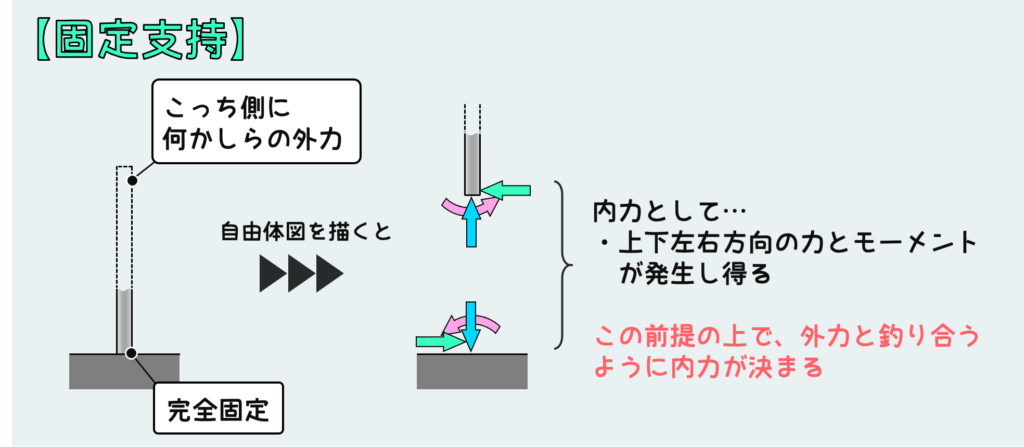
固定支持の場合は、すべての動きが拘束される。

なので、すべての荷重・モーメントを支えることができる。よって、上下左右方向の力とモーメントが反力として発生し得る。

ナイフエッジ

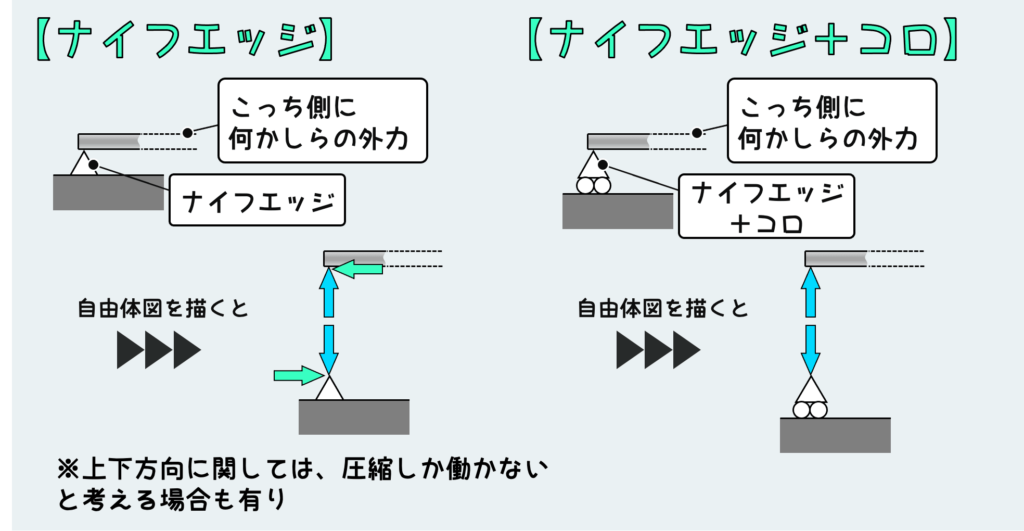
はりの曲げのような問題でよく登場するのがナイフエッジだ。

とんがったエッジの上に材料を乗せただけ、というような支持方法だ。ただこれをリアルに想像してしまうと、横方向の動きを拘束せずに横方向の荷重を支えられないことになってしまうが、材力の問題の中でナイフエッジが登場するときは横方向の動きを拘束するとみなすのが基本だ。

横方向の動きを拘束しないときは、そのことをちゃんとコロを付けて表現する。誤解が生まれないように、横方向の拘束については表現のルールが決まっている訳だ。という訳で、横方向の荷重を受けられるかどうかは、コロの有り無しで決まる。コロが付いてないナイフエッジの場合は左右方向の荷重が反力として働き得るが、コロが付いたナイフエッジの場合は左右方向の力は反力として働かない。

垂直方向の荷重については微妙な話だが、リアルなナイフエッジの場合は圧縮荷重（押しつける力）は支えられるが引張荷重（引き離す力）は支えられない。しかし、材力のペーパーテストのような問題の場合は出題者がそこまで厳密に考えていない可能性もあり、圧縮も引張も垂直方向の荷重を支えられる設定にしているかもしれない。

このサイトでは、紛らわしいのでナイフエッジの表現は基本的に使わず、ピン支持を使いたいと思う。

ワイヤーで吊る

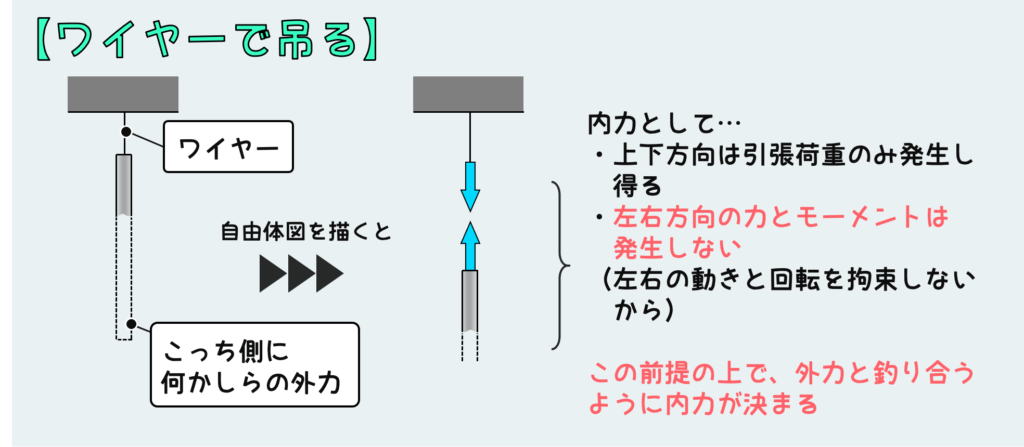
場合によってはこんな支持方法もある。ワイヤーなどの細い紐で吊っただけ、というやつだ。

ポイントは、この紐が細いことで、横方向の荷重および上下方向の圧縮荷重を支えることができないという事だ。横向きの動きに対しても、上向きに圧縮するような動きに対しても、このワイヤーはたゆむだけで支えとしては働かない。もちろんモーメントも支えられない。なので、反力として発生するのは、支持面に対して垂直方向の引張荷重だけということになる。

なお、これが太く、しっかりした剛性をもった材料であれば、もちろん横方向の荷重や圧縮荷重も受けられるようになる。支持面との接続方法によってはモーメントも、である。（ペーパーテストの場合は、この材料が細いのか太いのか、ちゃんと明記されるはずだ。）

いくつかの具体例

では、上記の支持方法について、実際の問題ではどんな風に取り扱うのか、いくつかの具体例を使って説明したい。

具体例その１

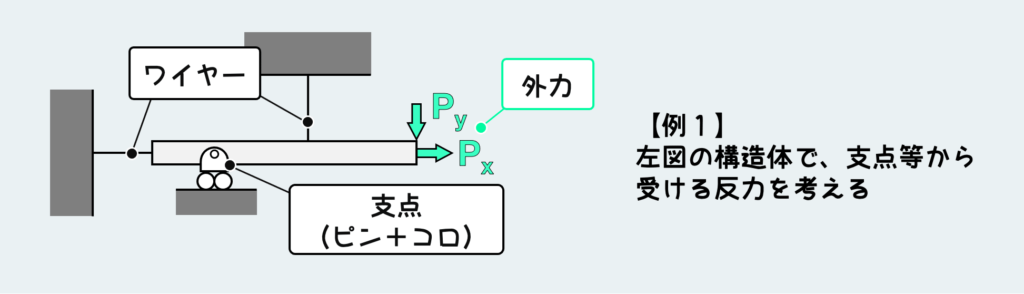
上図のような問題を考えよう。この例では２ヶ所ワイヤーで吊られていて、コロが付いたピンで支持されている。まずは、支点からの反力が知りたいので、知りたい点…つまり支点と繋がっていた部分を切り離して、自由体を取り出す。

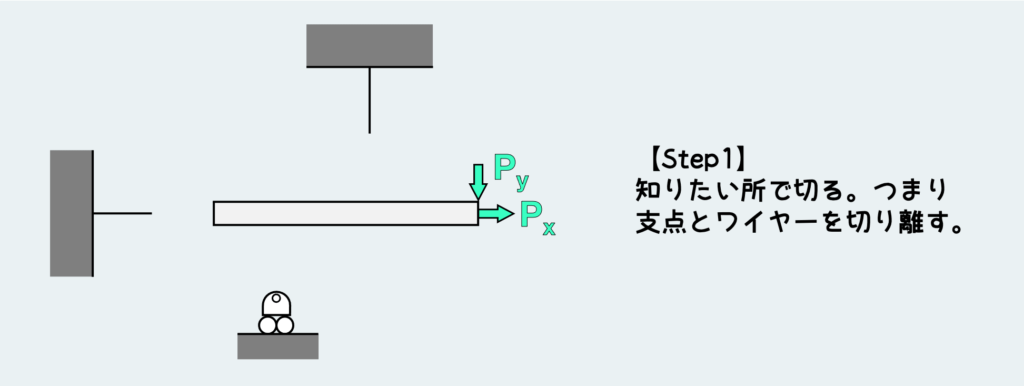
自由体を切り出して描くとこんな感じになる。作用していた外力はそのまま描き込めば良い。

さあ、この状態ではもちろん材料のつり合いが取れていない。なので、外力の作用している方向に飛んでいってしまう。そうならないためには、この材料のつり合いが取れるように、今切り離した支点から力を受ける必要がある。

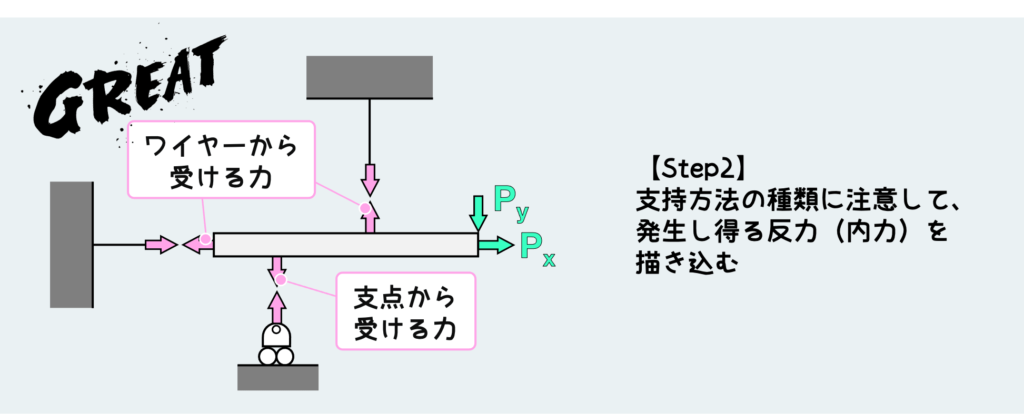
元々繋がっていた支点から受ける力を反力（内力）として描き込んでいく訳だが、ここでとても重要なことは支持方法に応じて発生し得る力だけを正しく描き込むことだ。

ちゃんと正しく支持方法の種類を意識すると上図のようになる。ワイヤーからは、その長手方向に引っ張るような力しか働かないので、図のようになる。また、ピン＋コロは地面に対して平行な力は支えられないので、地面に垂直な力だけが働く。なお、このピン＋コロから受ける上下方向の力の向きはどちらに仮定しても良い。テキトーで良いってことだ。もちろん動きや力のかかり方を想像して「こっち向きの力がかかりそうだな」という向きに置いても結構だ。もしその考えが間違っていたとしたら、平衡条件からこの力を決定したときに負（マイナス）の力として導き出されるだけだ。

さて、この例では未知の力（支点からの反力）が３つ出てきた。これに対して使える平衡条件式は同じく３つだ（水平方向・垂直方向・回転）。なので、平衡条件式３つの連立方程式を解けば、この３つの反力を決定することができる。こういう問題を静定問題という。

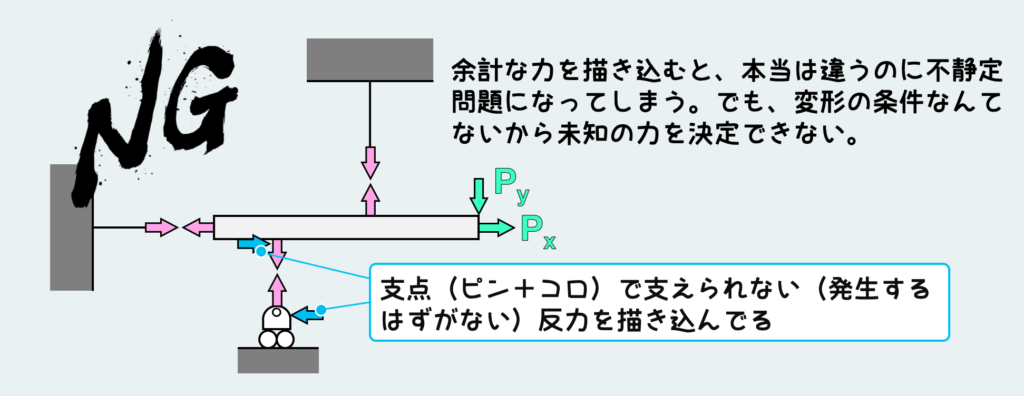
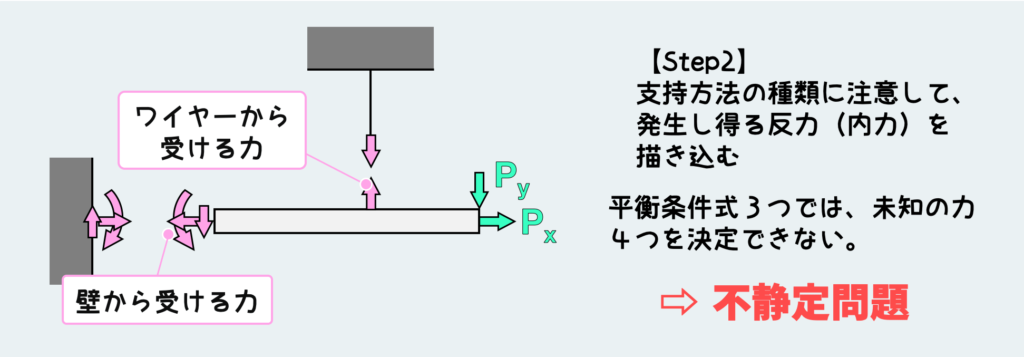
仮に支持方法の種類を何にも意識せずに、テキトーに反力を描き込んだらどうなるだろう？上図では、本来ピン＋コロが支えることのできない、つまり発生するはずがない反力（水平方向の力）を描き込んでしまっている。

この場合、未知の力が４つになってしまう。一方、使える平衡条件式はやはり３つのままだ。つまり、解けない。

このように、ちゃんと状況を把握・理解せずに自分勝手に力を描き込んだりすると、本来解ける問題が解けなくなる。もしもここから強引に解き進もうとすると、ありもしない嘘の条件を作り出すことになり、何かしら解を導き出せたとしても、それはもはや違う問題の解になってしまうことだろう。

具体例その２

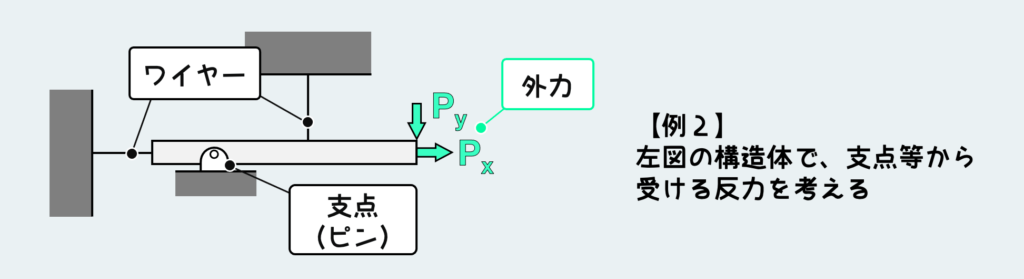
次の例として、上のような問題を考えてみよう。

具体例その１と大きくは変わらない。変わったのはピン支持の所のコロがなくなったことだ。

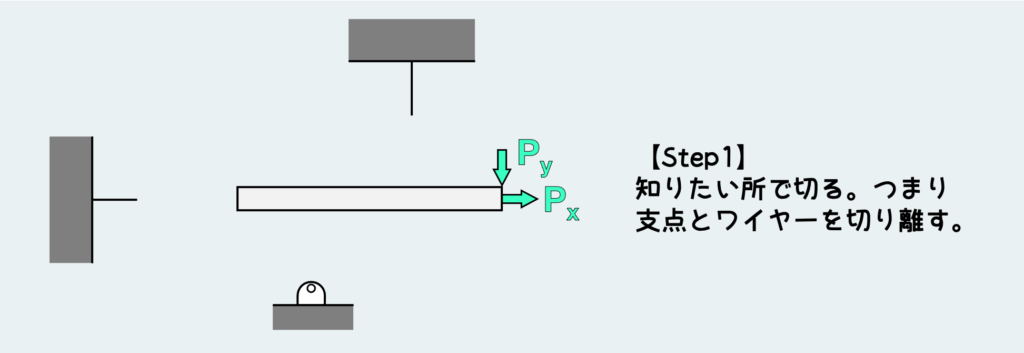
基本的な流れは変わらない。今反力が知りたいので、支点と繋がっている部分を切り離して自由体図を描く。

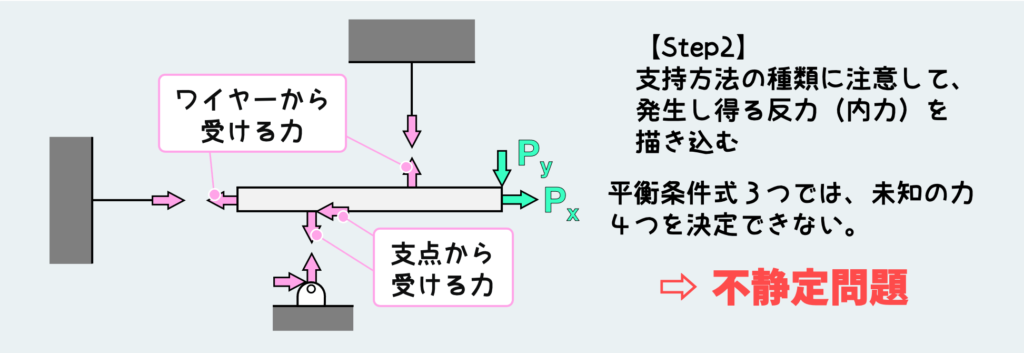
次に発生し得る力を描き込んでいく訳だが、さっきの例と違って今回は、ピンにコロが付いていないので、ピン支持の部分では地面に対して垂直方向の力だけでなく、水平方向の力も働く可能性がある。

こうなると力を正しく描き込んでいるが、未知の力が４つになり平衡条件だけでは本当に解く事ができない。このように、正しく力を描き込んでも平衡条件だけでは力の伝わり方を決定できないような問題を不静定問題といい、未知の力を決定するためにもう一つ条件式が必要になる。それが、変形の条件だ。変形の条件を見つけるためには、この構造体が外力を受けた結果、どんな変形・動きをするか…特に「どこの変形が制約を受けるか？自由に変形できない状況にあるか？」を想像することが必要だ。

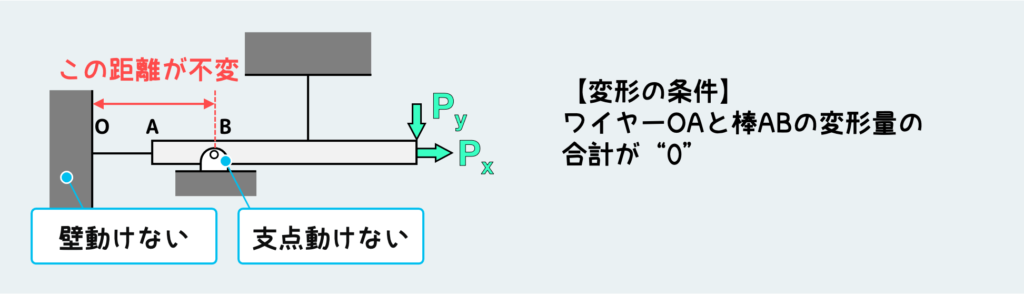
今回の問題では、壁と支点が動けないことがポイントだ。壁と支点が動けないということは、この２点間の距離が変わらないことを意味している。つまり、上図のワイヤーOAと棒ABの長さの合計が常に一定でなければならない。これを実現するためには、OAが伸びたとしたら、同じだけABが縮む必要があるし、逆にOAが縮んだら同じだけABが伸びないといけない。

さて、そんな変形は成り立つだろうか？

結論としては、そういう変形の仕方は無理だ。自由体を切ってOAB間に働く力を考えてみれば良いが、OABの間に伝わる力は引張であればどこも引張荷重が、圧縮であればどこも圧縮荷重が働く。なので、ワイヤーOAが伸びるのであれば棒ABも伸びてしまう。てことは、さっき言ったような変形の条件を満たせない。

ではどうしよう？……もう一つの解決策は、ワイヤーOAも棒ABも変形しないことだ。こうすれば、壁と支点間の距離が変わらないという制約を満たすことができる。

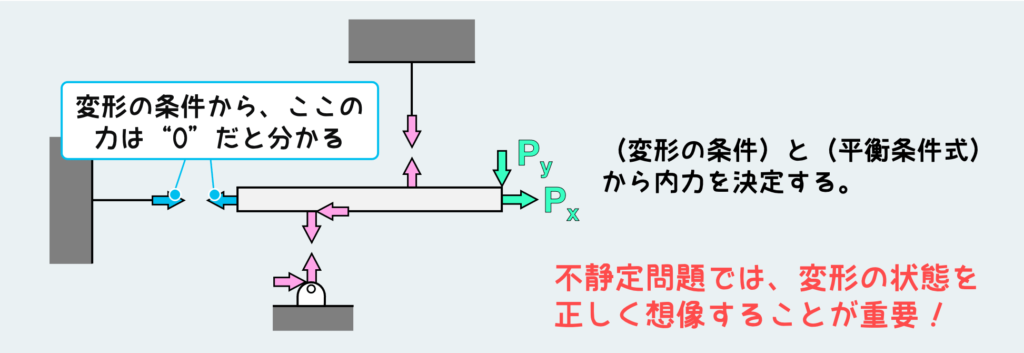
つまり、OAB間に一切の力が働かなければいいわけだ。という訳で、横のワイヤーから受ける反力は”0″である必要がある。これが分かれば、残りの未知の力３つに対して平衡条件式３つが使えるので、すべての反力を決定することができる。

具体例その３

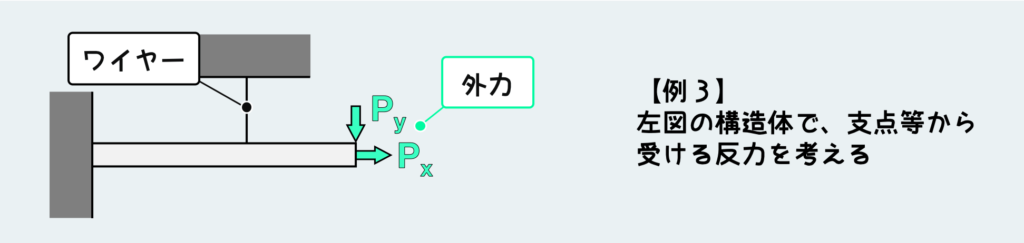
はい。では次はこんな問題を考えてみよう。

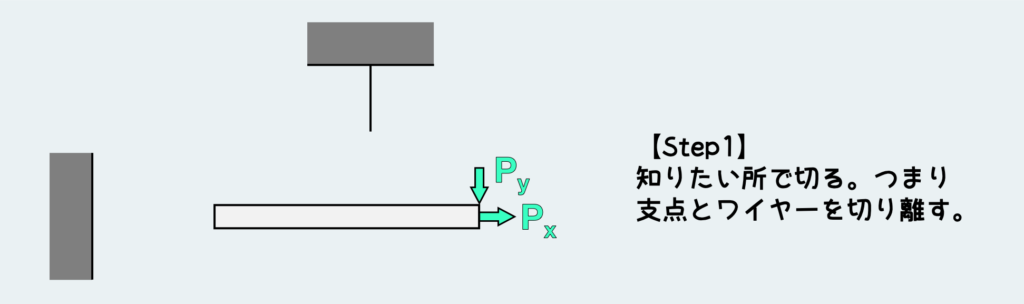
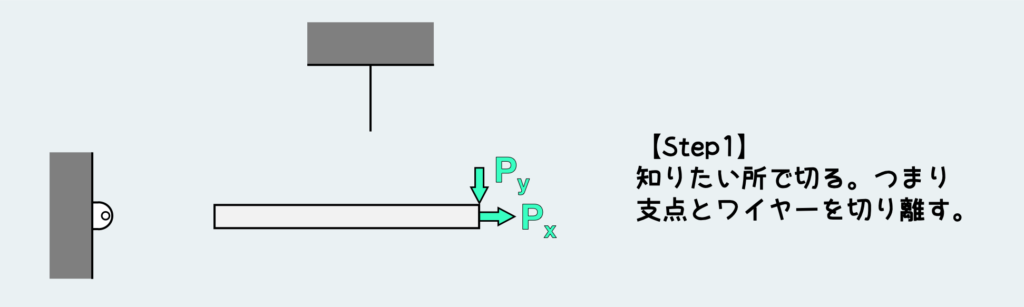
やることは本当いつもと同じだ。知りたい所で切る。

そして、発生する可能性のある力を、今切った部分に描き込む。

今回の問題では、壁から固定支持を受けてるので、壁から受ける反力の種類は縦横の荷重とモーメントの３種類だ。そうすると、今回も不静定問題になるわけだ。

さっきの例でも言った通り、不静定問題では変形の状態を想像することが重要だ。

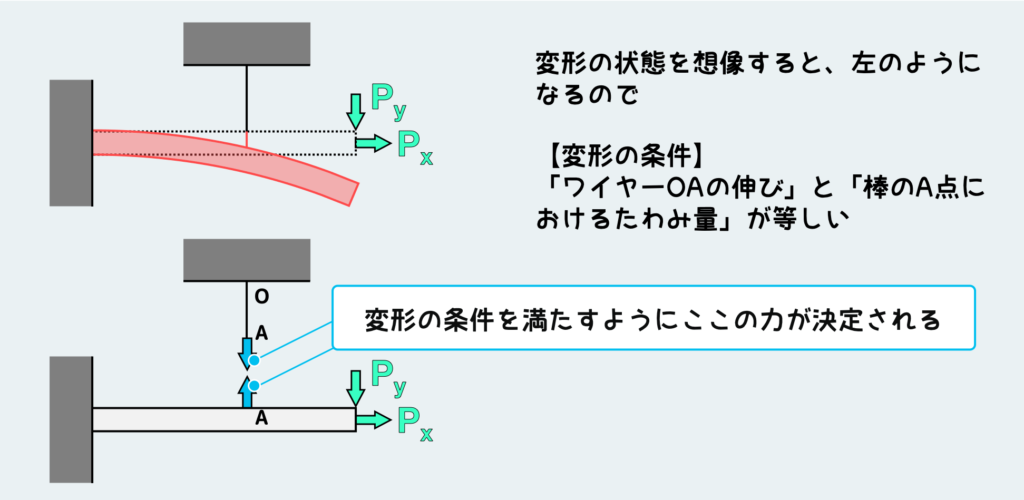
今回の問題では、変形した後の状態は上図のようになる。この図をよく見て、どこの変形に制約がかかるか？を考えて、その制約を数式化しなければならない。

結論としては、ワイヤーの先端と棒がA点で接続されてるので、「ワイヤーの伸び」が「棒のA点におけるたわみ量」と等しくなる必要がある。それぞれの変形量を未知の力を使って表現して、それらが等しいという式を作れば、変形の条件式が出来上がる。

具体例その４

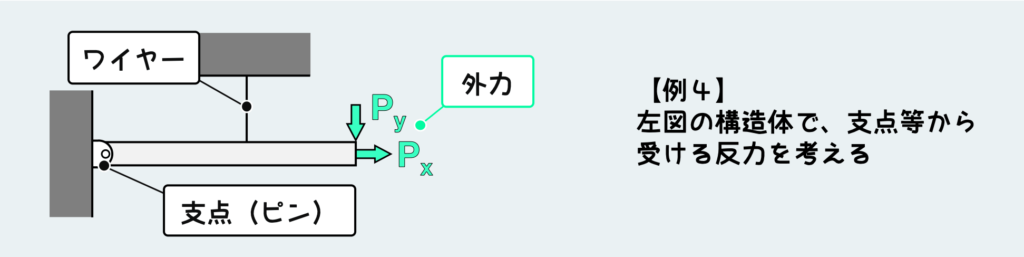
では最後の例だ。さっきの具体例３の壁の固定支持がピン支持に変わったバージョンだ。

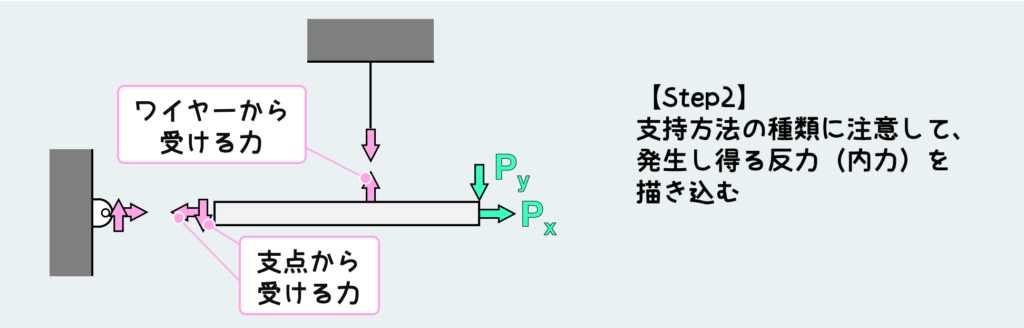
ピンの場合は、モーメントを支えることができないので、壁のピンから受ける反力は縦横の荷重の２種類のみだ。今回は静定問題なので、平衡条件だけで反力すべてが決定できる。

まとめ

今回の記事では、支持方法によってどんな違いが出るかを詳しく見てきた。

ちょっとしたことだが、ちゃんと理解していないと正しく問題を解くことはできない。これを機会にしっかりと見直してみてほしい。