今回からVol.4に突入するが、Vol.4のテーマは『せん断応力』だ。
せん断応力は引張・圧縮応力のような垂直応力と比べると、少しとっつきにくく感じるかもしれない。
この記事では前の記事（Vol.2-1 応力とは？）で説明した、そもそもせん断応力って何なのか？をおさらいしつつ、具体的にせん断応力が問題になるような場面をいくつか取り上げて説明したい。
今回の記事では特に、ピンやリベット、ボルトなどのパーツを使って部材同士を接続しているような場合に、これらのピンなどに働くせん断応力について説明していく。
せん断応力が問題になるもう一つの主要な例として『ねじりを受ける部材』があるが、これは次の記事で詳しく取り上げたいと思う。
（記事執筆中）
- せん断応力は、ある面に対してその面に沿うような方向に働く応力であり、ピン等で部材同士を接続している場合や材料にねじり負荷を加えるような場合に問題になる。
- ある面を境にして材料の移動方向が逆転する・かつその移動方向がその面に沿うような方向の場合には、その断面にはせん断力が作用している。
- このせん断力によるせん断応力は断面上に一様に発生し、その大きさはせん断力をピン等の断面積で割ったもので定義される。
せん断応力とは面に沿った方向に働く内力（せん断力）に起因する応力
垂直応力（引張応力や圧縮応力）は比較的イメージしやすいと思うが、せん断応力については、少し取っ付きにくいと感じるかもしれない。
引張応力や圧縮応力がある面に働く引張や圧縮の内力に起因していことと同じように、せん断応力はせん断の内力（今後”せん断力”と呼ぶ）に起因するものである。せん断力はある面に対してその面に沿った方向に働く内力であり、せん断応力も当然同じように面に沿った方向に働く。
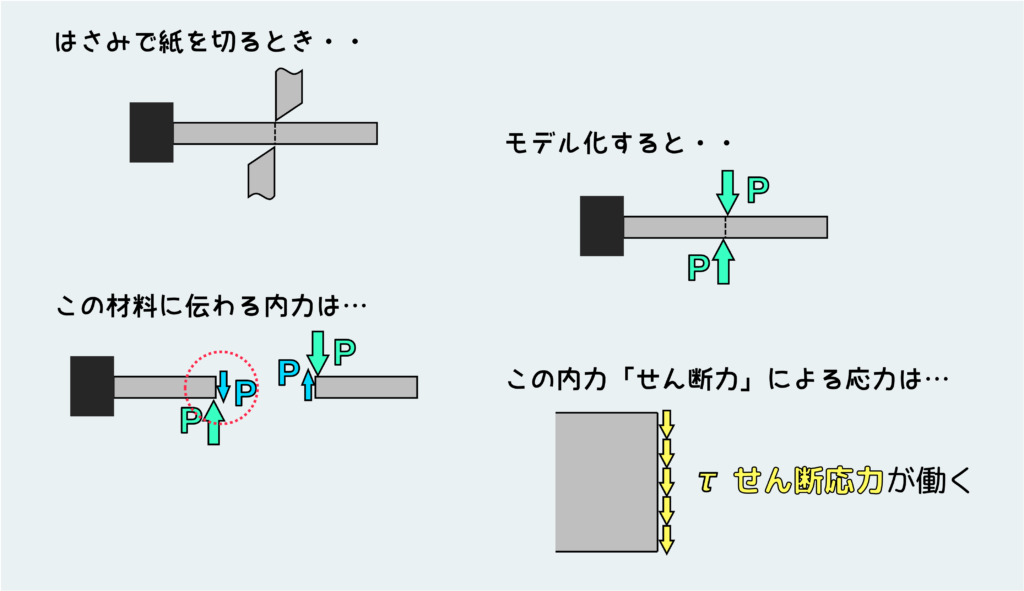
一番身近なところでせん断力およびせん断応力が登場するシーンといえば、はさみで紙を切るときだろう。はさみで紙を切るときの状態をモデル化して描くと図のようになる。はさみで切断される面（刃と刃の境目の面）には図のように応力が働き、これがせん断応力な訳だ。
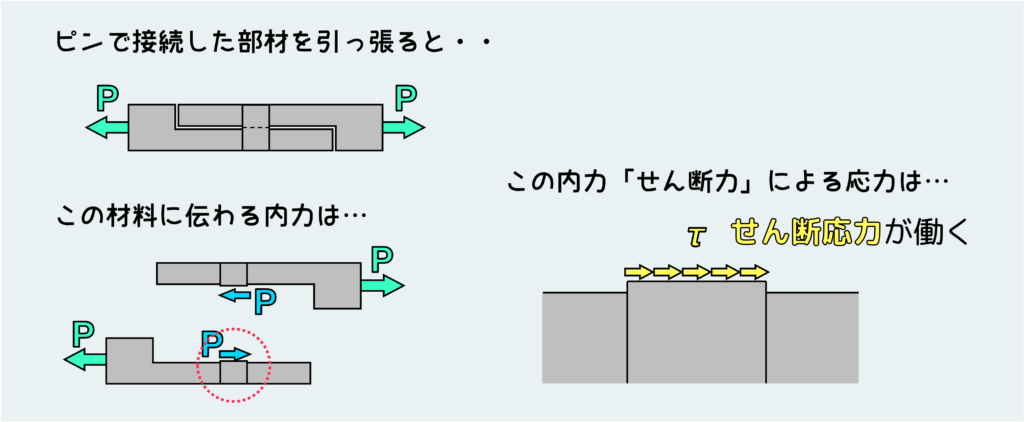
もっと工学的な例を出すとすれば、部材同士を接合するリベットやピンに作用するのもせん断応力だ。
下図のようにピンで接合した構造体を両側に引っ張ると、ピンの断面にはせん断応力が働く。
今回の記事ではこのようなピンやリベットの断面に働くせん断応力について深掘りしていきたい。
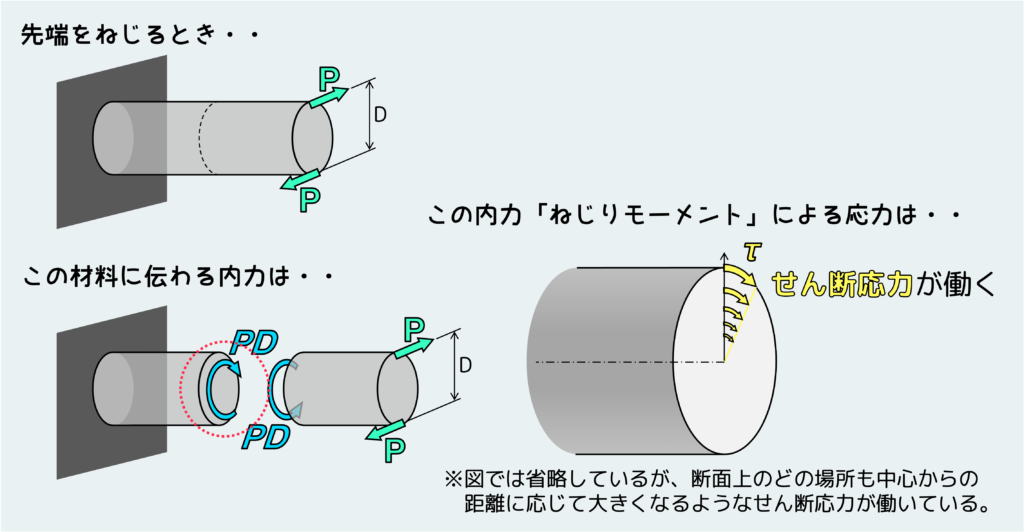
また、せん断応力が登場するもう一つ主要な形態として「ねじり」がある。ねじりを受ける棒の場合、内力として働くのはねじりモーメント（トルク）である。トルクによって発生するせん断応力は「曲げ」のときと同じくある勾配を持った分布となる。つまり「曲げ」のときと考え方は同じで、中心部は変形しないのに対し、表面付近は大きく変形しようとする。そのため、中心部の応力は ”0” であり、中心から離れるに連れて大きくなるようなせん断応力分布となる訳だ。
このようなねじりモーメント（トルク）を受ける材料の応力については別の記事で詳しく説明したいと思う。
ピンやリベットに働くせん断応力
せん断応力は上で説明した通り、面に沿った方向に働く応力な訳だが、ではどの面に働くと考えるべきだろうか？
このことを下の例を元に考えていきたい。
この例では、２つのL字型の板に穴を開け、両者をピンで接続している。これによって２つの板に引張荷重を伝達できるような機構になっている訳だ。分かりやすくするためにカットした3Dモデルも下図に示しているが、ここから先は作図の都合上もう少し簡単なモデル図で考えよう。
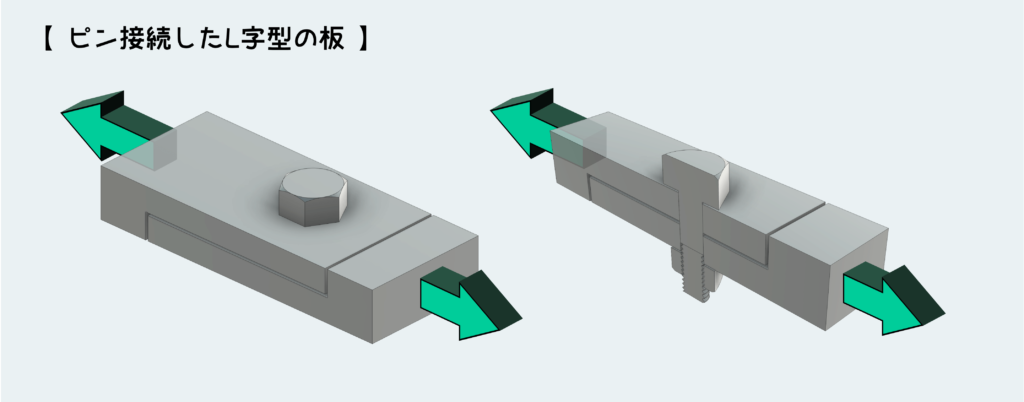
さて、せん断応力の元になっている内力としてのせん断力はどこに働くのか？
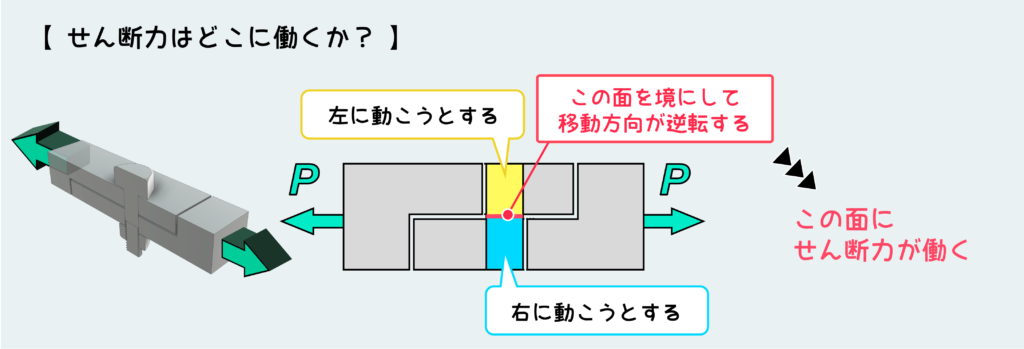
結論としては、『ある面を境にして材料の移動方向が逆転する・かつその移動方向がその面に沿うような方向の場合には、その断面にはせん断力が作用している。』と考えて良い。
文章で書くと分かりにくいので、今回のケースにおいてはどのように考えるべきか図で説明しよう。
今回の例では下図のように、ピンの中央の面を境にして、上半分は左に動こうとするのに対し、下半分は右に動こうとする。しかもこの移動方向は、今考えている中央の面に沿った方向だ。したがって、この中央の面にせん断力が働いていると考えることができる。
（厳密に考えると他の部分にもせん断力は働くが、材力では問題を簡単に考えるために、近似的にピン中央の面のみにせん断力が働くとみなす。そして実際それで実用上十分な精度で考えることができる。）
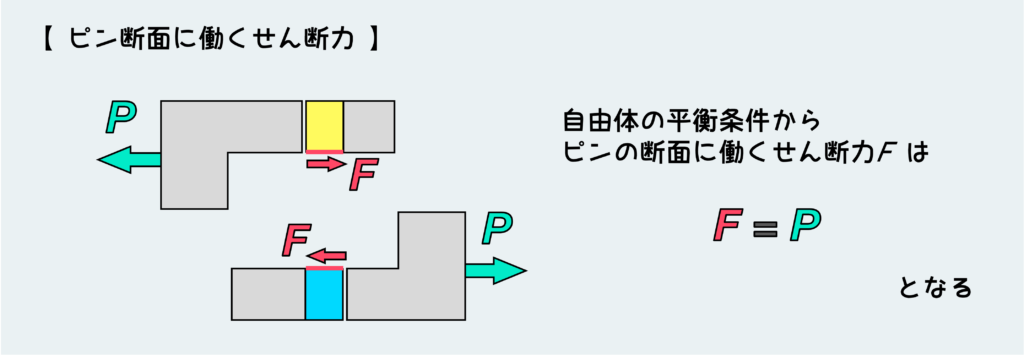
これを踏まえて自由体図を描くと下のようになる。
このせん断力Fは外部から加えている引張荷重とつり合う必要があるので、この場合は、せん断力として外力と同じ大きさのPが働く。（F = P）
このせん断力が作用するピンの自由体の考え方について、下の記事でもう少し詳しく説明しているので、気になる人は合わせて読んでみてほしい。
材料力学《全員必見・超重要》自由体の考え方（異種材料・別部品）【Vol. 1.2-4】
では、このせん断力によって発生するせん断応力の大きさはどのように計算できるだろうか？
ここでも材力お得意の大雑把さが出てくる。厳密にはこの断面内にせん断応力の分布が生じる（つまり場所によって大きさが変化する）はずだが、材力ではそんな難しいことは考えない。
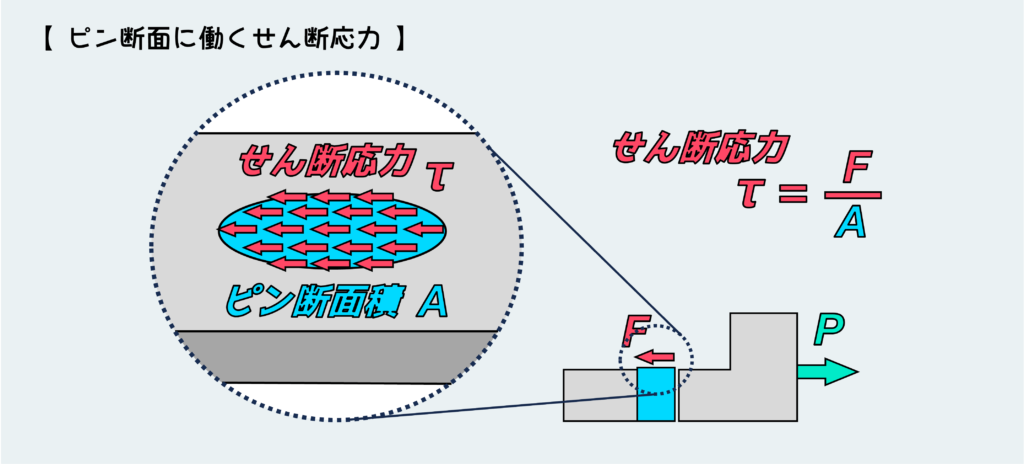
材力では『このせん断力によるせん断応力は断面に一様な大きさで発生する』とみなす。
つまり、発生するせん断応力は断面上のどの位置でも同じ大きさで、その大きさはせん断力を断面積で割ったもので定義される。
これは引張・圧縮問題の時の垂直応力を計算するときと同じ考え方だ。
長々と説明してきたが、大事な点をまとめると要はこういうことだ。
- ある面を境にして材料の移動方向が逆転する・かつその移動方向がその面に沿うような方向の場合には、その断面にはせん断力が作用している。
- このせん断力によるせん断応力は断面上に一様に発生し、その大きさはせん断力をピン等の断面積で割ったもので定義される。
上で説明してきたことをより深く理解するためにいくつかの例を見てみよう。
１つ目は下図のように２つのパイプをピンによって接続しているような状況で、この２つのパイプの両端を引っ張る場合を考えよう。
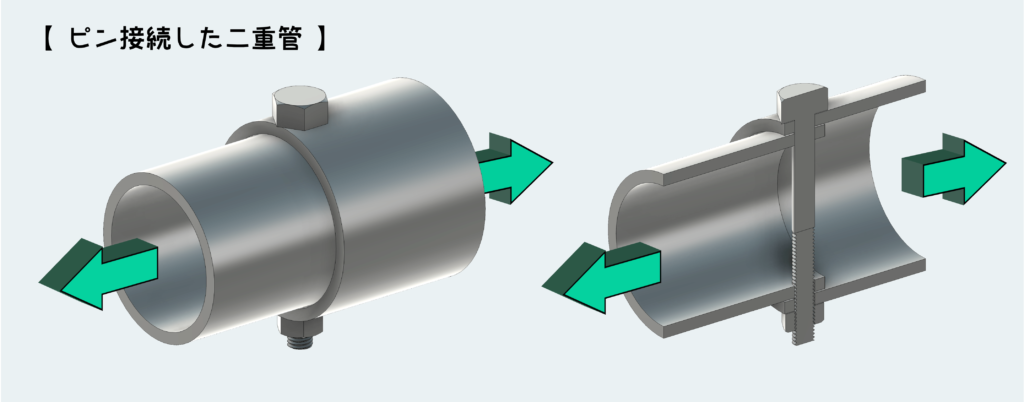
この状況をモデル化して簡単な図にすると下のようになるが、ピンに働くせん断力（内力）やせん断応力を考えるためには、やはり自由体図を描く必要がある。
自由体図を描く際に、どこを仮想的に切断すればいいかと言うと、ピンの移動方向が逆転するような境目の面だ。
すると図のようにピンの上側と下側の部分は右に移動しようとして、中央部分は左方向に動こうとする。この境目の面にせん断力が作用するので、この面で切断した自由体を描くべきだ。
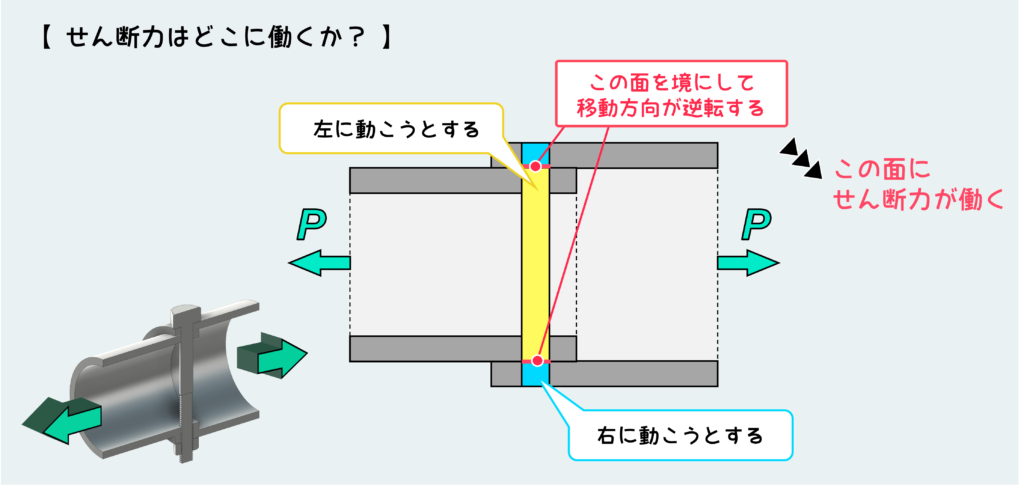
（上の説明でも触れたが、厳密にはせん断力は境目以外の場所にも作用するのでこんな単純な話ではない。しかし、材力の問題として考える上ではこのように大雑把に考えて問題ないし、実際実用上問題ないくらいの精度で応力状態を把握できる。）
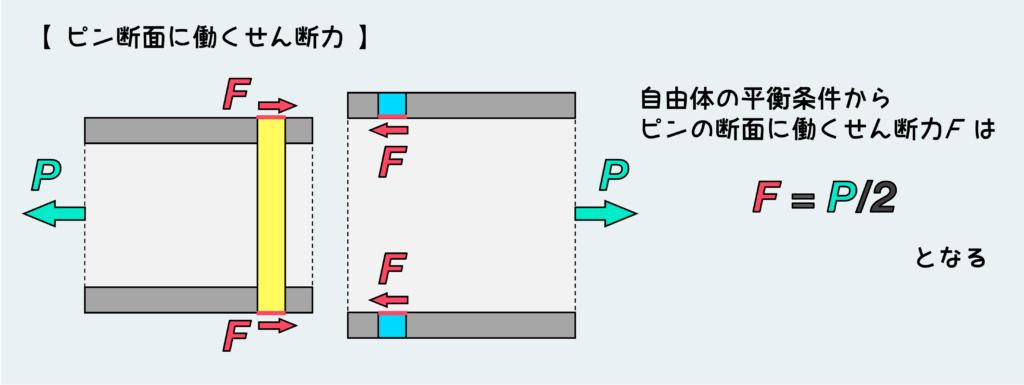
すると、自由体図は下のようになる。この自由体のつり合いからこれらの断面に働くせん断力の大きさを決定する。
上で説明したL字型の板を接続しているときとピンは1本で同じだが、せん断力が働いている面が２つあることが大きな違いである。これによって１つの断面に働くせん断力はF = P/2となる。
ピンに働くせん断応力は、これらのせん断力を断面積で割ればいいので、τ = P/2Aとなる。
このようにピンが1本でも、状況に応じてせん断力が作用する面の数は違うので、当然せん断応力の大きさも状況によって変わる。
大事なことはどの面にせん断力が働くかを見極めることで、そのためには移動方向が逆転する境目の面にせん断力が働くという目を持って問題をみないといけない。
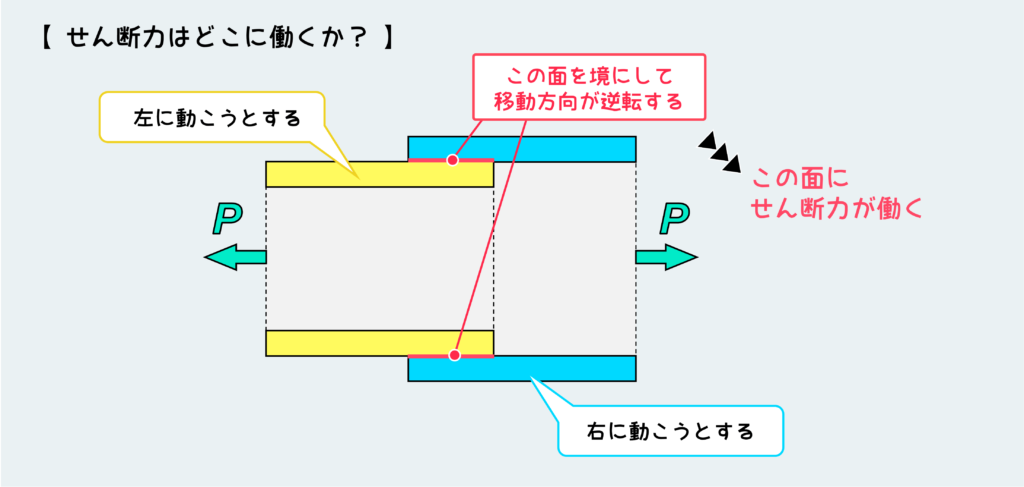
次の例では１つ前の例と同じくパイプが２つ接続されているが、今回はピンによる接続ではなく、パイプ自体を接着している例だ。つまり、「内側のパイプの外面」と「外側のパイプの内面」を接着剤で接着しているような状況だ。
ピンは登場しない訳だが、この場合は接着面自体にせん断力が働く。
原則として、材料が移動しようとする方向がある面を境にして逆転する、かつその移動方向がその面に沿った方向であった場合には、その面にはせん断力が働いている。
この接着面を境にして、外側のパイプは右に動こうとし、内側のパイプは左に動こうとするので、この接着面にせん断力が働いていると考えることができる訳だ。
ではこのとき、この接着面に働くせん断応力の大きさはどうなるだろうか？
まず、接着面に働くせん断力の合計は、自由体のつり合いから外力のPとつり合う必要がある（F=P）。このせん断力が接着面に働くせん断応力を決めているので、せん断応力が知りたればこのせん断力を面積で割ればいい。
このときの面積というのは、このせん断力が働いている面全体のことなので、下のように接着面の面積（内側のパイプの外周 × のり代部の長さ）と考えなくてはならない。
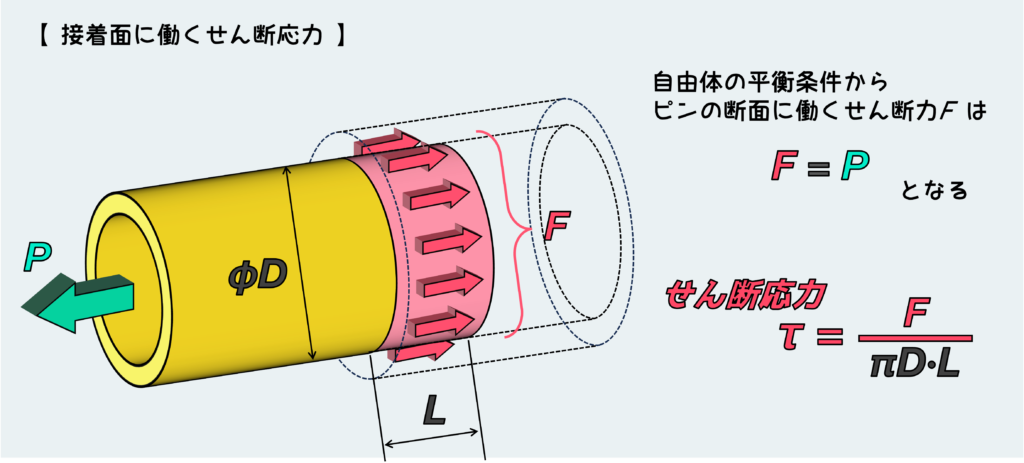
このように、外力とつり合うせん断力がどの面に働いているかを見極めて、そん面積を使ってせん断応力を計算することが大事だ。
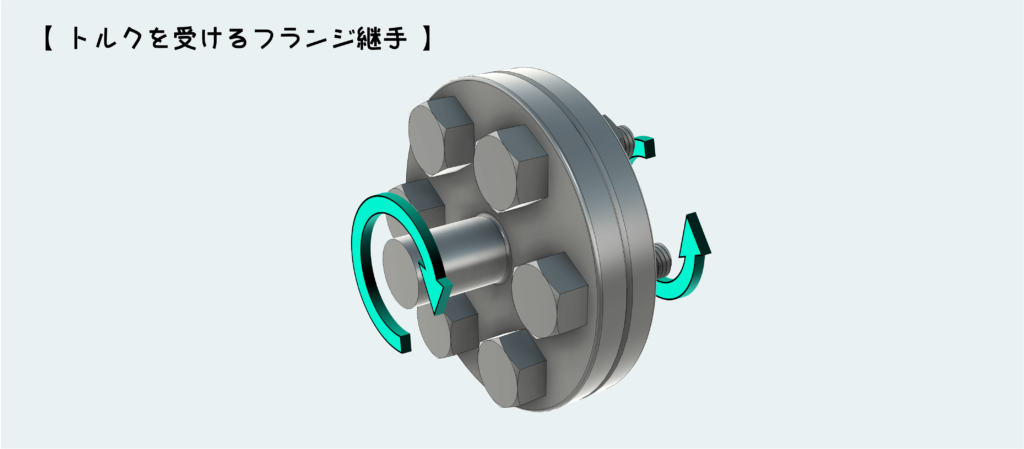
最後の例は、フランジ継手をボルトで接続しているような場合だ。フランジ継手はモーターなどの動力を別の軸に伝達するための部品だ。モーターから伝わってくるトルク（ねじりモーメント）がフランジを介して伝わっていく訳だが、フランジ同士を接続しているボルトにはせん断力が作用することになる。
これをモデル図として描くと、下図のようになる。
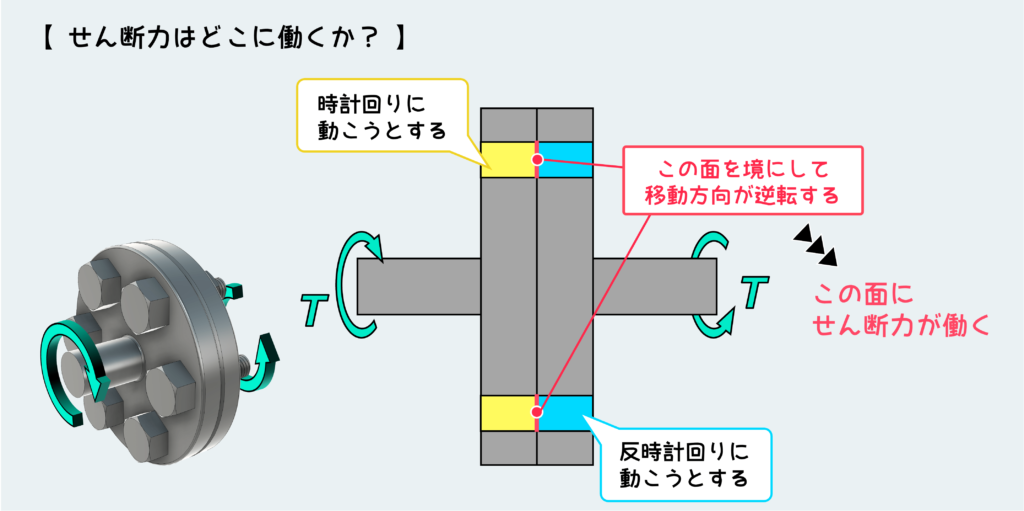
この場合は、手前のフランジが外力のトルクを受けて時計回りに回転しようとしている。一方奥側のフランジは相対的には反時計回りに回転しようとする。そのため、この両者の境目の面にはせん断力が作用することになる。
このフランジ同士の境目の面で仮想的に切断した図を描くと下のようになり、フランジ面同士の摩擦がないとすると、せん断力はボルトの横断面に働くことになる。
これらのせん断力が作る回転モーメントが外力のトルクとつり合う必要がある（回転の平衡条件）ので、フランジ中心を回転の中心としてつり合いの式を立てると（一つのボルト断面に働くせん断力がF、ボルト穴の配置円径がDとする）
\((F\cdot\displaystyle\frac{D}{2}) \cdot 6 = T\)
となる。結局のところ、このせん断力のFをボルトの断面積で割ると、ボルトに作用するせん断応力が求まる。
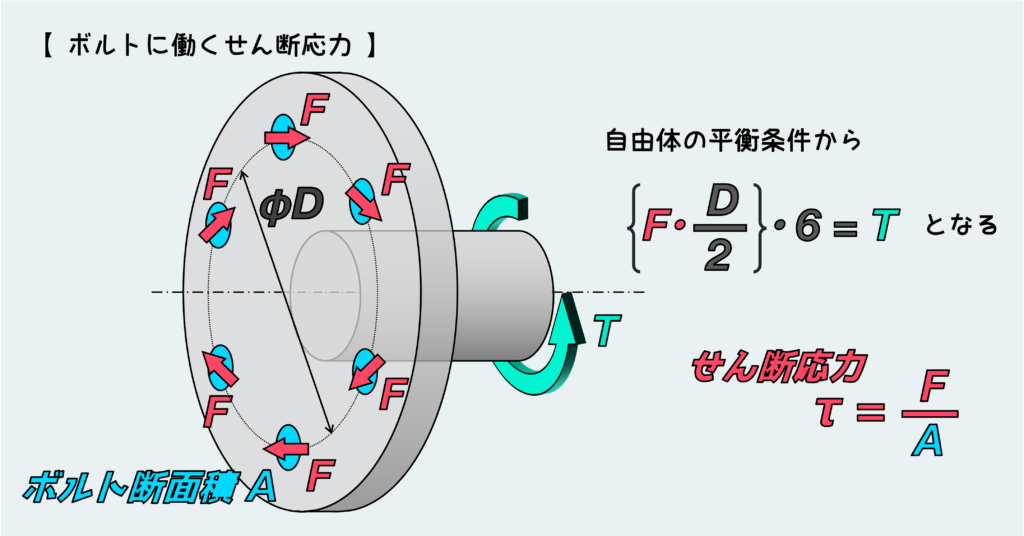
このようにトルクを伝えるボルトやピン接続の場合は、それらに働くせん断力（内力）を見積もるために、回転の平衡条件を考える必要があり、せん断力を伝えるパーツの距離感も重要な要素となる。
内力のせん断力を求めさえすれば、これを各パーツの該当断面積で割ればせん断応力を計算できる。
まとめ
ピンやリベット等に働くせん断応力の考え方について説明してきたが、理解できただろうか？
ポイントは内力としてのせん断力がどこに・どんな大きさで作用するのかを正しく把握することだ。そのためには無論自由体の考え方をマスターしておかないといけない。
内力のせん断力を正しく見積もりさえすれば、これに起因するせん断応力はこのせん断力を断面積で割ることで算出できる。
次の記事からは、せん断応力が問題になるもう一つの主要なケースである『ねじり問題』について説明していきたいと思う。
（記事執筆中）
- せん断応力は、ある面に対してその面に沿うような方向に働く応力であり、ピン等で部材同士を接続している場合や材料にねじり負荷を加えるような場合に問題になる。
- ある面を境にして材料の移動方向が逆転する・かつその移動方向がその面に沿うような方向の場合には、その断面にはせん断力が作用している。
- このせん断力によるせん断応力は断面上に一様に発生し、その大きさはせん断力をピン等の断面積で割ったもので定義される。
