前回の記事では、引張・圧縮の静定問題について説明をしたが、今回は不静定問題についてだ。
 【解き方を誰よりも丁寧に解説】引張・圧縮を受ける材料の静定問題【材力Vol. 3-2】
【解き方を誰よりも丁寧に解説】引張・圧縮を受ける材料の静定問題【材力Vol. 3-2】
不静定問題では、平衡条件に加えて『変形の条件』を考える必要があり、静定問題よりも少し難易度が上がる。
ただ逆に言えば、『変形の条件』さえ正しく導くことができればあとは別に難しくない。少しだけ式をこねくり回す手間が増えるだけだ。
という訳で今回の記事では、『変形の条件』をいかに正しく導くか、ということにフォーカスしながら不静定問題について説明していきたいと思う。
不静定問題が苦手な人は必読の内容だ。
- 不静定問題では、内力の伝わり方を把握するために平衡条件だけではなく、変形の条件を考慮することが必要
- 内力の伝わり方さえ把握できれば、あとは静定問題と同じく応力や変形量を考えることができる
- 変形の条件については、いくつかのパターンを分かっていれば大丈夫!
溢れでる涙を抑えられない!!
全11巻完結
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!
Contents
不静定問題とは?
冒頭でも書いたが、不静定問題とは「内力の伝わり方を把握するために『変形の条件』が必要になるような問題」のことだ。
何度も書いているが、「内力」が材力の問題において非常に重要だ。「内力」がわかることで応力や変形量を考えられるようになる。
静定問題の場合は、必要な場所で材料を仮想切断して、自由体の平衡条件から内力を決定することができた訳だが、不静定問題の場合は加えて『変形の条件』が必要になる。
- 静定問題:平衡条件のみで内力が決定できる
- 不静定問題:内力を決定するためには平衡条件に加えて、変形の条件を考える必要がある
『変形の条件』をうまく使って内力を把握しさえすれば、あとは静定問題と同じで、内力を元に応力や変形量を計算すればいいだけだ。
解き方の流れ
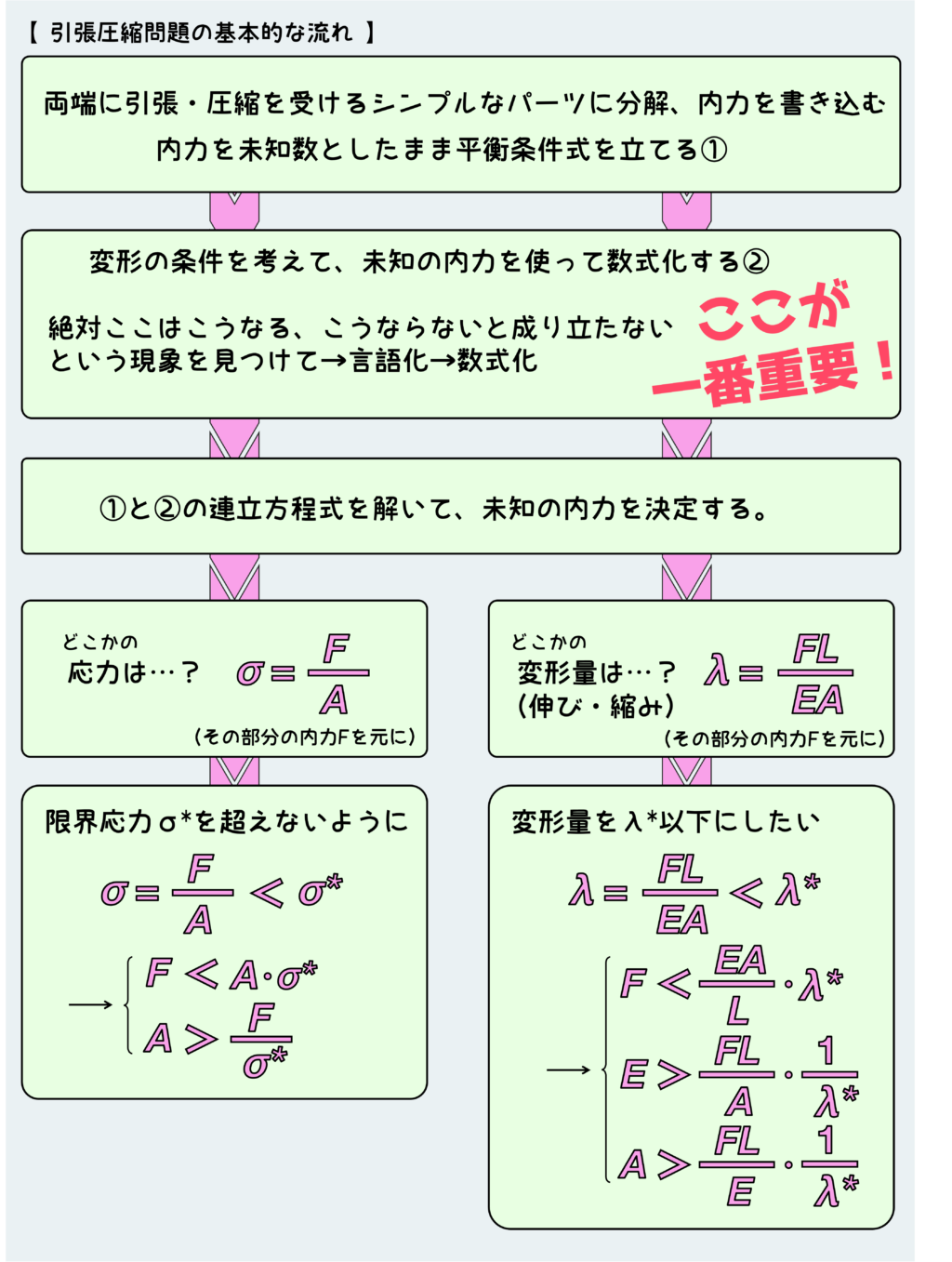
まず、基本の流れを整理しよう。どの問題も流れは同じなので、基本を押さえておけば怖くない。
まずは静定問題と同じく、簡単なパーツに分解して、切断した箇所に内力を書き込んでいく。自由体の平衡条件から式を作る訳だが、静定問題と違って、平衡条件式だけでは内力を決定できないはずだ(未知数に対して式が少ない)。なので、平衡条件式を立てたら、内力は未知数のまま次のステップへ進む。
変形の様子をイメージし『絶対にここはこうならないといけない』という現象を見つける。多くの場合、材料の支点の部分なんかに注目するといい。
『変形の』条件なので、変形量の式\(\lambda=\displaystyle\frac{PL}{EA}\)が必要になる。内力を未知数としたまま必要な部分の変形量を表現し、これを使って変形の条件を数式化する。
ステップ1と2で作った条件式は内力に関する連立方程式になっているはずなので、これを解くことで内力を決定することができる。
内力が求まったらあとは静定問題と同じだ。問われている応力なり変形量なりを、内力をもとに計算すればよい。
例題を解いて、解き方を身につけよう
では2つの問題を解いて、解く流れを身につけよう。
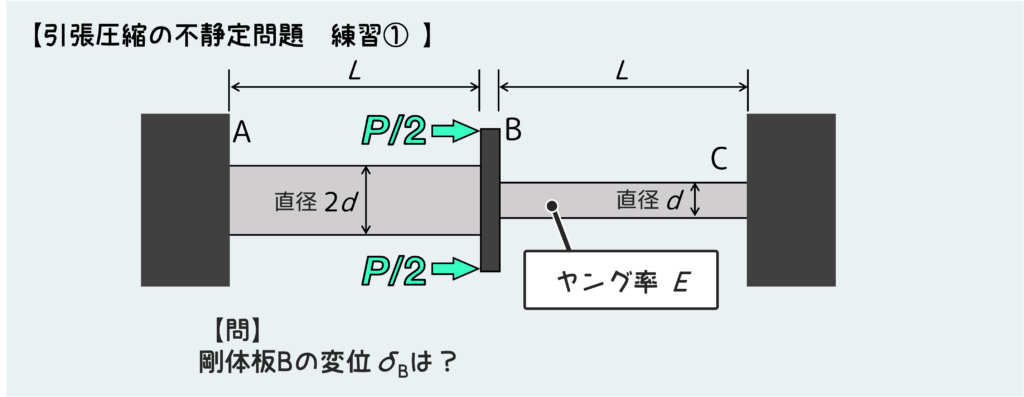
まずは下図のような問題だ。
2つの棒が剛体棒を介して接続されており、その両端が壁で固定されている。このどちらかの壁が存在せず自由端になっていたら静定問題だが、両端をはさまれることで不静定問題になってしまう。
これが超基本の不静定問題だ。
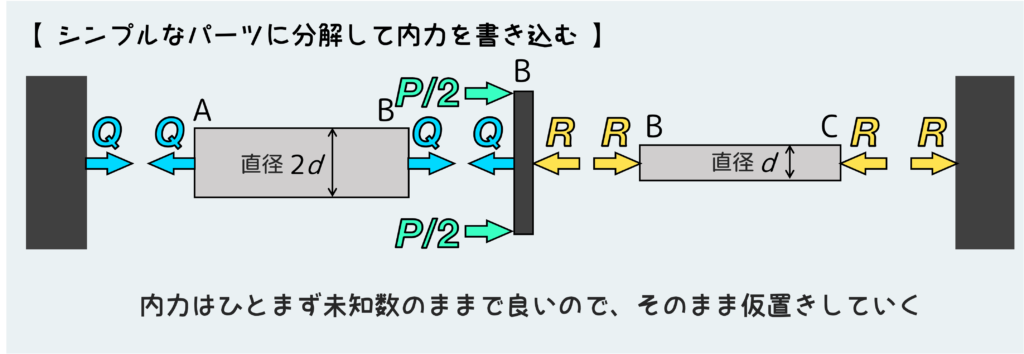
まずはシンプルなパーツに分解して、これらに働く内力を書き込んでいく。
この問題の場合は、中央の剛体板を右向きに押しているので、左の棒ABには引張が、右の棒BCには圧縮がかかることが想定できる。
まあここの仮置きが間違っていたとしても、別に問題ないので安心してほしい。もし間違っていた場合は最終的な答えがマイナスで出てくるので、そうしたら最初の仮置きが間違っていたんだなと気付ける。
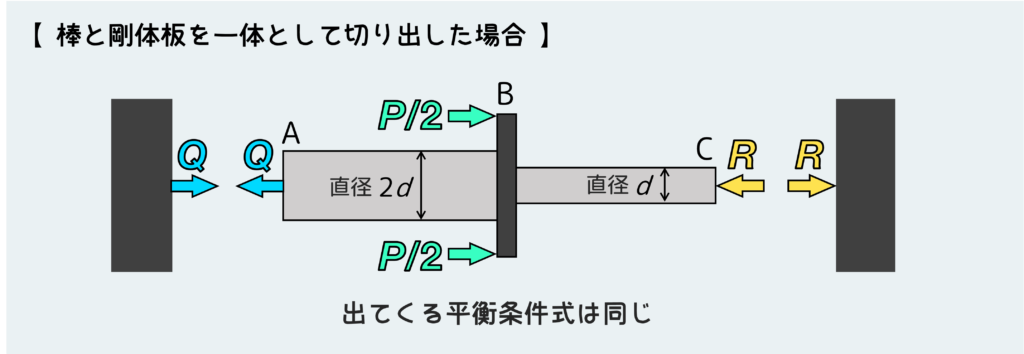
棒AB、BCと剛体板を分解せずに自由体とすることももちろんできる。
下図のようになる訳だが、やってみれば分かるが導き出される平衡条件式の内容は上図のときと変わらない。
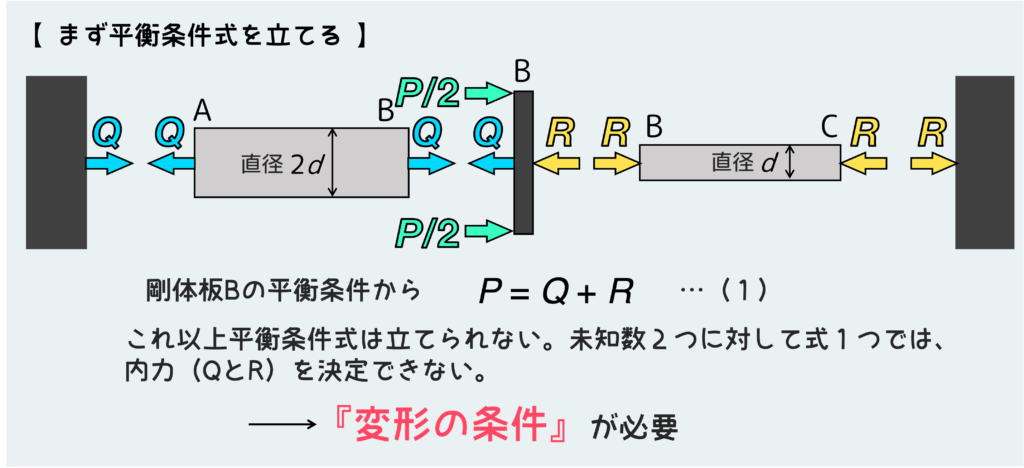
自由体図から剛体板Bの平衡条件を考えて、式を立てる。出てくる式はP=Q+Rとなり、これ以外に条件式は出てこないので、これでは未知の内力QとRを決定できない。未知数が2つあるので、もう1つ条件式が必要だ。
という訳で、変形の条件が必要になる。こういう問題が不静定問題という訳だ。
さて変形の条件を見つけるにはどうしたらいいだろう。最初はやはり変形の様子をイメージすることが一番いいと思う。そしてイメージができたら、いくつかのパターンを知ることだ。
『こういうときは条件としてはこれ』というパターンがいくつかあり、それさえ理解してしまえばほとんどの問題に対応できると思う。
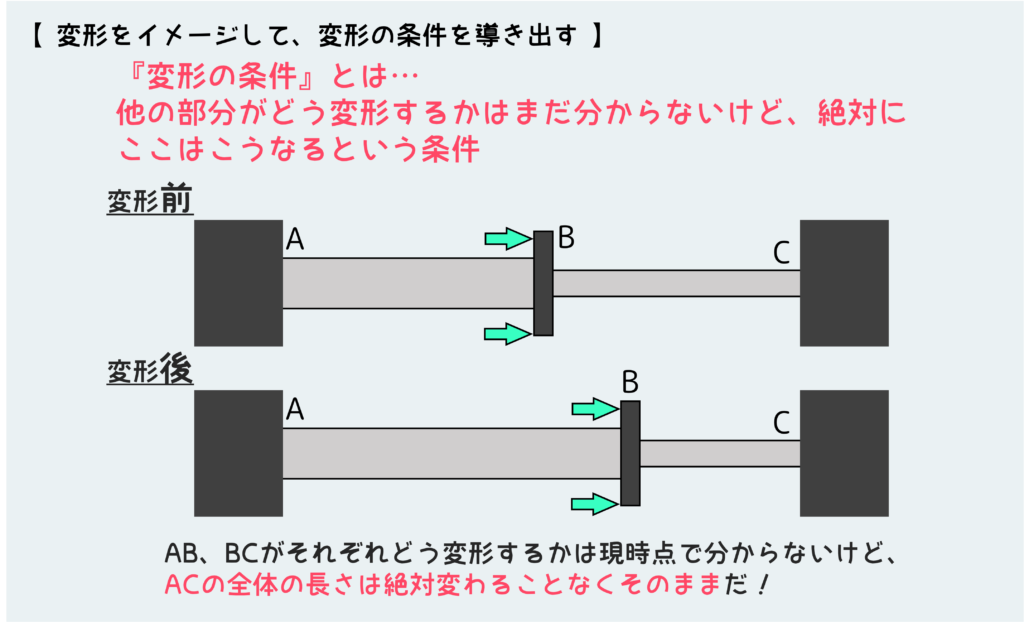
では今回の問題ではどうだろうか。変形の様子をイメージすると下のようになる。
コツは『他の部分がどうなるかはまだ分からないけど、絶対にここはこうなる』というポイントを見つけることだ。
今回は両端を壁で『固定』しているので、絶対こうなるというポイントは『AからCまでの全体の長さは絶対変わることなくそのまま』ということだ。
これが上で言ったようなひとつのパターンで、引張圧縮問題で両端固定の場合は決まってこの条件になると言ってもいい。
条件が見つかったらこれを数式化する必要がある。
変形の条件なので、長さが不変といってもそれは「変形しない」という意味ではない。もう一度変形の様子をよくイメージしよう。すると、これをどう表現すればよいか。。
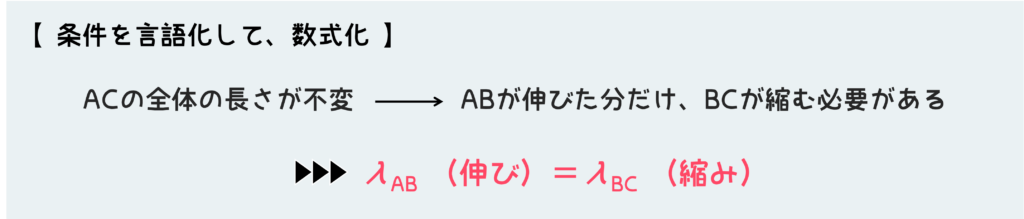
全体の長さが不変ということは、「ABが伸びた分だけ、BCが縮む必要がある」と言い換えることができるだろう。
ということはつまり、ABの伸びλABがBCの縮みλBCに等しいということである。
ここまで来たら変形量の式を使って、変形の条件を式化していく。
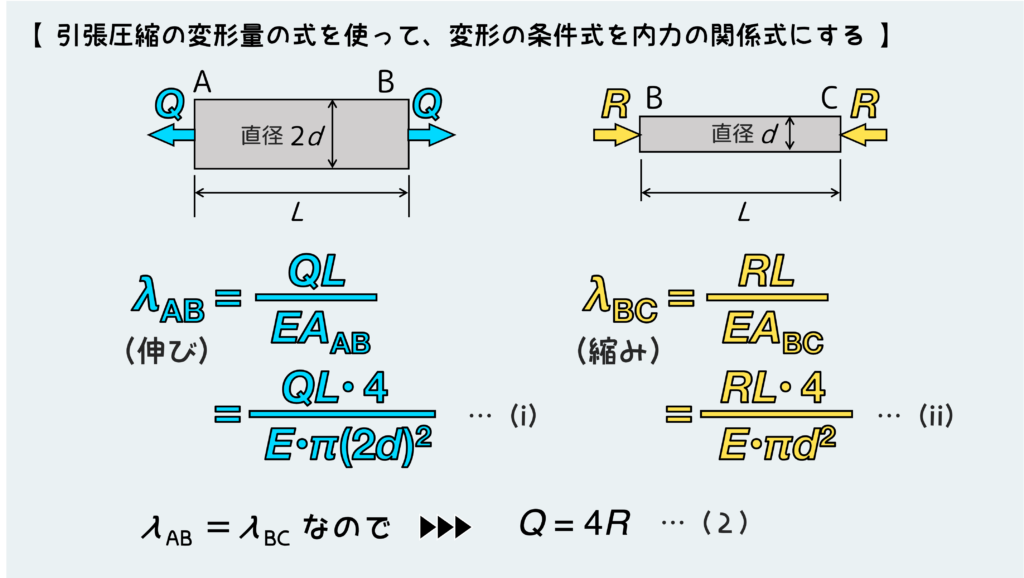
ABには両端にQが働き、BCには両端にRが働くという風に内力を仮置きしていたのだから、この未知の内力を使ってAB、BCの変形量(伸びと縮み)は下のように表現できる。
これらが等しいというのが変形の条件なので、これをイコールで結べば足りなかったもう1つの内力の関係式を得ることができる。
平衡条件式(1)と変形の条件から得られた関係式(2)が揃ったので、これらの連立方程式を解けば、内力QとRを求めることができる訳だ。
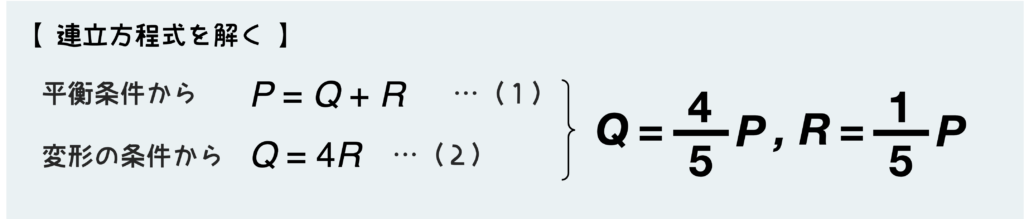
さて、内力さえ決定できればあとは静定問題となにも変わらない。内力をもとに然るべき応力や変形量を計算していけばいいだけだ。
今回問われているのは剛体板Bの変位、つまり剛体板が外力によってどれだけ右に動くのか?ということである。
これは言い換えれば、ABがどれだけ伸びるか?ということでもあり、BCがどれだけ縮むのか?ということでもある。
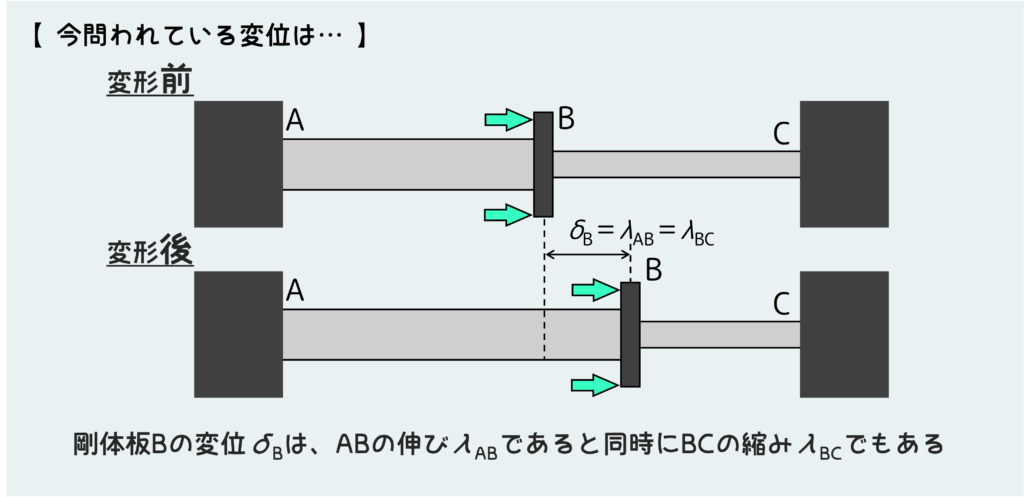
ABの伸びとBCの縮みについては、変形の条件を考えるときにすでに考えたはずだ。
ただし、あのときは内力QとRが未知の状態で式を作っていた。でも今はQとRがすでにわかっている。
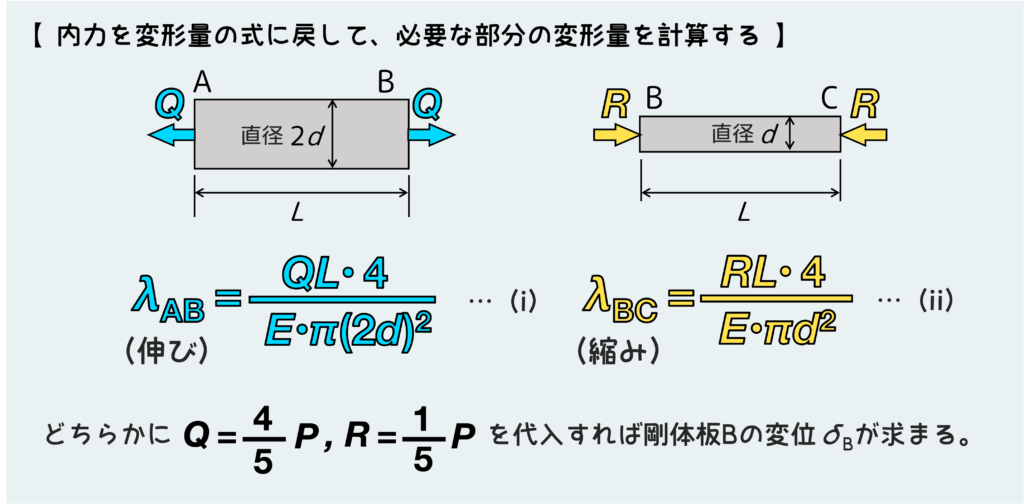
変形の条件を考える時に使った式に、求めた内力QとRを代入すれば、具体的にABの伸びおよびBCの縮みを計算できる。
まあ実際ABの伸びもBCの縮みも同じ(そういう変形の条件だったよね)なので、どちらか一方の式を使えば十分だ。
基本を身につける意味でめちゃくちゃ丁寧に説明してきたが、いかがだろうか。
実際はこんな時間をかける必要はない問題だが、丁寧に読んでくれた人は流れがよく分かったのではないだろうか。
この基本の流れは他の不静定問題でも同じなので、ぜひよく理解してほしい。
ではもう1つだけ例題を解いてみよう。次の問題では、変形の条件がさきほどの問題とは違うパターンになる。
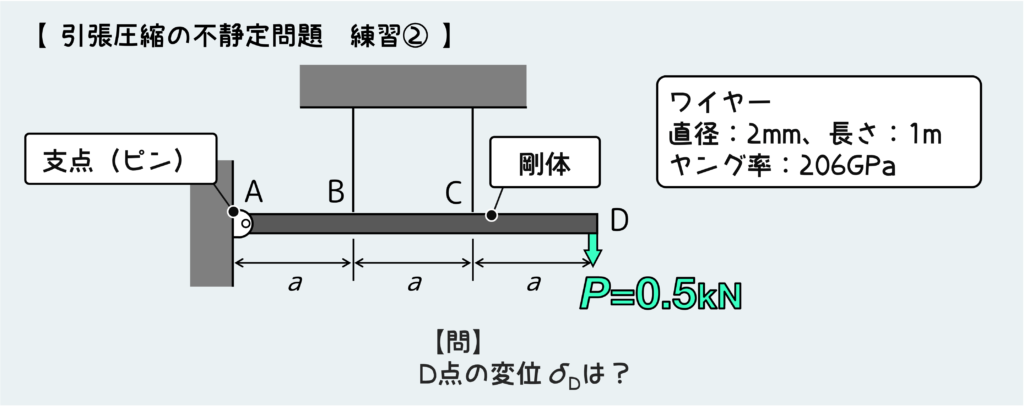
下図のような問題だ。
壁Aでピン支持された剛体棒がBとCのところでワイヤーで吊っており、先端Dに荷重0.5kNが作用している。このとき先端D点の変位を考えよう。
まずはシンプルなパーツに分解して、書き込める内力を確実に書き込んでいこう。
どんな問題もここから始まると言ってもいいぐらい、このプロセスは基本であり重要だ。『自由体なんて書かなくても大丈夫っしょ』という人に限ってテストの点数は悪かったりするものである。
素直に毎回自由体を描いてから問題を解くようにしよう。
ここでのポイントはA点の支持方法だ。ピン支持なので、モーメントを支えることはできない。なので、Aのところに書き込める内力は上下方向の力と左右方向の力のみでモーメントは書き込めない。(左右方向の力は他に発生する場所がないので、結果的に左右方向の力も書き込まなくていい)
支持方法によって自由体に書き込める内力が変わる話は、以下の記事でまとめているのでぜひ合わせて読んでみてほしい。
 材料力学《全員必見・超重要》自由体の考え方(色んな支持方法)【Vol. 1.2-2】
材料力学《全員必見・超重要》自由体の考え方(色んな支持方法)【Vol. 1.2-2】
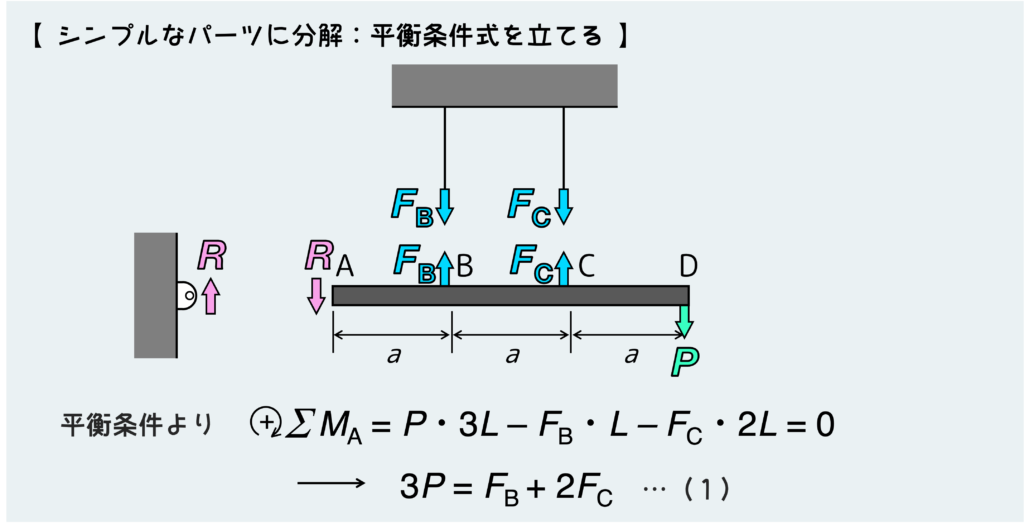
出来上がった自由体図を元に平衡条件式を立てると、下のようになる。
これも未知数2つに対して、この式1つしかできないのでこのままでは解けない。つまり不静定問題だ。
いや、ちょっと待てよ。上下方向の釣り合いの式を立てれるでしょ?、、と思った人もいるだろう。たしかにそうだ。
でもこれは意味がない。上下方向の釣り合いの式を作っても、支点Aのところで壁から受ける反力Rが新たに式に加わるので、式が1つ増えるけど未知数も1つ増えることになり足しにならないのである。
結局は変形の条件を考える他にないのである。
(今回は反力Rについて問われていないので、上下方向の釣り合い式を作っていないが、これが問われるような場合にはもちろん必要になる。)
さて、では今回の変形の条件は何だろうか。例によってイメージしてみるのが大事だ。
変形後の状態は下図のようになる訳だが、今回のポイントはADが剛体であるということだ。
これが剛体であるおかげで、ワイヤーBとワイヤーCの変形の間に非常に簡単な関係性を見出すことができる。
つまり、下図において三角形ABB’と三角形ACC’の間には相似の関係があり、このことからBの伸びλBとCの伸びλCのの間には2λB=λCの関係がある、ということが分かる。
これがこの問題の変形の条件だ。

この事に気が付いたら、あとは例題①のときと同様に、未知の内力を使ってこの関係式を表現してやればいい。
今、それぞれのワイヤーには引張の内力FBとFCが働いていると仮置きしているので、変形の条件は下のように表現できることになる。

これで平衡条件式と変形の条件式の2つが出揃った。未知の内力2つに対して式が2つあるので、連立方程式を解けばそれぞれの内力を決定することができる。
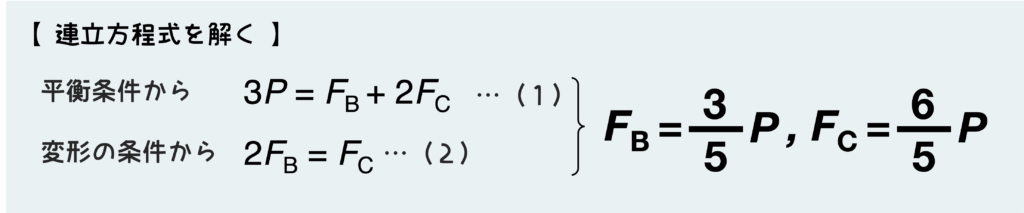
さて内力を決定することができたら、あとは今問われているものをもう一度確認しておこう。
この問題で問われているのは先端D点の変位だ。もう一度、変形の条件を考えた時と同様に変形後の様子を確認してみよう。
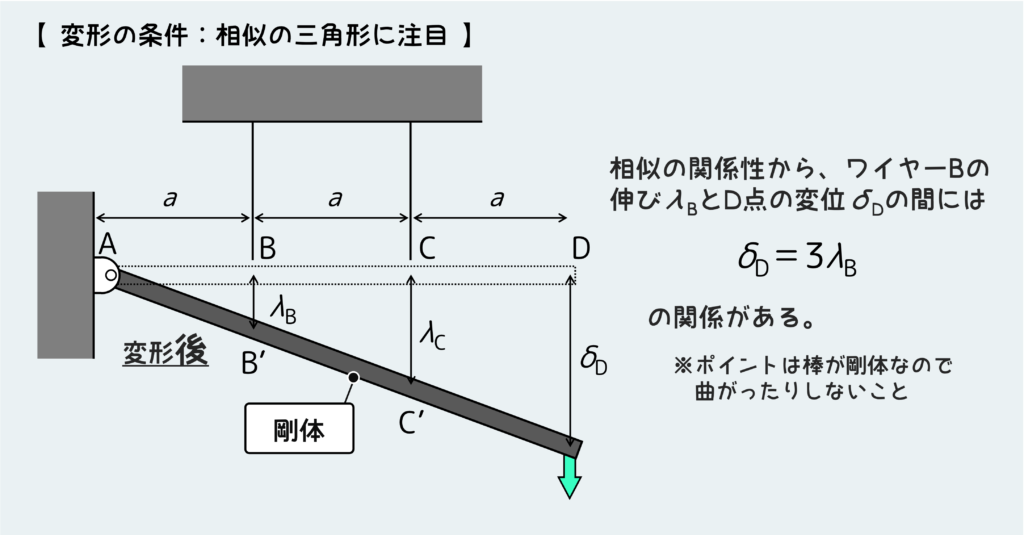
そうすると下図のように、やっぱり相似の三角形があることに気付けると思う。
この相似関係を利用して、今求めたい変位δDとワイヤーBの伸びλBの間にはδD=3λBという関係があることが分かる。これを利用すればδDを計算することができるだろう。
さてワイヤーBの伸びλBの計算には、さきほど求めた内力FBを入れればいい。
文字式で答えを出すような問題ならここで終了だが、数値を入れて計算するような問題の場合はここからさらに計算が続く。そのときには絶対に単位に注意を払おう。
単位計算をする際には、数式の中に数値を入れていくときに『長さ系は(mm)、力は(N)、応力やヤング率は(MPa)に直してから入れる』のがコツだ。
そうすると下図のように計算を進めることができる。(MPa)=(N/mm2)なので、うまいこと単位が消しあってくれて、この問題の場合は残る単位が(mm)なので、出てきた計算結果に(mm)を付ければ正しい答えが手に入る。
計算における単位の考え方とそのコツについては、以下の記事をぜひ読んでみてほしい。
 材料力学 公式を正しく使い、計算ミスを減らすコツ【材力 Vol. 0.3】
材料力学 公式を正しく使い、計算ミスを減らすコツ【材力 Vol. 0.3】

まとめ
不静定問題、、苦手な人もいるのではなかろうか。
でも今回まとめてみて改めて感じたが、決して難しくはない。
ポイントは変形の条件だ。これの考え方とパターンの理解さえできれば、あとはもう何も怖くない。いつになるか分からないが、いつか変形の条件パターン集みたいな記事もまとめていきたいと思う。
次の記事では、トラス構造について説明していきたいと思う。これも苦手な人がたくさんいると思うので、ぜひ読んでみてほしい。
- 不静定問題では、内力の伝わり方を把握するために平衡条件だけではなく、変形の条件を考慮することが必要
- 内力の伝わり方さえ把握できれば、あとは静定問題と同じく応力や変形量を考えることができる
- 変形の条件については、いくつかのパターンを分かっていれば大丈夫!
溢れでる涙を抑えられない!!
全11巻完結
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!





