材料力学　【解き方を誰よりも丁寧に解説】引張・圧縮を受ける材料の静定問題【材力Vol. 3-2】

材料力学の問題には、静定問題と不静定問題の２種類がある。

不静定問題の方が問題を解くために考えることが１つ多いため、やや難しくなる。今回の記事ではまず静定問題、特に引張・圧縮の問題の解き方について説明していく。

あらゆる問題に通じる内容なので、ぜひ最後まで読んでみてほしい。

静定問題とは？

冒頭でも書いた通り、材料力学には静定問題と不静定問題の２種類がある訳だが、両者の違いとは何だろうか？

一言で言うと『問題を解くために変形の条件が必要か否か』だ。

どんな問題も材料に伝わる内力を把握することから始まる訳だが、内力を考えるためには材料を自由体として仮想的に切断して、これに平衡条件を適用して内力を求めていく。これが静定問題の流れだ。

しかし、拘束条件がひとつ多かったりすると不静定問題へと変化し、これの内力を決定するためには平衡条件だけでは足りずに、『変形の条件』も加味して考えないといけなくなる。つまり、

言わずもがな、不静定問題の方が考えることが多いので難しい。

この記事ではまず基本の静定問題の解き方をしっかり押さえていこう。ここがしっかりしていないと、不静定問題ではさらに苦労することになる。

解き方の流れ

何が問われる？

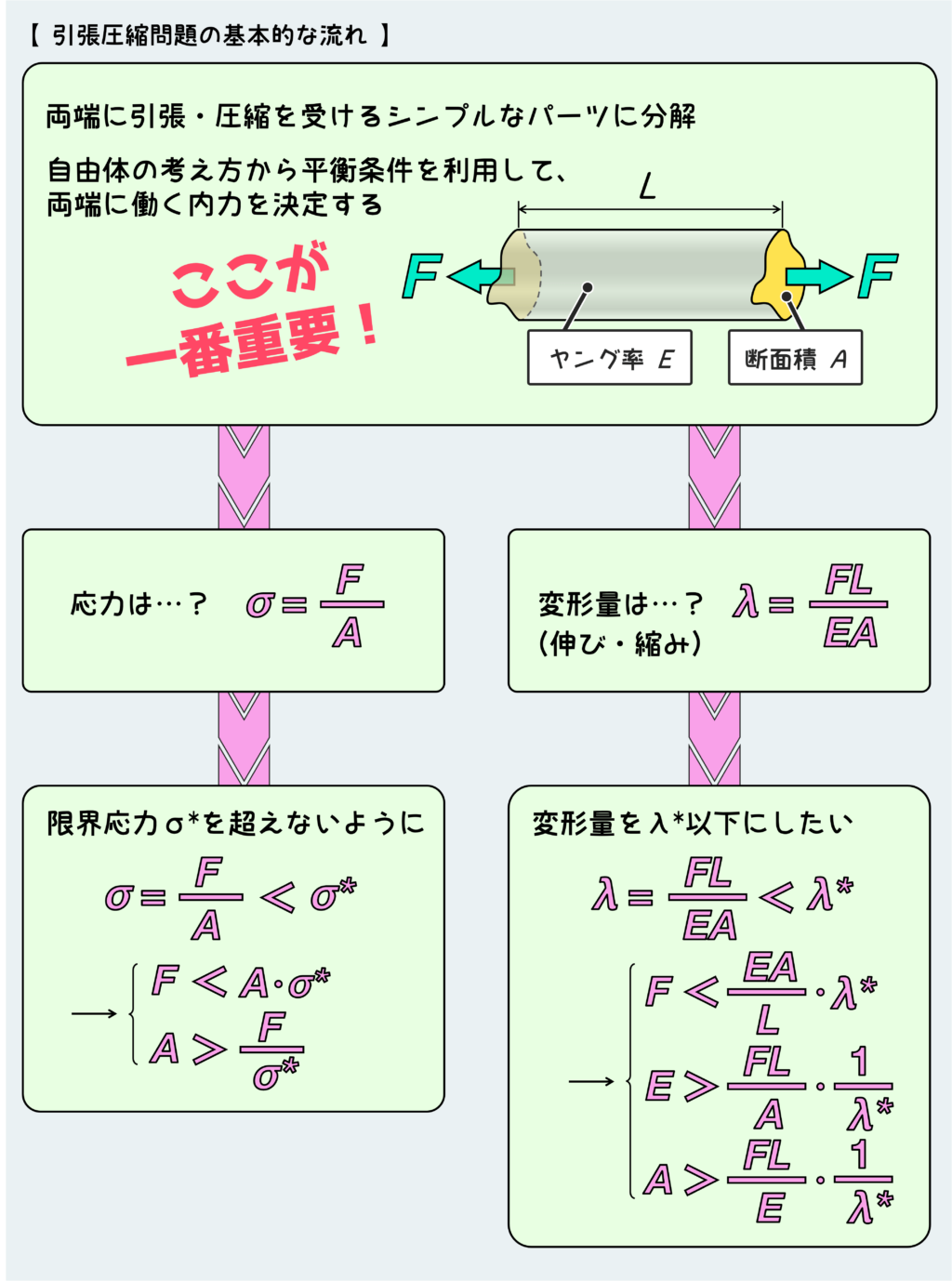
たいがいの問題において、問われるのは応力か変形量だと思われる。これらは割とシンプルな問題で、与えられた材料の条件や外力を元にして、応力や変形量を求めていけばよい。

あと考えられる問題としては、応力や変形量に制限を付けて（応力を○○MPa以下にしたい、など）、それを実現するためには外力や寸法や材質をどうすればいいでしょう？というような問題だろう。

いずれにしても未知数となるものの種類が変わるだけで、使う関係式は同じで１つか２つしかないので、以下の基本の解き方をしっかり押さえれば何も問題はない。

基本的な解き方

ではここから、基本的な解き方について丁寧に説明していきたい。

例題を解いて、解き方を身につけよう

例題１

では簡単な例題を解く流れを確認して、基本的な解き方をしっかり理解しよう。

まず下図のような問題を解いてみよう。直径の異なる丸棒が接続されていて、先端のC点に外力Pが作用している。このときの丸棒AB、BCに発生する引張方向の応力と、先端C点の変位（動く距離）を知りたい。

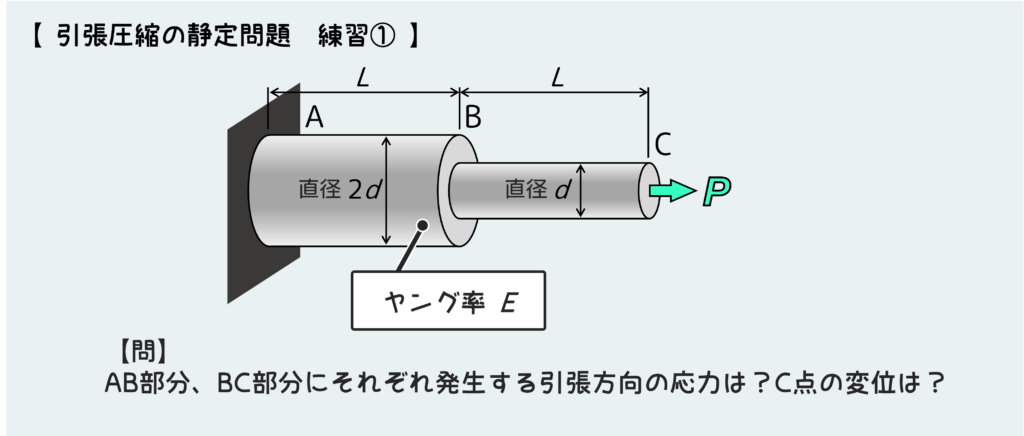
まあ普通に考えてAB部とBC部に分解するのが正解だ。AB部とBC部に発生する応力を知りたければ、これに働く内力を知る必要があるので、それぞれバラバラのパーツにして、内力の伝わり方を把握しないといけない。

各部分を分解して、内力を書き込み、平衡条件と作用・反作用の法則からその大きさを決定していくと下図のようになる。

図中の番号①〜④は思考の順番だ。分解した後やみくもに平衡条件を使おうとしても上手くいかない。セオリーとしては外力が作用しているところから攻めていくことだ。

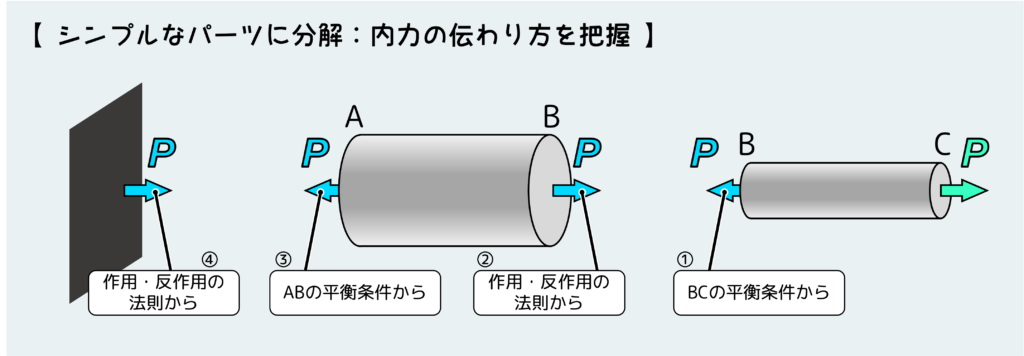
ここまで分かれば、あとは応力や変形量の関係式に文字や数値を入れていけばいいだけだ。

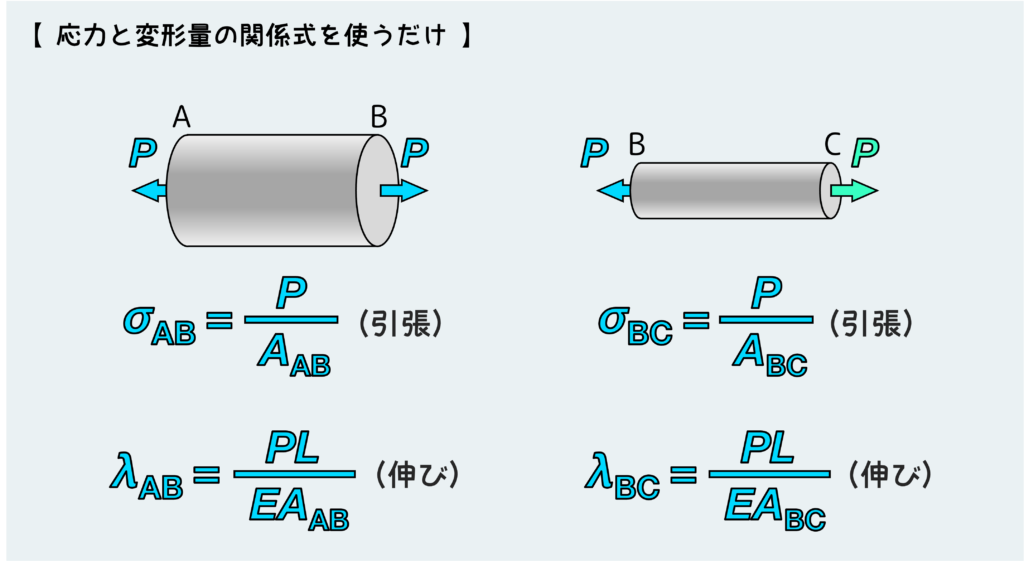
この問題ではAB部もBC部も引張力Pが作用している丸棒なので、それぞれの応力と変形量は下のようになる。

ABは直径2d、BCは直径dなので、応力はそれぞれ\(\sigma_{AB}=\displaystyle\frac{P}{\pi(2d)^2/4}\)、\(\sigma_{BC}=\displaystyle\frac{P}{\pi d^2/4}\)となる。

変形量（伸び）についても同様に下図の式にそれぞれの断面積を入れていけば良い。

今回の問題では数値は与えられていないので、ここで終わりだが、数値を扱う場合は単位に注意を払うことを忘れないようにしよう。

最後に全体の変形について考えて、C点の変位を求める。

この構造全体は下図のように、AB部の伸びとBC部の伸びが合わさって変形するので、C点の変位は\(\delta_C=\lambda_{AB}+\lambda_{BC}\)となる。

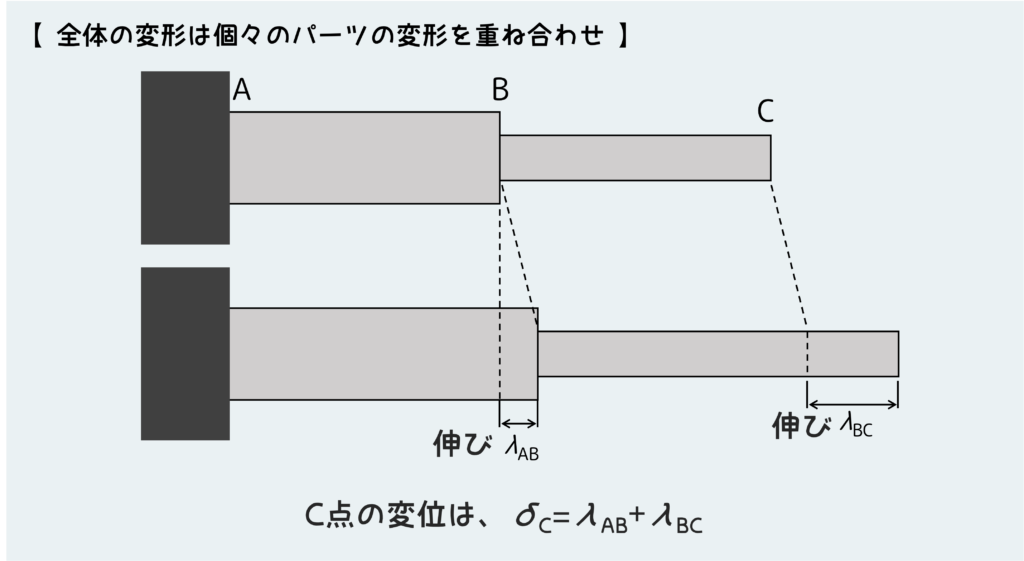
今回はどちらも引張なので、そこまで混乱することはないが圧縮がまざるときは少しだけ慎重になった方がいい。

個人的には、絶対値で計算するのが間違いがないように感じる。仮に、引張力Pを受ける材料と圧縮力Pを受ける材料があるときに、どちらも大きさだけを考えて”P”として公式に入れていく。その結果、応力や変形量も（引張応力だろうが圧縮応力だろうが、伸びだろうが縮みだろうが）正の値として導かれる。全体の変形量を考える時はこれらを正しく足したり引いたりして計算しないといけない。

もしくは、引張・伸びを『正』、圧縮・縮みを『負』と決めて計算していくやり方もある。この場合、全体の変形量を考えるときは単純に計算結果を足し合わせていくことになる。伸びは『正』、縮みは『負』として足し合わせていく訳だ。

正直、この辺は好みと慣れの問題なので、正しい結論に辿り着けるならどちらの考え方でもいいと思う。

例題２

では２つ目を解いてみよう。今度はワイヤーが剛体をつっている問題で、このワイヤーの限界強度が与えられており、ワイヤーが破損しない限界の荷重Pを問われている。

まずACが剛体だということをちゃんと認識したい。これが剛体じゃなかったりすると全く違う問題になってしまう（荷重PによるACの曲げを考慮しないといけなくなる）。

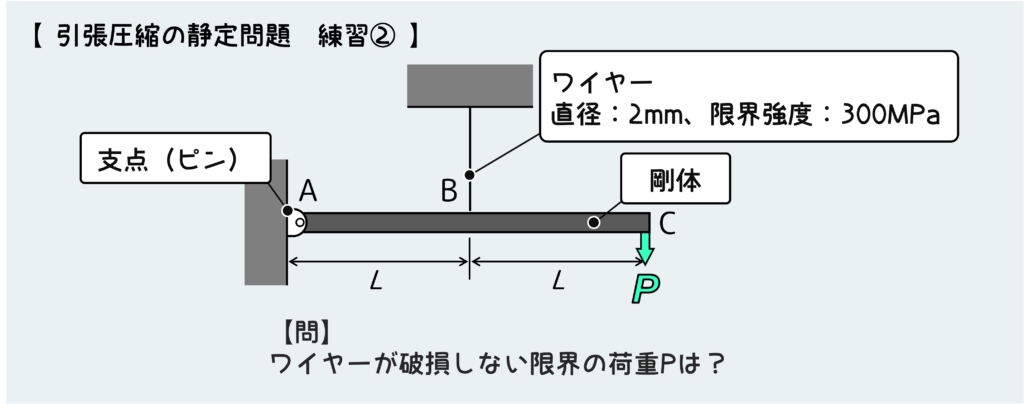
ワイヤーにかかる応力を知りたいので、ワイヤーと剛体ACを分解しないといけない。剛体の平衡条件しか突破口がないのでもちろんこれを考える訳だが、注意しないといけないのは未知の内力の書き込み方だ。

仮想的に切断した箇所に内力を書き込んでいくのだが、適当に書き込んではいけない。その箇所に書き込むべき内力と書き込んではダメな内力がある。

たとえばこの問題の左端はピン支持されているのだが、この支持方法によっても書き込める内力は変わる。ピン支持はモーメントを支えることができないので、この問題では左端のAのところに内力としてモーメントを書き込んではいけない。

またワイヤーや細い紐のように表現されるものは、そのワイヤーの長手方向に働く引張力のみを支えられると考えるのが一般的だ。つまりこの問題では、ワイヤーの下端のところに書き込めるのは下方向の力（ワイヤーにとって引張）だけで、せん断力（左右方向の力）やモーメントを書き込むことはできない。

支持方法や接続方法によって自由体図に書き込める内力が変わる話については、以下の記事に詳しくまとめているのでぜひ読んでみてほしい。

材料力学《全員必見・超重要》自由体の考え方（色んな支持方法）【Vol. 1.2-2】

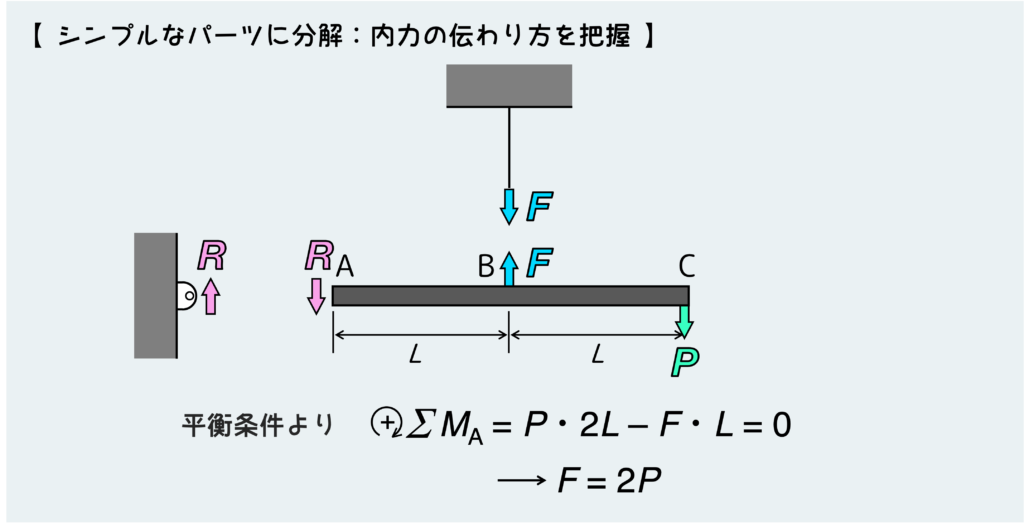
という訳で、正しく内力を書き込めれば、あとは平衡条件から簡単にワイヤーに働く引張力F=2Pだと分かる。

これを元にワイヤーに働く応力が計算できる訳だが、今回の問題では限界強度が与えられているので、この応力と限界強度を不等式でつなげることになる。

今回は外力のPが問われているので、これを未知数のまま式を立てて、限界強度の300MPaと比較する訳だ（不等式を解く）。すると下のように、ワイヤーが破損しない（つまり応力が限界強度の300MPaを超えない）ような外力Pの条件が求まる。

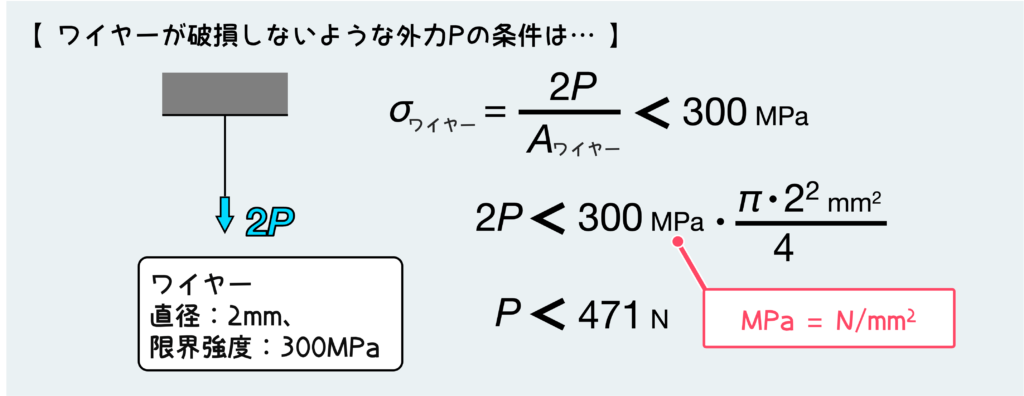
このように具体的な数値を与えられて計算するときには、単位にはめちゃくちゃ注意を払ってほしい。計算自体が間違ってなくても、単位換算に間違いがあれば何も意味がない。ペーパーテストで点数を失うだけならまだマシだが、最悪命にかかわるような事故につながってしまうので、単位のことは絶対にしっかりと理解する必要がある。

材力で出てくる単位計算のコツは以下の記事で説明しているので、よく分からずにいつも問題を解いているような人はぜひ一度目を通してみてほしい。

材料力学　公式を正しく使い、計算ミスを減らすコツ【材力 Vol. 0.3】

まとめ

まず簡単な引張・圧縮の静定問題について説明してきたが、いかがだろうか。

今回の内容が多くの問題の基本形と言っても良い。曲げやねじりと負荷形態が変わっても大きな流れは変わらず、使う式が少し変わる程度だ。

ぜひ今回の内容をしっかりと押さえて、発展的な問題も解けるようになろう。

次回は引張・圧縮の不静定問題について整理していこうと思うので、そちらも読んでみてほしい。