「θが十分小さいとき、sinθ ≒ θ とみなされるので……」のような解説の文章を読んだことがある人もきっと多いと思う。そして、多くの人はこう思っただろう。
なんで!?
もうこれはいわゆる初見殺しみたいなもので、初めて遭遇した人が「どういうこと?」と疑問を抱くのは当然だ(なにも疑問に思わずスルーしてしまうのは、それはそれで問題だ)。
sinθ というのは、「直角三角形の斜辺と縦の辺の長さの比」だし、θ は当然「角度」のことだ。この2つをなぜほぼ同じだと言えるのだろうか?
この近似は、材力だけでなく、多くの理工学系の学問で登場する。今回は、なぜこんな近似ができるのか、その考え方を説明したい。
角度の単位(rad)についていまいち理解できていないという人は合わせて以下の記事も読んでもらえると、理解がしやすいと思う。
 角度の単位(rad:ラジアン)とは?(°:度)やdegへの変換は?【番外1】
角度の単位(rad:ラジアン)とは?(°:度)やdegへの変換は?【番外1】
- sinθは、斜辺の長さが “1” の直角三角形の縦の辺の長さを表す。(先端の角度が “θ”)
- θは、半径 “1” の扇形の円弧の長さを表す。(先端の角度が “θ”)
- θがものすごく小さいときは、sinθ ≒ θ と近似できる。
- なんでそうなるのか、図に描くと一発で理解できる。
溢れでる涙を抑えられない!!
全11巻完結
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!
“sinθ” って何を表しているの?
まずは sinθ の意味から考えてみよう。
sinθっていうのは、下図のように直角三角形の斜辺と縦の辺の長さの比だ。これは問題ないでしょ。また、これを利用すると縦の長さは斜辺にsinθをかけたものになる。
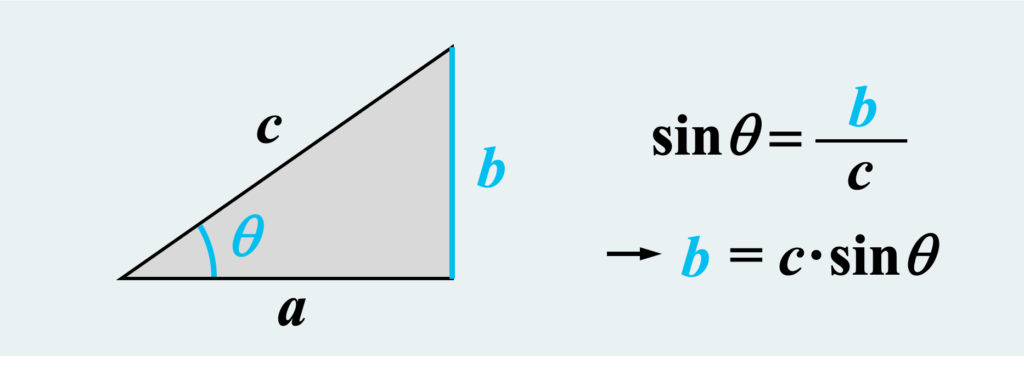
さらに、もう少し一般化して使いやすくするために、斜辺の長さが “1” のときはどうなるか?上の図で言うと、c = 1になる訳だから、縦の辺の長さそのものがsinθで表せることになる。
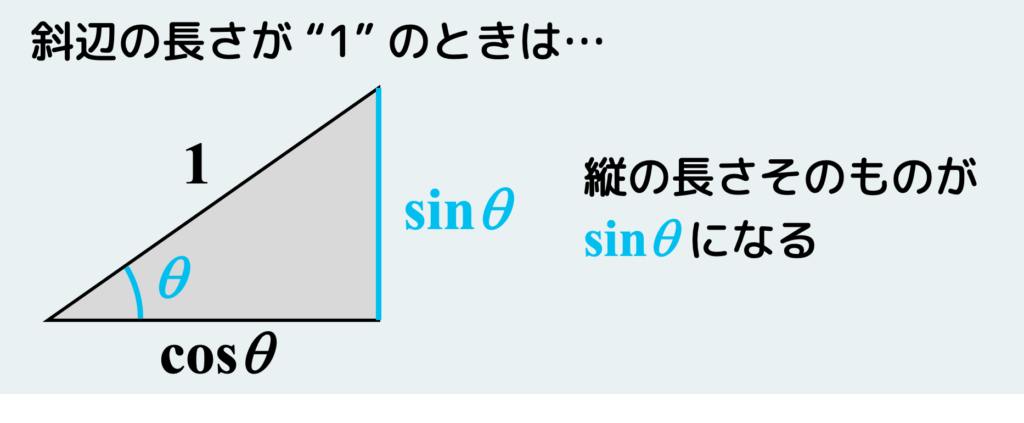
まずsinθの性質としてここまでをしっかりと理解しておこう。
じゃあ “θ” は何を表してるの?
では次に、θってなんだろうか?これは、前の記事でも書いたので、詳しく知りたい人はこれ(↓)を読んで欲しい。
 角度の単位(rad:ラジアン)とは?(°:度)やdegへの変換は?【番外1】
角度の単位(rad:ラジアン)とは?(°:度)やdegへの変換は?【番外1】
「sinθをθで近似する」ことができるのは、θが(°)ではなく(rad)で表されてるときだ。というわけで、前回の記事で説明したθ(rad)の重要な性質を思い出そう。
前回説明した通り、先端の角度が θ(rad)の扇形の円弧の長さは、(半径)×(角度)で表される。つまり、下図のような性質がある。
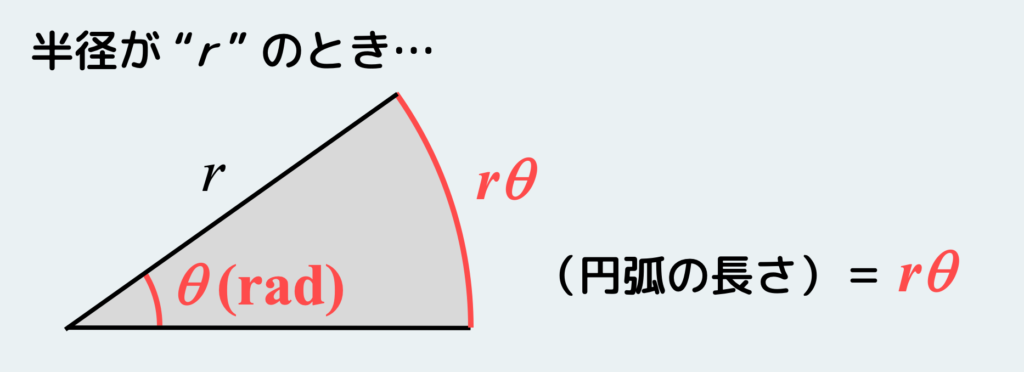
半径が “1” のときは、角度 θ(rad)の値がそのまま円弧の長さになるわけだ。
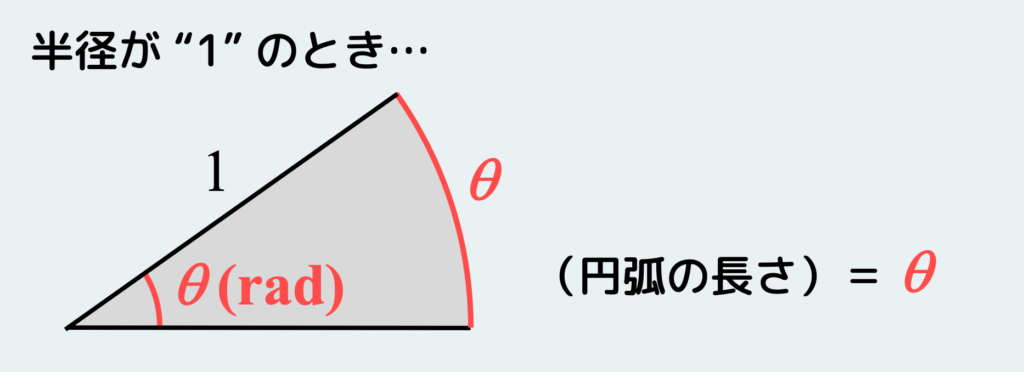
“θ” がものすごく小さいと・・
さあ「sinθ」と「θ」の基本的かつ重要な性質が分かったところで、この2つを結びつけていこう。
ところでこの近似「sinθ ≒ θ」には、重要な前提条件がある。それは、θがものすごく小さいということだ。θ が 1°とか 2° とか、そういうときは使えるって感じで、θが小さければ小さいほど近似の精度は高くなる(つまりsinθとθは同じ値に近付いていく)。
では、θがものすごく小さいとどんなことが起きるのか、図を交えて説明しよう。「sinθ」と「θ」を同時に考えたいので、斜辺と半径を共有したような直角三角形と扇形を描くと、「sinθ」と「θ」の関係は下図のようになる。
この図の先端の角度 θをどんどん小さくしていくと、直角三角形も扇形も細くなっていき、、、
結局下図のように、直角三角形の縦の辺(sinθ)と扇形の円弧(θ)がほぼ同じところを表すようになる。
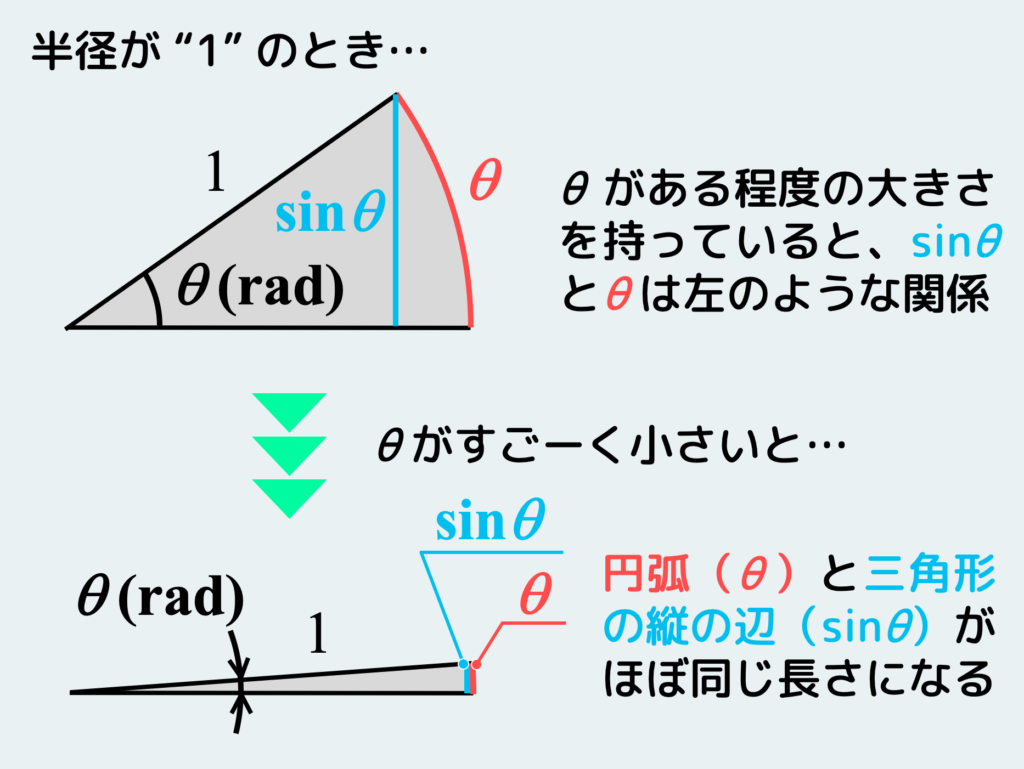
このように図を交えながら考えるとよく分かるだろう。
「sinθ ≒ θ」という近似は、θ(rad)が実は円弧の長さを表していることを利用したものだったわけだ。注意すべきことは、こういうところで出てくる角度θは(rad)で表されたもので、(°)ではないことだ。
- sinθは、斜辺の長さが “1” の直角三角形の縦の辺の長さを表す。(先端の角度が “θ”)
- θは、半径 “1” の扇形の円弧の長さを表す。(先端の角度が “θ”)
- θがものすごく小さいときは、sinθ ≒ θ と近似できる。
- なんでそうなるのか、図に描くと一発で理解できる。
研究者を志す者 必読!!
全8巻完結
こんなにも知的探究心を刺激される漫画があったとは!
真理のために命をかけた先人たちの物語。
この作品は、現役研究者である私・ぽるこが衝撃を受けた作品として、特に研究者およびこれを志す者には強く本気でオススメします。今ある常識を疑う心、誰に何を言われようと真理を追求する姿勢に触れ、心が動くこと間違いありません。
私自身、世界のトップ研究者だった師匠によく言われた言葉を思い出します。“目の前の現象に楽な答えを持ち出し、疑うことをやめ、真理の追求という困難な道から逃げていないか!?”
本作はこういった研究者の気概なるものを感じる、必読の価値ある一冊です。全8巻ですでに完結していますし比較的手軽に一気読みできます。気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!






