この記事では前回に引き続き、座標変換に関して解説していきたいが、前回の「応力」とは違い今回は「ひずみ」に関する座標変換だ。
「ひずみ」の座標変換についても、「応力」のときと同じくややこしい式が並び、しかも何のためにやってるのかよく分からない学生も多いだろう。
この記事では、ひずみの座標変換公式とその使い所、ついでにひずみを計測するためのセンサーである「ひずみゲージ」についても簡単に説明するので、ぜひ読んでみてほしい。
似たようなテーマで『応力の座標変換』がある。これについては下記の別記事で解説しているので、こちらを読んで欲しい。
 応力の2次元座標変換の公式の使い方・何のために使うのか徹底解説!【材力Vol. 5-1】
応力の2次元座標変換の公式の使い方・何のために使うのか徹底解説!【材力Vol. 5-1】
- 「ひずみ」も応力と同じく、材料中の同じ位置でも方向が変わればひずみ量は変わる。
- ひずみの座標変換公式を使えば、x-y座標系のひずみ状態をもとに、あるθだけ傾いた座標系のひずみ状態を計算できる。
- 異なる3つの方向の垂直ひずみを計測すれば、座標変換に基づき、その位置の二次元ひずみ場(εx・εy・γxy)がすべて算出できる。これすなわち、主ひずみの大きさや方向、さらには応力場や主応力などもすべて把握できることを意味する。(この手法をロゼット解析と呼ぶ)
夢へ駆ける少女の姿に感涙!!
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか?」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい!」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanならなんと3巻まで無料で読めてしまいます!まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです!
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!
Contents
ひずみの座標変換とは?
ひずみも応力と同じで、同じ位置でも見る方向によって、そのひずみの大きさは変わってくる。
大変イメージがわきにくいと思うので、下のような例を考えてみよう。
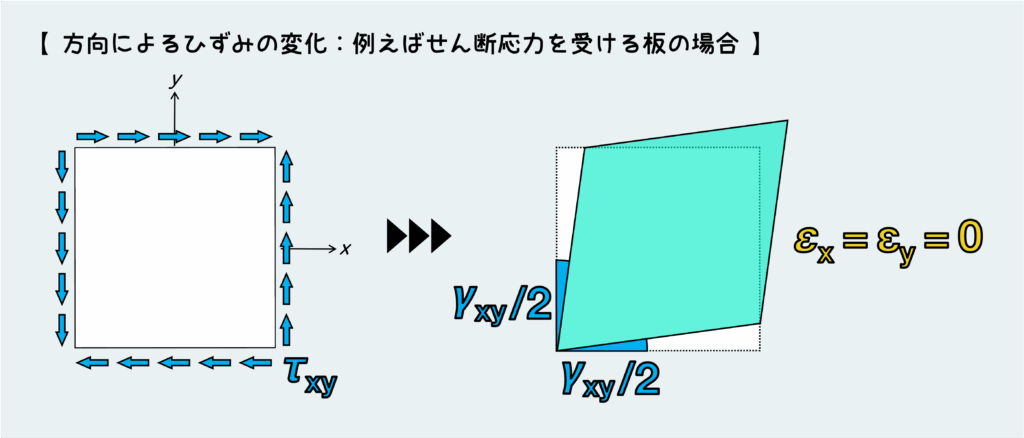
この例では、四角い板にx-y方向にせん断応力が作用している。変形をイメージしやすいように、ゴムみたいな割と変形しやすい材質を頭に思い浮かべてもらうといいかもしれない。
せん断応力が負荷される場合、当然x-y方向に発生するのはせん断ひずみであり、これは図の右側に描いているような形のゆがみ(角度のゆがみ)として現れる。
垂直ひずみのようにx-y方向には伸びたり縮んだりしている訳ではなく、真四角だったものが平行四辺形のようにゆがんでしまうってことだ。
もう少しわかりやすくイメージするために、下図のようにこの板がいくつかの帯状のものの集まりだとしよう。
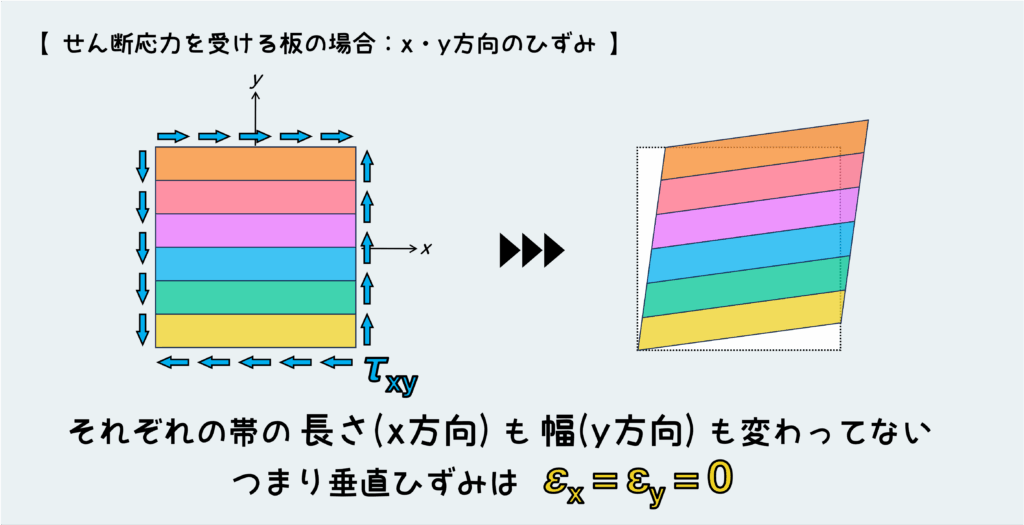
この場合、変形後の状態を考えると、それぞれの帯は長くなったりもしない(x方向の垂直ひずみ=”0″)し、幅も変わらない(y方向の垂直ひずみ=”0″)。
各帯の形状が長方形状から平行四辺形になっているだけである。
以上が、x-y方向にせん断応力が作用する状態において、『x-y方向の垂直ひずみ・せん断ひずみ』を考えた場合の話である。
では次に、同じ応力を受ける状態において、『違う方向のひずみを考える』とは一体どういうことなのか説明しよう。
下図のように、今度は45°傾いた方向に帯状のものが並んでるとして、このとき帯がどういう変形をしているかを考えてみよう。
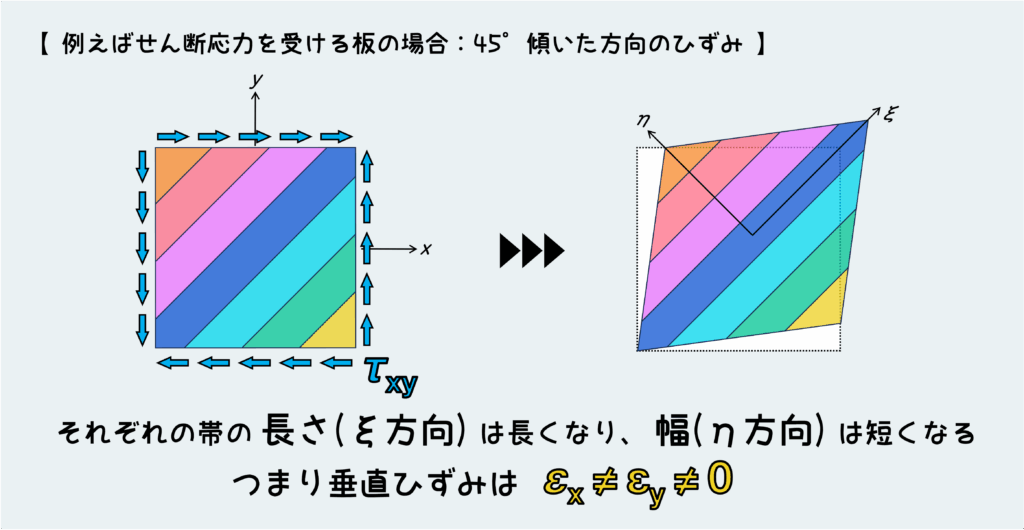
そうすると見ての通り、各帯の長さは長くなり(ξ方向の垂直ひずみ>”0″)、幅は短くなる(η方向の垂直ひずみ<“0″)となることが分かると思う。
つまりx-y方向においては垂直ひずみは存在しなかったが、見る方向を変えて45°傾いた方向(ξ-η方向)を考えると、何かしらの垂直ひずみが存在している訳である。
このように同じ応力を受ける材料の同じ位置だとしても、見る方向が変わればひずみ量は変わってしまうのである。
ひずみの座標変換は、このような方向によるひずみ量の変化を表すためのテクニックで、具体的にはある座標系のひずみ量(εx、εy、γxy)を元に別の方向のひずみ量(εξ、εη、γξη)を計算するための手法である。
ひずみの2次元座標変換の公式
ひずみの2次元座標変換公式は下図の通りだ。
x-y座標系のひずみ(εx、εy、γxy)が既知のものとして、これを元に反時計回りにθだけ回転したξ-η座標系のひずみ(εξ、εη、γξη)を計算するための公式だ。

応力のときと同じくやや複雑な形だが、無理やり覚える必要はない。必要なときに、教科書なりを見て正しく使えるようになっておくことが重要だ。
ひずみの座標変換の具体例(ロゼット解析)
ひずみの座標変換を使う具体例の一つとして、ひずみゲージを用いたロゼット解析を説明しよう。
ロゼット解析というのは、下図のように異なる方向に貼った3枚のひずみゲージの測定値を元に、その点の応力・ひずみに関する色々な量を算出するものだ。
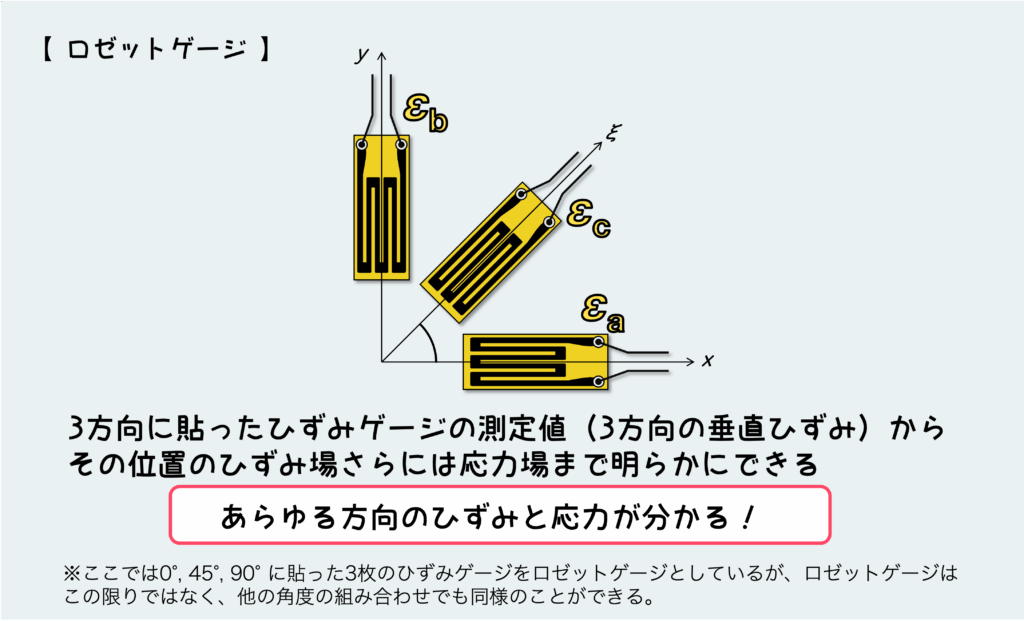
一軸に荷重がかかってるだけだとか、シンプルな構造の場合はこのような解析は不要だが、複雑な条件の場合は構造のどの方向に主応力が働き、どの方向が最も大きくひずむのか(主ひずみ)が明らかじゃないケースがある。
そんなときにこのロゼット解析を活用すれば、ある点にどのような応力・ひずみが発生しているのかを把握できるということだ。
以下では、この3枚のひずみゲージの出力値からどのようにして応力場やひずみ場を計算していくのかを簡単に説明したい。
※実際にはこの計算過程を自分で計算できる必要はなく、必要に応じてできあがった式を正しく使うことが重要だ。
まず1枚1枚のひずみゲージは何を測定しているかというと、貼られたその方向の垂直ひずみを測定している。
なので、x方向・y方向それぞれに貼られたひずみゲージの測定値εaおよびεbはそれぞれ、x方向・y方向の垂直ひずみεxおよびεyを表している。つまり、εx=εaであり、εy=εbである。
45°方向(ξ方向)に貼ったゲージはもちろん、このξ方向の垂直ひずみを表しているため、εξ=εcである。
さて、このεξ(=εc)は上記の座標変換公式の中にθ=45°を入れることでεx・εyおよびγxyで表現できる。
この式中のεx・εyはさっき言った通りεx=εa、εy=εbなので、この式をうまいこと変形すると、γxyを3枚のゲージ出力εa・εbおよびεcを使って求めることができる。

ひずみゲージの測定から直接的にせん断ひずみを測定することはできないが、このようにロゼット解析を行うことでx-y座標系のひずみ場(εx・εyおよびγxy)をロゼットゲージ測定から知ることができる訳だ。
ひずみ場が分かるってことは、その他諸々の情報が芋づる式に分かるということを意味している。
この同じ位置における主ひずみ(最大の垂直ひずみ)εmaxと最大せん断ひずみγmaxは(εx・εyおよびγxy)から公式的に求まる。(下図↓)
これに、さっき求めた(εx・εyおよびγxy)を(εa・εbおよびεc)で表現した式を代入することで、εmaxとγmaxも(εa・εbおよびεc)で算出することができる。(下図↓)

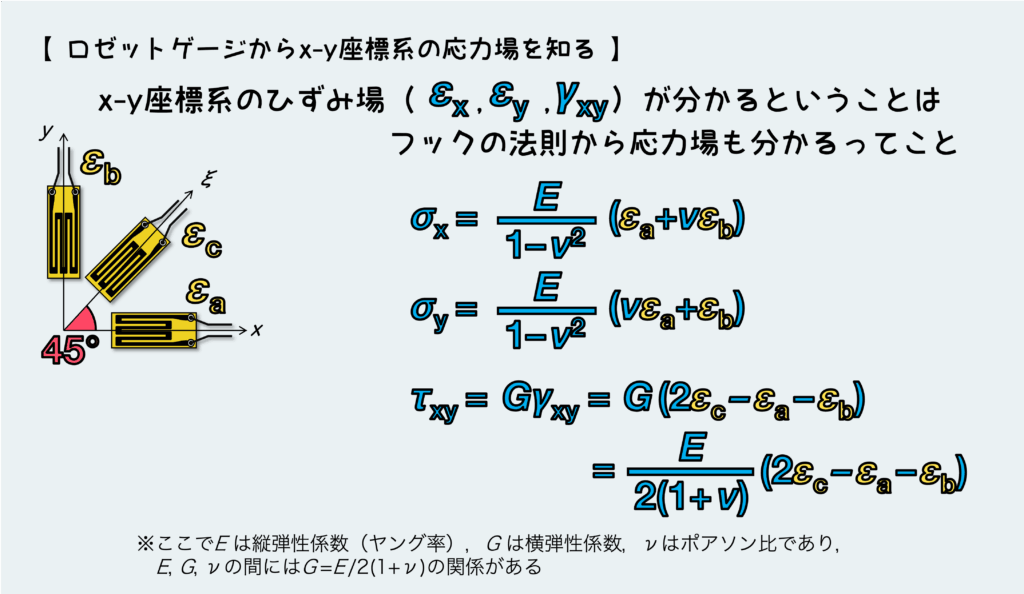
x-y座標系のひずみ場(εx・εy・γxy)が分かるってことは、フックの法則から応力場(σx・σy・τxy)も同様に分かるということだ。
ひずみと応力の間には、弾性範囲においてはフックの法則が成り立つ。このとき、変形のしにくさを決める材料定数である縦弾性係数E、横弾性係数G、ポアソン比νが必要になる。
この辺のフックの法則の話は別の記事にまた詳しく書くとして、2次元のフックの法則の公式(下図↓)を使うことでひずみ場から応力場を求めることができる。
これまた式変形して、応力場(σx・σy・τxy)を(εa・εbおよびεc)から求める式が得られる。
さて、最後に主応力(最大垂直応力)σmaxと最大せん断応力τmaxを求める式も考えてみよう。
主応力や最大せん断応力についての詳しい解説は別の記事に譲るとして、とにかくこれらは応力の座標変換の延長として、応力場(σx・σy・τxy)から計算することができる。
まあまあややこしい式変形をしていくと、下図のように主応力(最大垂直応力)σmaxと最大せん断応力τmaxをロゼットゲージの3つの測定値(εa・εbおよびεc)から算出する式を得ることができる。
 応力の2次元座標変換の公式の使い方・何のために使うのか徹底解説!【材力Vol. 5-1】
応力の2次元座標変換の公式の使い方・何のために使うのか徹底解説!【材力Vol. 5-1】

このように、ロゼットゲージで得られる3つのひずみ値(εa・εbおよびεc)から、ロゼットゲージを貼った位置のあらゆる情報を得ることができる。
この解析の基盤になっているのが、今回のテーマである「ひずみの座標変換」という訳だ。
まとめ
ひずみの座標変換テクニックについて解説したが、いかがだろうか?
応力の座標変換のときと同じく、座標変換の公式を覚える必要はないし、座標変換自体はそこまで重要じゃない。
重要なのは、ひずみも方向が変わればひずみ量は変わるということをよく理解することであり、必要に応じて座標変換公式を参照して正しく計算できるようになることだ。
- 「ひずみ」も応力と同じく、材料中の同じ位置でも方向が変わればひずみ量は変わる。
- ひずみの座標変換公式を使えば、x-y座標系のひずみ状態をもとに、あるθだけ傾いた座標系のひずみ状態を計算できる。
- 異なる3つの方向の垂直ひずみを計測すれば、座標変換に基づき、その位置の二次元ひずみ場(εx・εy・γxy)がすべて算出できる。これすなわち、主ひずみの大きさや方向、さらには応力場や主応力などもすべて把握できることを意味する。(この手法をロゼット解析と呼ぶ)
研究者を志す者 必読!!
全8巻完結
こんなにも知的探究心を刺激される漫画があったとは!
真理のために命をかけた先人たちの物語。
この作品は、現役研究者である私・ぽるこが衝撃を受けた作品として、特に研究者およびこれを志す者には強く本気でオススメします。今ある常識を疑う心、誰に何を言われようと真理を追求する姿勢に触れ、心が動くこと間違いありません。
私自身、世界のトップ研究者だった師匠によく言われた言葉を思い出します。“目の前の現象に楽な答えを持ち出し、疑うことをやめ、真理の追求という困難な道から逃げていないか!?”
本作はこういった研究者の気概なるものを感じる、必読の価値ある一冊です。全8巻ですでに完結していますし比較的手軽に一気読みできます。気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!





