さあこの材力解説シリーズもようやくVol. 5まで来た。Vol. 5では応力に関してさらに掘り下げていきたい。
この記事では、応力の座標変換について解説していく。材力の中でまあまあややこしい公式が登場するところなので、ぼく自身もあまり好きではないし、学生にとってもイメージしにくくて苦手な人が多いテーマなのではないだろうか。
応力の座標変換って何のためにやるのか？から公式とその使い方、具体例まで詳しく解説するので、この辺のテーマが苦手な人はぜひ読んでみてほしい。
- 材料中の同じ位置でも、見る面の方向が変わればその面に働く応力の状態も変わる。
- 応力の座標変換公式を使えば、x-y座標系の応力状態をもとに、あるθだけ傾いた座標系の応力状態を計算できる。
- 引張だけとか曲げだけ、のような単純な負荷形式の場合は応力の座標変換を考慮する必要は基本的にはないが、引張・曲げ・ねじりが複雑に組み合わさった状態の場合は応力の座標変換を元にどの面（どの方向）にどんな応力が働くのかを考えることが重要である。
- 溶接のように、ある特定の面（方向）の応力が重要になる場合は、仮に単純な引張の問題だとしても応力の座標変換を考える必要がある。
夢へ駆ける少女の姿に感涙！！
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか？」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい！」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanならなんと3巻まで無料で読めてしまいます！まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです！
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
Contents
応力の座標変換とは？
そもそも応力というのは『ある面に対して働いている負荷の大きさ』で定義されるものなので、材料中の位置だけでは決まらない。どの面（方向）に働いている応力か？ということも重要なことだ。
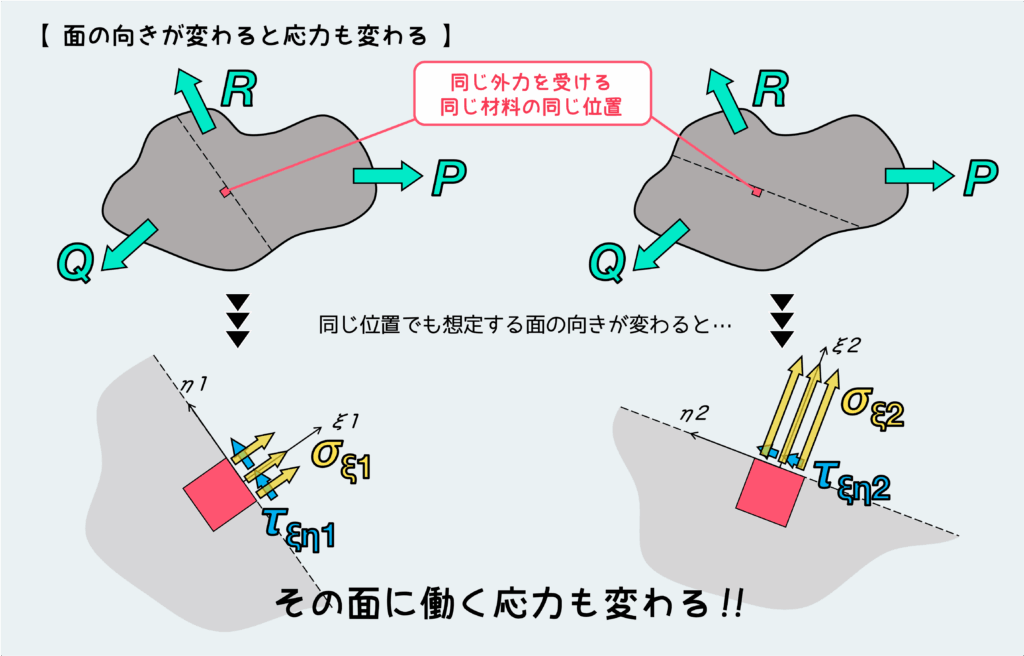
これまで扱ってきたような単純な引張・圧縮問題なんかでは、引張・圧縮を受ける棒の横断面に働く応力を対象にしてきた。σ=P/Aという公式で計算していた応力は横断面に作用する応力だ。
単純な引張・圧縮問題ではこの横断面に働く応力を相手にしていれば基本的に十分だった訳だが、実はこのような状況でも、これまで考えなかっただけで別の断面に働く応力を考えることももちろん可能である。
重要なことは、位置が同じだとしても見る面が変わると、その面に働く応力の大きさや種類が変わってしまうことだ。
単純な引張を受ける棒の横断面にはσ=P/Aの引張応力が作用している訳だが、同じ位置で見る面の方向を変えるとその面にはσ=P/Aとは違う大きさの垂直応力が作用している。先ほどの横断面には発生していなかったせん断応力まで発生する。
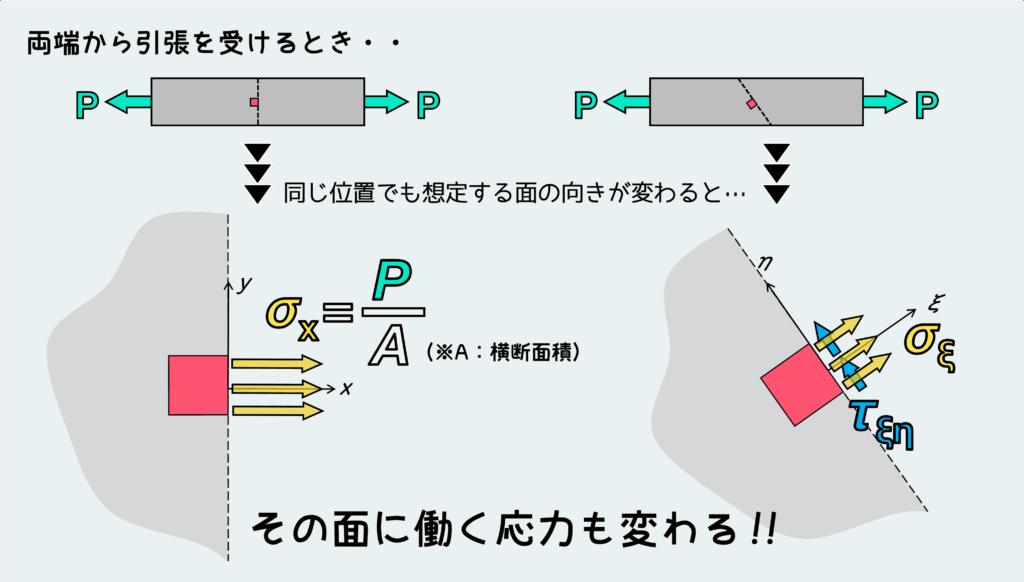
応力の座標変換というのは、ある向き（x-y座標系）の面に働く応力状態を元にして、それとは違う向きの面に働く応力状態を導き出すためのテクニックである。
ではどんなときに座標変換をやる必要があるのか？
色んな状況があると思うが、例えば繊維状の材料だとか、もっとイメージしやすい例で言うと「さけるチーズ」的なもので座標変換が必要になるケースがある。このような材料は方向によって強さが違う材料で（異方性材料と言う）、ある方向には強いけどある方向には弱いみたいな特性を持つ。
こういう場合には、そういう特定の弱い面に働く応力を把握することが重要になる。つまり、方向によって材料の許容応力値が異なるので、例えば横断面に働く応力がその面の限界値を超えないとしても、別の方向の面（弱い面）に働く応力がその弱い面の限界値を超えると壊れてしまう。
このような時、座標変換を使ってそのような特定の面に働く応力を知ることが必要になる。
応力の座標変換の公式
2次元問題における応力の座標変換は下図の通りだ。
これは、x-y座標系の応力状態（σx、σy、τxy）を元に、θだけ傾いたξ-η座標系の応力状態（σξ、ση、τξη）を算出するための公式だ。
若干複雑なので覚える必要はないと思う。（教える先生によっては「覚えろ」と言われるかもしれない）
重要なのは適切に使えるようになっておくことだ。ということで、これ以降では具体的な事例を交えて、座標変換公式の使い方を紹介しよう。
応力の座標変換が必要になる具体例
これが最も簡単イメージでき、かつ実際に起こり得るケースだと思われる。
詳細は下の図を参照してほしいが、2つの棒を斜めの面で接着して1本にした部材があるとしよう。これを両端から引っ張ることを考える。
この『棒を両端から引っ張る』というシチュエーション自体は極めてシンプルなものなので、とても見慣れたものだろう。この材料の横断面に働く応力は当然、σ=P/Aで算出することができる。
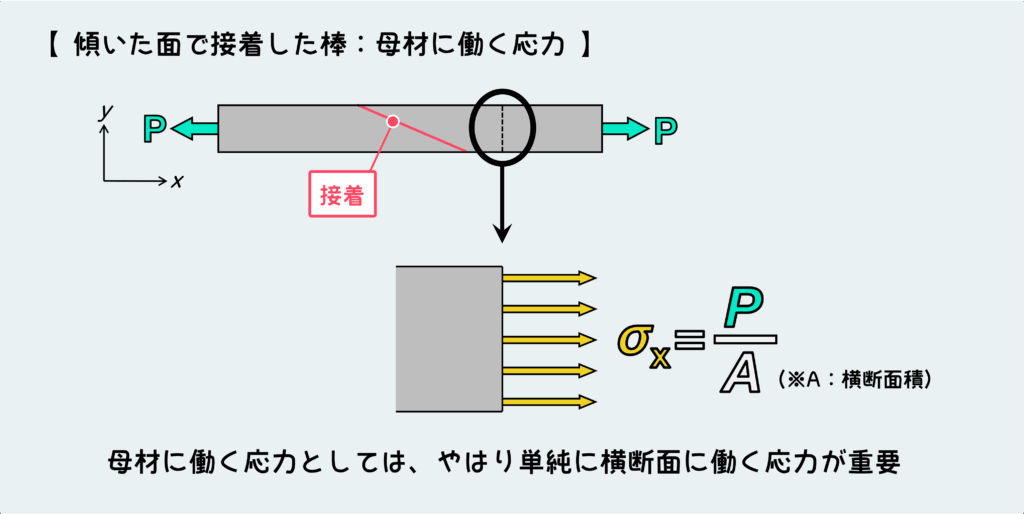
もちろんこれ自体は何も間違っていない。なので、この接着している材料自体（溶接や接着している状況では“母材”と呼んだりする）に働く応力やそれによる母材の破壊を考慮する場合は、このσ=P/Aで求まる応力を相手にしていればよい。
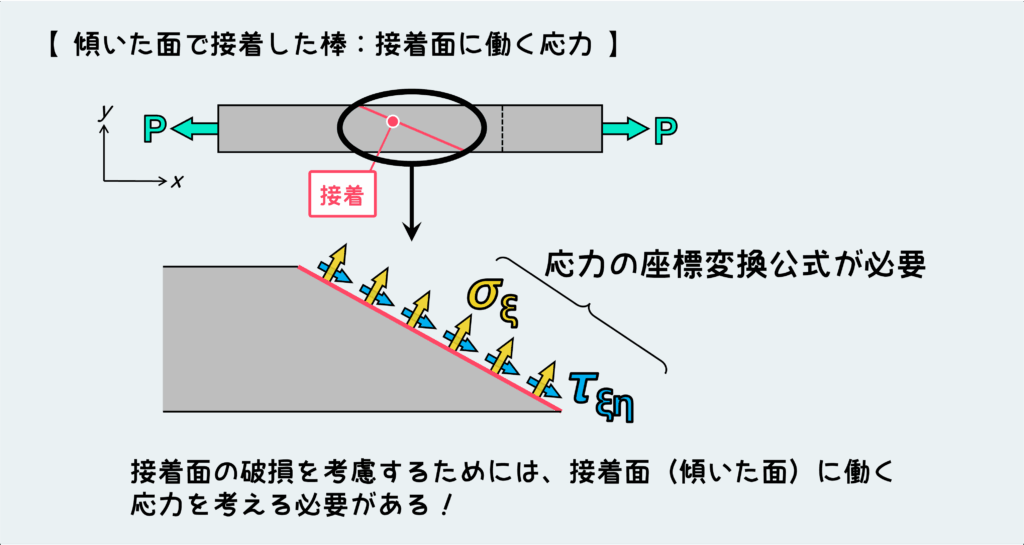
しかし、こういう接着や溶接のシチュエーションでは、一般的に母材の強度よりも接着部の強度の方が低いことがよくある。母材が大丈夫だとしても、接着部に働く応力により接着部が破壊する場合があり、これを懸念しないといけない。
つまり、ここで重要なのはこの接着面に働く応力（垂直応力およびせん断応力）である。これが接着剤のもつ引張強度やせん断強度を超えてしまえば、この接着部ははがれてしまうということだ。
この接着面（傾いた面）に働く応力を算出するために、上で示した座標変換の公式を使うことになる訳だ。
では、実際に数値を使って計算してみよう。
ここでは接着剤として名高い『アロンアルファ』を例にとって計算してみよう。色々なサイトを見たところ、アロンアルファの引張接着強度は40MPa程度で、接着せん断強度は20MPa程度らしい。（この数値自体の信憑性は保証できないので、あくまで計算のための例として考えてください）
下図のように、直径10mmの丸棒を長手方向（図のx方向）から30度傾いた面で接着して、15kNで引っ張ることを考えてみよう。ちなみにこの部材は鉄鋼製で降伏応力は250MPaとする。
この部材の横断面には、σx=P/Aで求まる垂直応力が作用し、これは部材の降伏応力よりも十分小さいので、この部材自体の破損や変形は特に気にする必要はない。ちなみに一軸引張なので、σy、τxyともに“0”である。
一方、接着面に働く応力はどうだろうか？
30度傾いた面に働く応力を、σx=P/A、σy=τxy=0を元に座標変換公式を使って計算すると下図のようになる。見ての通り、この接着面に働く応力はアロナルファの接着強度を超えてしまっている。すなわち、この仕様では接着部がはがれて構造の破損を招く可能性が極めて高いということになる！
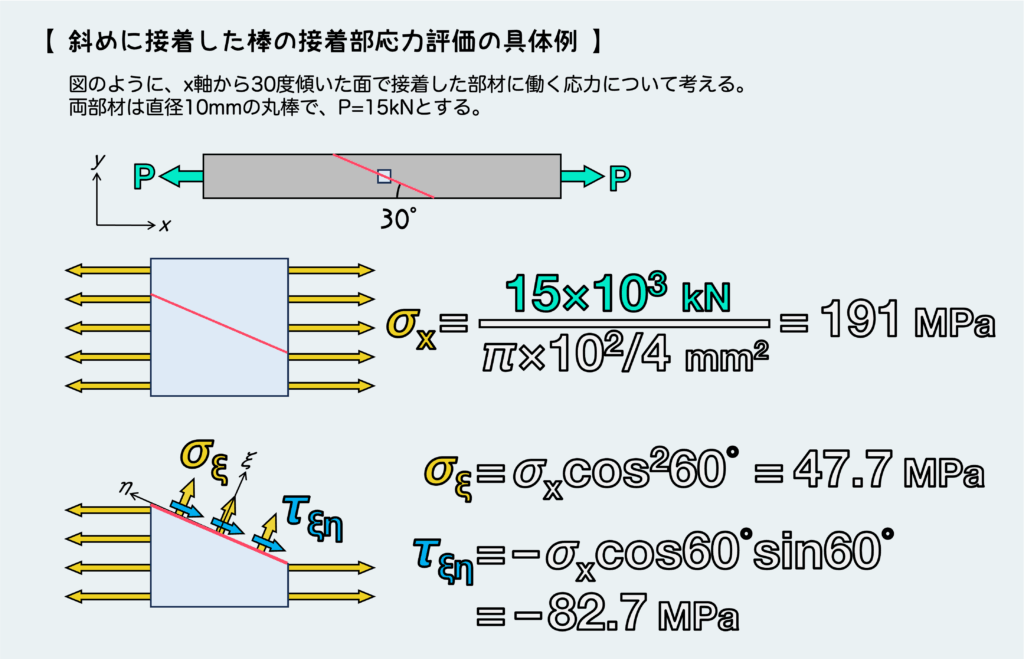
ちなみに、座標変換の式中のθに何をいれるべきかは間違えないようによく注意してほしい。この例題では『30度傾いた』という記述をしているが、式にいれるべき角度は『60度』である。
まとめ
いかがだろうか。
上の例で座標変換公式の使い所とその重要性が分かってもらえただろうか。
公式はやや複雑なので個人的にはわざわざ暗記する必要はないと思うが、いざ必要なときには教科書を開いて、傾いた面の応力をしっかり計算できるようになっておいてほしい。
この章のこれ以降の記事では「ひずみの座標変換」と「主応力」について掘り下げていきたい。特に「主応力」は、部材の安全性を検証する上で超大事なのでぜひご一読いただきたい。
- 材料中の同じ位置でも、見る面の方向が変わればその面に働く応力の状態も変わる。
- 応力の座標変換公式を使えば、x-y座標系の応力状態をもとに、あるθだけ傾いた座標系の応力状態を計算できる。
- 引張だけとか曲げだけ、のような単純な負荷形式の場合は応力の座標変換を考慮する必要は基本的にはないが、引張・曲げ・ねじりが複雑に組み合わさった状態の場合は応力の座標変換を元にどの面（どの方向）にどんな応力が働くのかを考えることが重要である。
- 溶接のように、ある特定の面（方向）の応力が重要になる場合は、仮に単純な引張の問題だとしても応力の座標変換を考える必要がある。
研究者を志す者 必読！！
全8巻完結
こんなにも知的探究心を刺激される漫画があったとは！
真理のために命をかけた先人たちの物語。
この作品は、現役研究者である私・ぽるこが衝撃を受けた作品として、特に研究者およびこれを志す者には強く本気でオススメします。今ある常識を疑う心、誰に何を言われようと真理を追求する姿勢に触れ、心が動くこと間違いありません。
私自身、世界のトップ研究者だった師匠によく言われた言葉を思い出します。“目の前の現象に楽な答えを持ち出し、疑うことをやめ、真理の追求という困難な道から逃げていないか！？”
本作はこういった研究者の気概なるものを感じる、必読の価値ある一冊です。全8巻ですでに完結していますし比較的手軽に一気読みできます。気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
