前の記事でねじり変形そして静定問題について解説をしてきたが、この記事では不静定問題の解き方について解説していきたい。
材料力学 ねじりによる変形（ねじれ角）と超基礎的な例題の解き方【材力Vol. 4-3】
不静定問題の唯一にして最大のポイントは『変形の条件』を見極めることだ。このことは、ねじりだろうが引張圧縮だろうが変わらない。解き方の流れは一緒だ。
この記事では、２つの例題を通してねじりの不静定問題および『変形の条件』の見極め方について理解を深めてほしい。
不静定問題の基本的な解き方の流れは、下記の記事でもふわしく解説しているので必要なら合わせて読んでいただきたい。
材料力学 引張・圧縮を受ける材料の不静定問題【Vol. 3-3】
- 不静定問題の基本は『変形の条件を見極め、それを正しく条件式化すること』であり、これは引張圧縮問題でも今回のねじり問題でもまったく変わらない。
- 複雑な問題もシンプルなパーツの組合せに分解し、それぞれの自由体に働く内力を想定し、個々の変形量から全体像を描く、という材力の王道を実践するのがもっとも大事。いっつも大事。
夢へ駆ける少女の姿に感涙！！
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか？」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい！」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanなら2/4までなんと3巻無料で読めてしまいます！まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです！
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
Contents
ねじれ角の公式をおさらい
まずは、ねじりの変形量（ねじれ角）の公式についておさらいしておこう。
両端にトルクTが働くシンプルな棒のねじれ角は下図のように表せる。
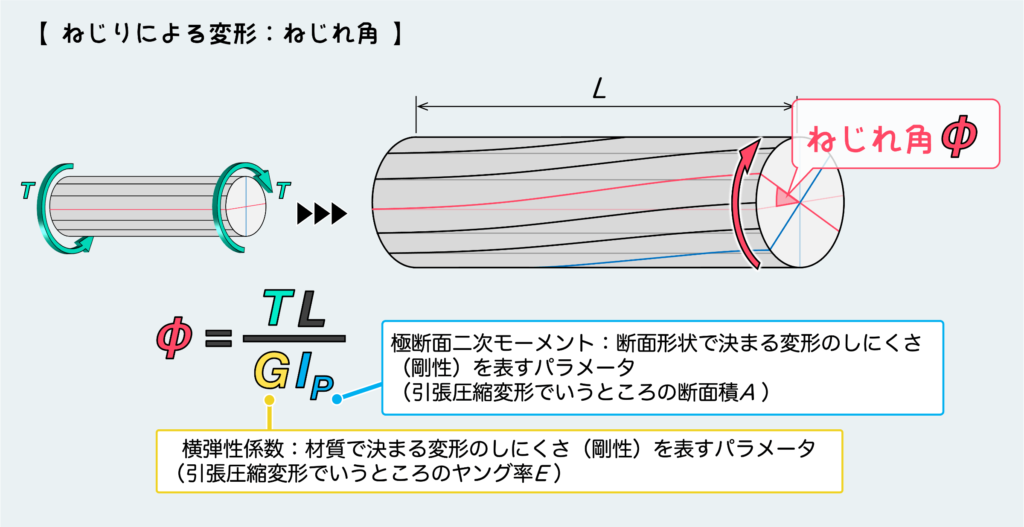
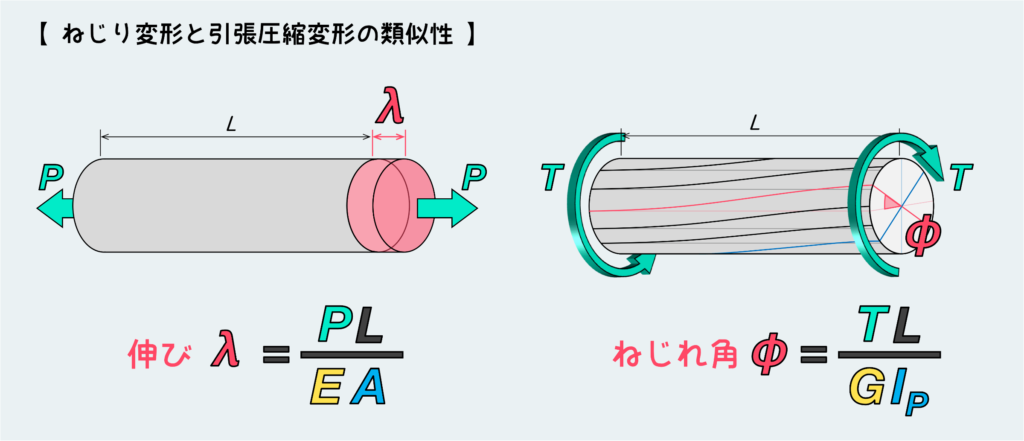
ねじれ角の公式は、横弾性係数Gや極断面二次モーメントIPが出てくるため少し慣れないこともあるかもしれないが、よくよく見ると引張圧縮による変形量・伸び縮みの公式と同じ作りになっていることに気が付くだろう。
下の絵で比較をしている通り、分子は作用している負荷の大きさ（P、T）と部材の長さ（Lで共通）の積であり、分母は剛性（ヤング率E、横弾性係数G）と断面形状パラメータ（断面積A、極断面二次モーメントIP）の積である。
それぞれ同じ性質のもので公式が形成されており、引張圧縮の変形量の公式さえ覚えておけば、新たにねじれ角の公式を覚える必要はないってことだ。
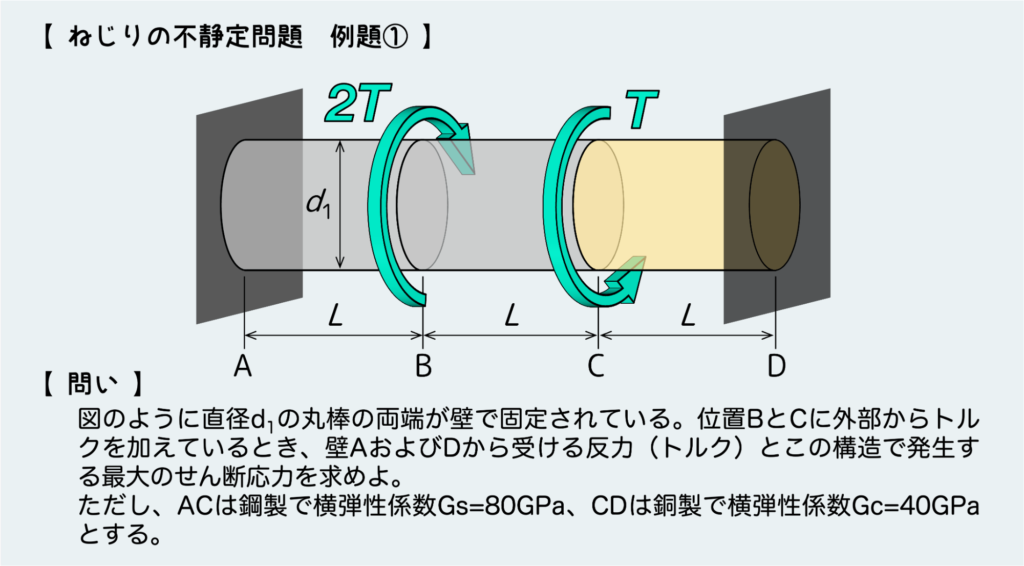
ねじりの不静定問題 例題①
１つ目の例題として下のような問題を考えよう。
両端を壁で固定した丸棒に対して外部から負荷を加える超定番の不静定問題だ。
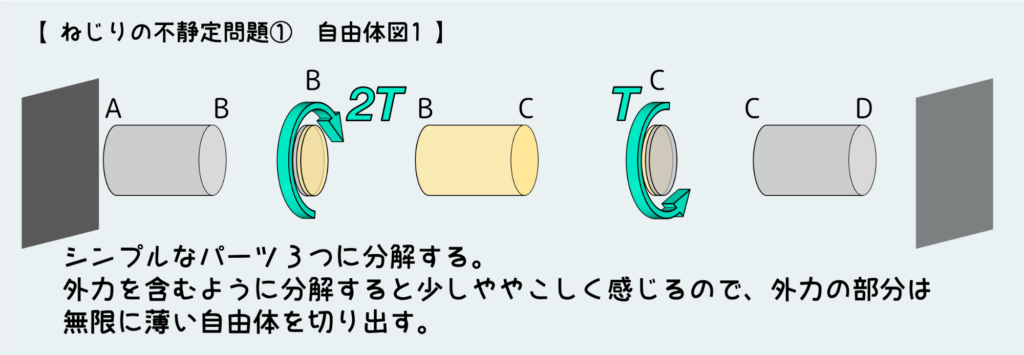
毎回言っていることだが、どんな問題もまずは構造体の内部にどんな風に内力が伝わってるかを把握する事から始まる。すなわちシンプルなパーツに分解して自由体図を完成させることがいつもスタート地点だ。
少し丁寧に自由体図を完成させるまでの経過を見ていこう。
まずは、外力が加わるポイントや形状や材質など何かしらが変化するポイントで分解する。これによってシンプルなパーツの組合せに分解する。
ここでのコツは『外力が加わっている点を無限に薄い自由体として別ものとして分解する』ことだ。
外力を含んだ状態で分解しようとすると、外力を分解した２面のどちらに描けばいいのか悩んでしまうかもしれない。実際どっちでも構わないのだが、悩んでしまうぐらいならもはや外力は外力だけで別の自由体として取り出してしまえばいい。
外力が加わっている箇所のみを無限に薄い自由体として取り出せば、外力の取り扱いに迷わなくてすむ！
分解したら、とっかかりになる場所（平衡条件を考えることができる自由体）がないので、まずは一番左の面に反力TAを仮置きしよう。
そしたら左から右側に向かって順番に、作用・反作用の法則と平衡条件を利用して内力の伝えていく。
下の絵に描いている通り、①→④の順番に力を伝えていけばいい。
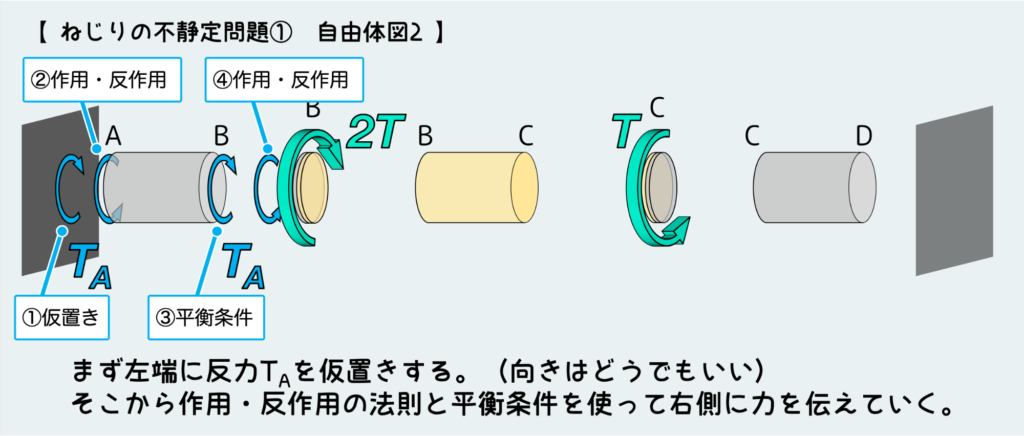
次に、外力が加わっているB面のつり合いを考えることになる。（下図の⑤）
ここで少し迷う人もいるかもしれない。2TとTAの大小関係がはっきりしないので、B面の右側の面にどっち向きに内力を想定すればいいのか分からないからだ。
結論として、この時点ではTAの中身が分からない以上どうしようもないので、適当な向きに仮置きしていい。ただし、平衡条件はちゃんと成り立つ必要がある。それだけは壊してはならない。
どっち向きに仮置きしてもいいが、平衡条件が成り立つように矢印の大きさを決定しなければならない。
内力の働く向きが決定できないところはどちら向きでもいいから仮置きしておけばいい。その上で平衡条件は必ず満足させる必要がある。
ここ（⑤）を通り過ぎれば、あとはまた右側に向かって作用・反作用の法則と平衡条件を駆使して内力を決定していく。
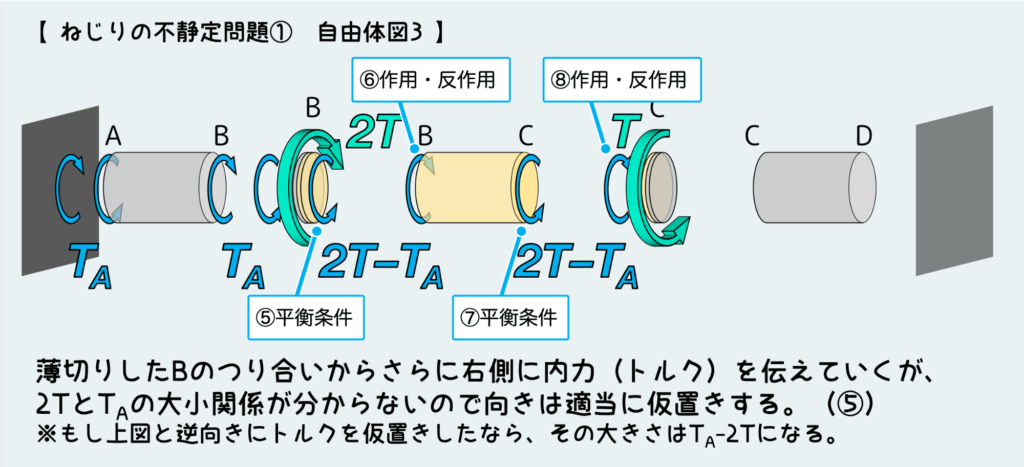
さっきと同じように外力が加わっているC面のつり合いについても、矢印の向きは適当に仮置きした状態で平衡条件を考える。（下図の⑨）
これで、反力TAが未知のままではあるものの自由体図全体が完成したことになる。
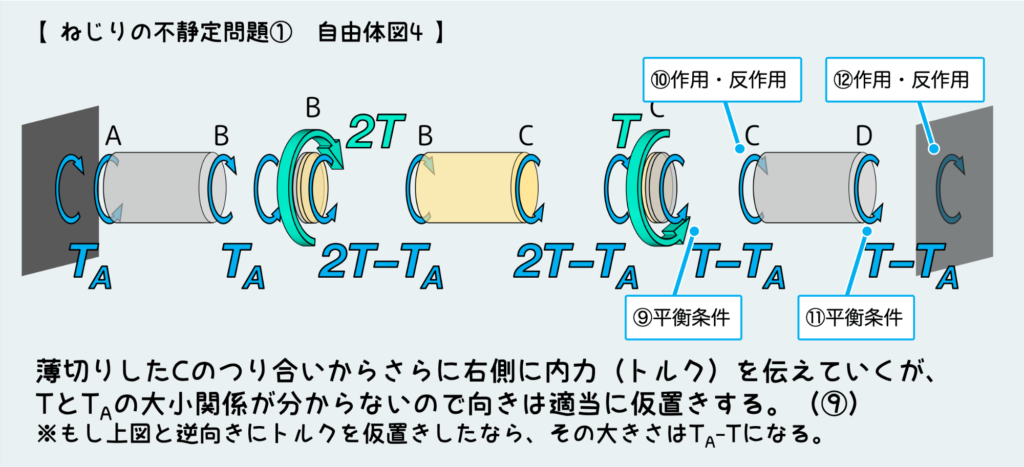
静定問題であれば、平衡条件と作用・反作用の法則だけで内力の全体像がすべて決まってしまうが、不静定問題では未知の内力が残ってしまう。今回のやり方だとそれが反力のTAという訳だ。
『変形の条件』を考えるために、まずは未知の内力を残したまま、分解した各パーツの変形量（ねじれ角）を計算する。どちら向きへの変形を間違えないように注意しよう。
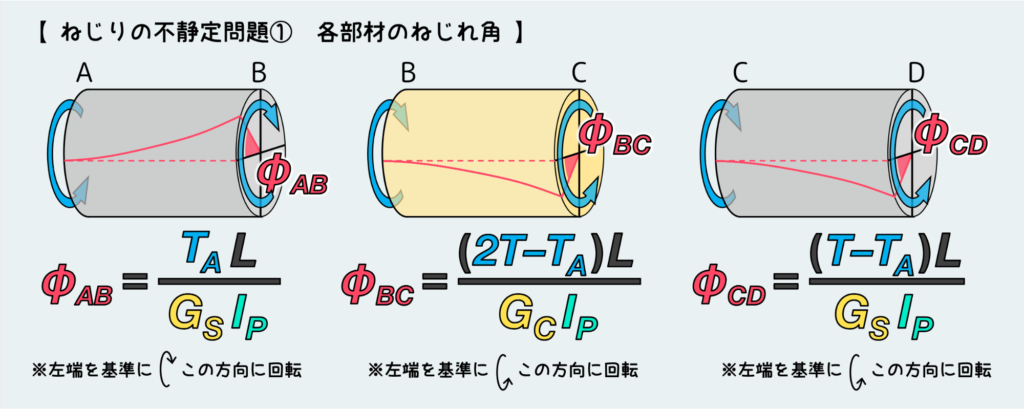
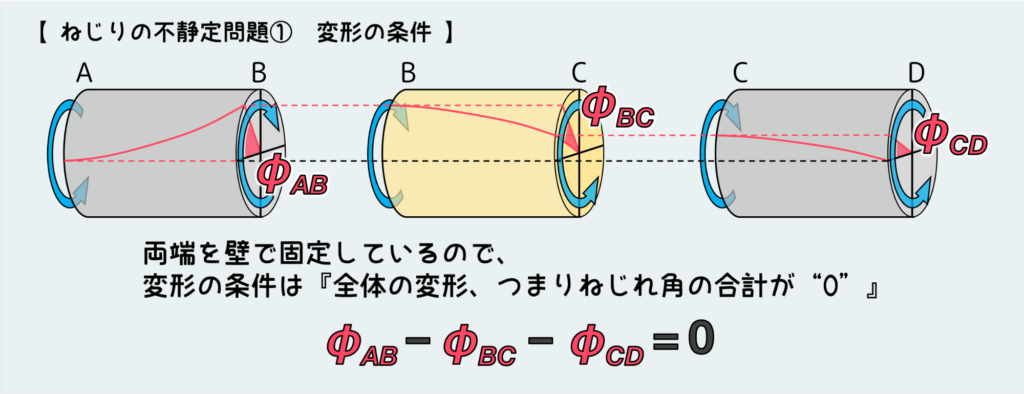
ここまで整理できたら、『変形の条件』を考えていこう。
今回は両端固定の問題で、めちゃくちゃ典型的な不静定問題だ。こういった問題の場合は両端の壁に接続している面が動けない（変位を持てない）ことが特徴なので、変形の条件としては「全体を通した変形の合計が”0″であること」になる。
つまり、ねじれの向きに注意して、下図のような変形の状態になる必要があるので変形の条件式としては「φAB-φBC-φCD=0」になる。
もし自由体図を完成させる上で、トルクをここで説明している解き方とは逆向きに仮置きした場合には、変形の向きが逆になるので、下の絵と条件式の中の正負が変わってくることになる。
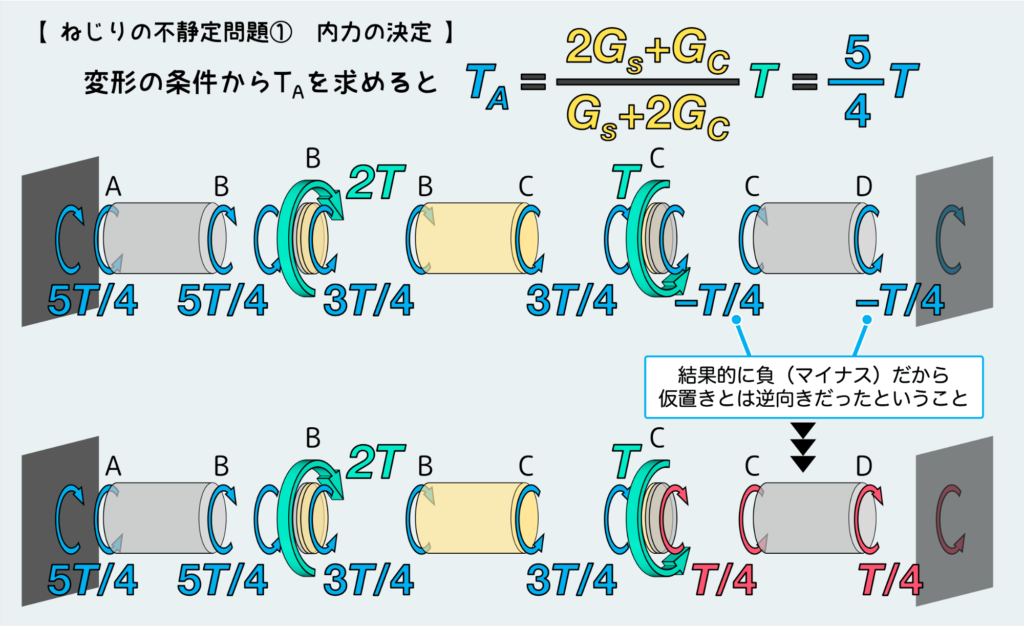
条件式を立てることができたら、これに各パーツの変形量（未知数TAを含む）を代入して、TAを決定する。
求めたTAを自由体図の中に組み込んでいけば、正しい全体像が浮かび上がってくる。
ここで、もし負（マイナス）になる量が出てきた場合は、仮置きしたトルクが結果的に逆向きだったことを示す。
これを考慮して、本当の内力の伝わり方を整理すると、下図の下半分のようになる。
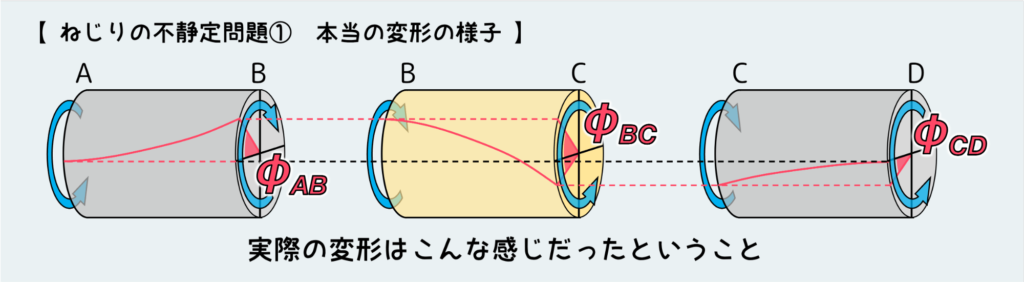
そうなると、変形の条件を式化する際に考えた変形の様子も少し変わってくる。
本当は下の絵のようになり、上で考えていた様子とはCD部分の変形方向が逆になっている。
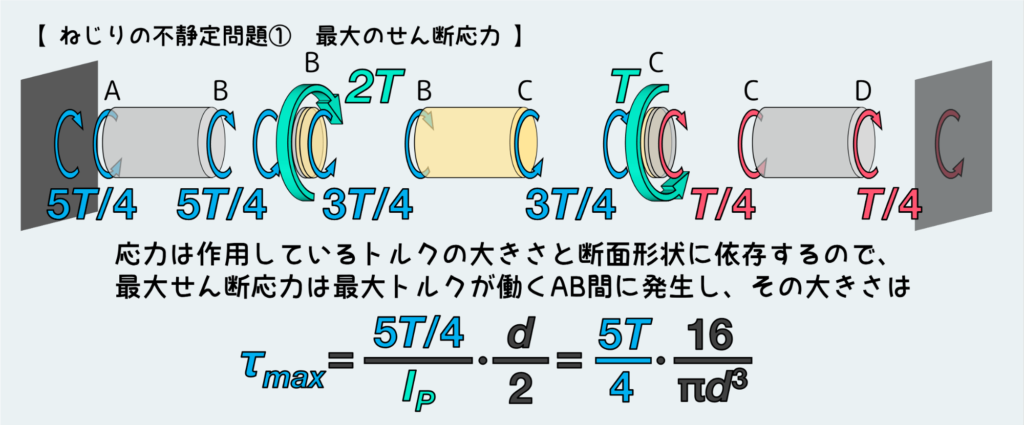
最後に、この構造体で発生する最大のせん断応力を考えよう。
トルクによるせん断応力は極断面二次モーメントIPと作用しているトルクの大きさに依存するので、今回の問題のように断面形状が一様な場合は最大トルクが働くところでせん断応力も最大になる。
つまり今回の問題ではAB間の部材表面で最大せん断応力が発生する。
計算については下の記事でせん断応力の公式の使い方を確認してもらいたいが、AB間に作用しているトルク5T/4を極断面二次モーメントで割って、中立軸から表面までの距離（d/2）をかけることで計算できる。
材料力学 ねじり（トルク）によるせん断応力の考え方【材力Vol. 4-2】
ねじりの不静定問題 例題②
さて、２つ目の例題として次のような問題を見てみよう。
外部からトルクを受ける丸棒の中央に剛体板が接続されており、その両端にワイヤーがつながっている。
この問題では丸棒のねじりによる変形とワイヤーの変形に折り合いをつけるような『変形の条件』を見出すことが肝となる。
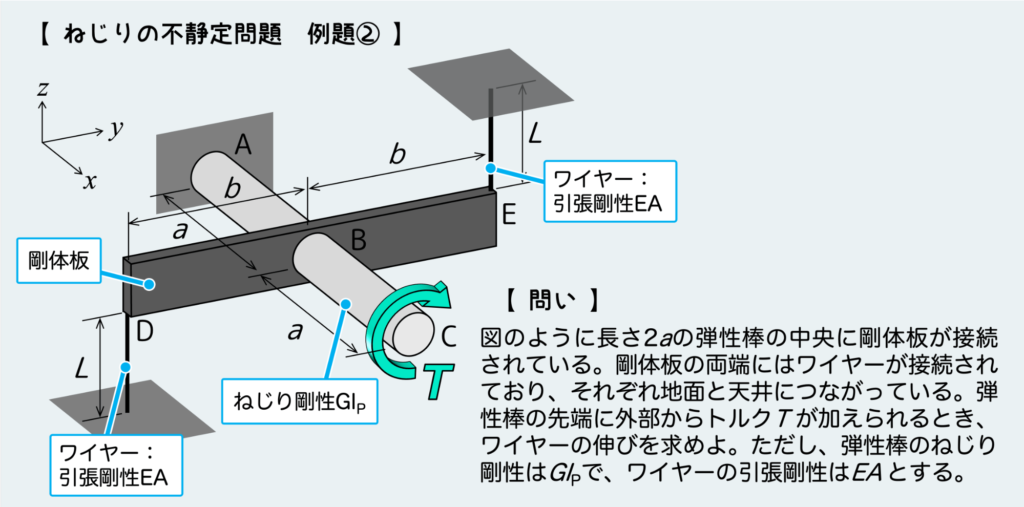
まずはいつもの通り、いくつかのパーツに分解していく。
慣れてくればできるようになると思うが、この問題を見た時点で、今回の変形の条件でキーとなるのは中央の剛体板の動きであろうことは予想できる。
なので、剛体板がどれだけ回転するのかを考える必要があり、そのためには丸棒ABがどれだけねじれるかを考えなくてはならない。そのため、Bのところで切断し、ABに働くトルクを想定してBのねじれ角を計算していく。
剛体板の両面で丸棒を切断し、さらにワイヤーも切断して、毎度同じく平衡条件と作用・反作用の法則を使って自由体図を完成させると下図のようになる。
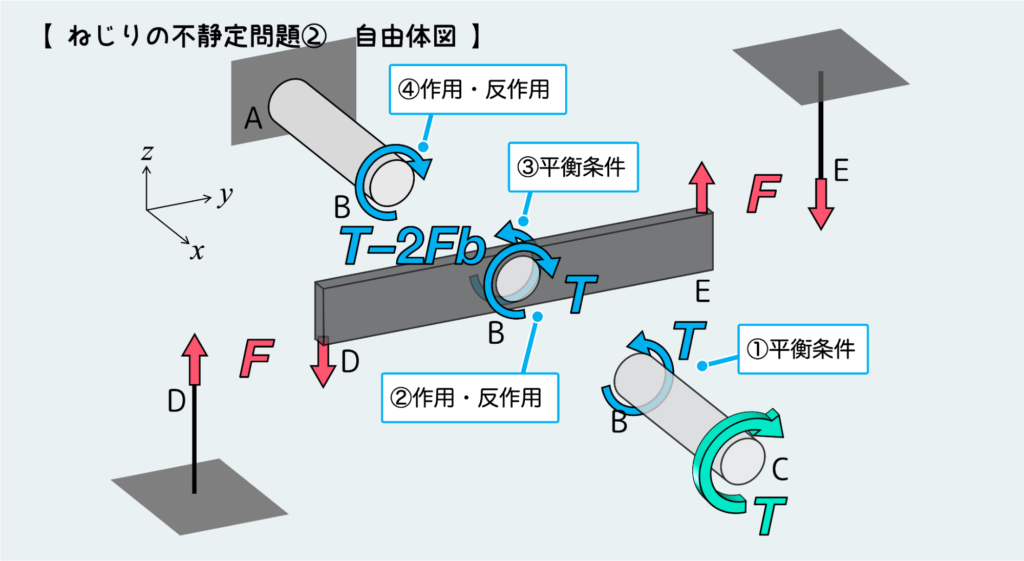
さて、変形の条件はどのように考えるか？
さっきも言ったが中央の剛体板が鍵である。剛体というのは力が加わっても全く変形しないものとみなせるので、この構造全体が変形しても剛体板DEの直線性はくずれない。
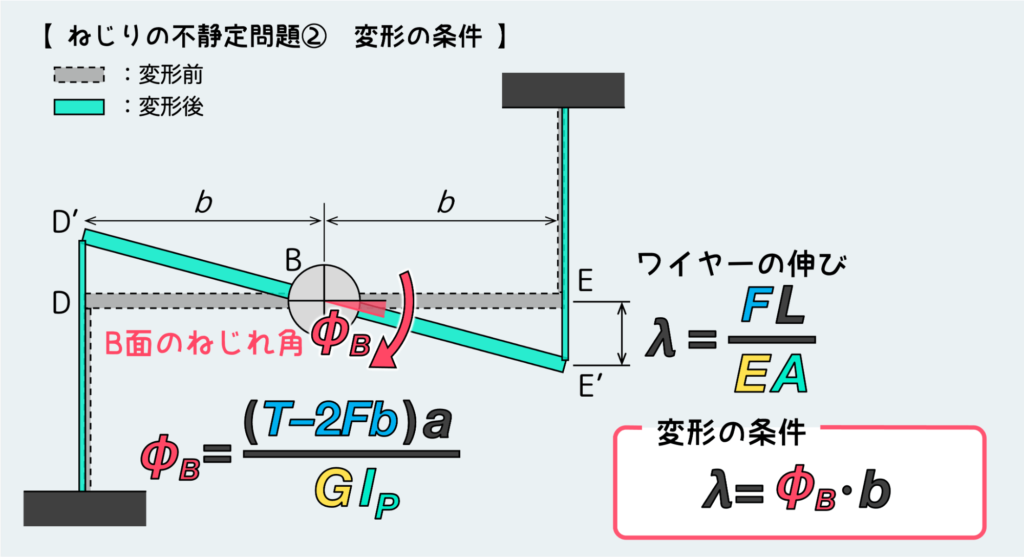
こういう時ほど図を描くことが重要である。下の絵では変形が分かりやすいように一部大袈裟に描いている。
下の絵の通り、B面が回転（ねじれ角φB）した分だけ剛体板DEが回転する。これに連れて両端に接続したワイヤーが伸びる。
すなわち、『回転によるD点およびE点の移動量とワイヤーの伸びが等しい』というのが今回の変形の条件だ。これを数式化すると『λ＝φB·b』となる。
ここで、なぜねじれ角φBによってD点およびE点の移動距離がφB·bになるか分からない人は下の記事を読んでほしい。（なぜか自分でも分からないが弊ブログで一番読まれている記事である）
「sinθをθで近似する」ってどうしてそうなるのか詳しく説明します。【番外２】
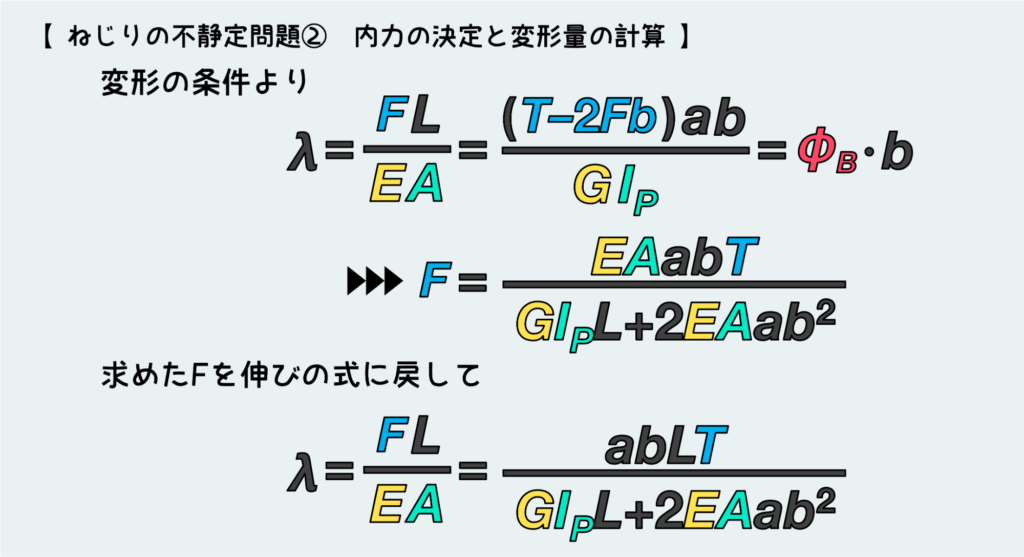
ここまで問題が整理できたら、あとは出来上がった式に変形量を代入してこねくり回すだけだ。
変形の条件式を作り替えていくと、ワイヤーに伝わる力Fが求まる。これをワイヤーの伸びの式に戻せば、ワイヤーの伸びλが無事求まるという寸法だ。
まとめ
不静定問題の解き方として『変形の条件』を見極めることが最も重要だということは、以前の記事ですでに詳しく説明しているので、この記事ではねじりの不静定問題の例題を２つ説明してきた。
この手の問題を解くには、変形の条件を正しく見出せるか？そしてそれを正しく数式化できるか？ということにかかっているのだが、結局はいろんな種類の問題を解いて慣れていくのが重要である。
この記事では比較的定番と言える２パターンを紹介したが、また別の記事で練習問題を紹介したいとは思っているので、気がむいた人はそちらもぜひご覧いただきたい。（記事執筆中）
- 不静定問題の基本は『変形の条件を見極め、それを正しく条件式化すること』であり、これは引張圧縮問題でも今回のねじり問題でもまったく変わらない。
- 複雑な問題もシンプルなパーツの組合せに分解し、それぞれの自由体に働く内力を想定し、個々の変形量から全体像を描く、という材力の王道を実践するのがもっとも大事。いっつも大事。
研究者を志す者 必読！！
全8巻完結
こんなにも知的探究心を刺激される漫画があったとは！
真理のために命をかけた先人たちの物語。
この作品は、現役研究者である私・ぽるこが衝撃を受けた作品として、特に研究者およびこれを志す者には強く本気でオススメします。今ある常識を疑う心、誰に何を言われようと真理を追求する姿勢に触れ、心が動くこと間違いありません。
私自身、世界のトップ研究者だった師匠によく言われた言葉を思い出します。“目の前の現象に楽な答えを持ち出し、疑うことをやめ、真理の追求という困難な道から逃げていないか！？”
本作はこういった研究者の気概なるものを感じる、必読の価値ある一冊です。全8巻ですでに完結していますし比較的手軽に一気読みできます。気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！