さて今回の記事では、トラス構造に伝わる力を切断法で考える方法について説明していきたい。
苦手な学生のみなさんも多いと思うので、ことさら丁寧に説明していく。ぜひ役に立ててほしい。
前回は節点法による考え方について解説したので、節点法について知りたい人はそちらの記事を読んでほしい。
材料力学 10分で絶対分かるようになるトラス問題（節点法による力の伝わり方編）【Vol. 3-4】
また変形の考え方については次の記事を見てほしい。
材料力学 10分で絶対分かるようになるトラス問題（変形量編）【Vol. 3-6】
では切断法について説明していこう。前半は節点法の記事と同じなので、そっちをすでに読んだ人は「切断法のやり方と簡単な具体例」まで飛ばしてもらって構わない。
- トラス部材には軸力しか働かない。これのおかげで強い構造体にできる。
- 各部材に働く内力を明らかにするには節点法と切断法がある。
- 節点法はすべての部材に働く力を明らかにしていき、ある点の変位を知りたい場合に使える。あまりにも複雑なトラスの場合は不向き。
- 切断法は、複雑なトラスの中のある特定の部材に働く内力を知るのに向いている。
- どちらの方法も『切断した自由体の平衡条件を考える』のがポイント！
夢へ駆ける少女の姿に感涙！！
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか？」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい！」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanなら2/4までなんと3巻無料で読めてしまいます！まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです！
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
Contents
トラスとは
トラスとは下の絵のような構造体で、ポイントはすべての部材がピン接続されていることだ。
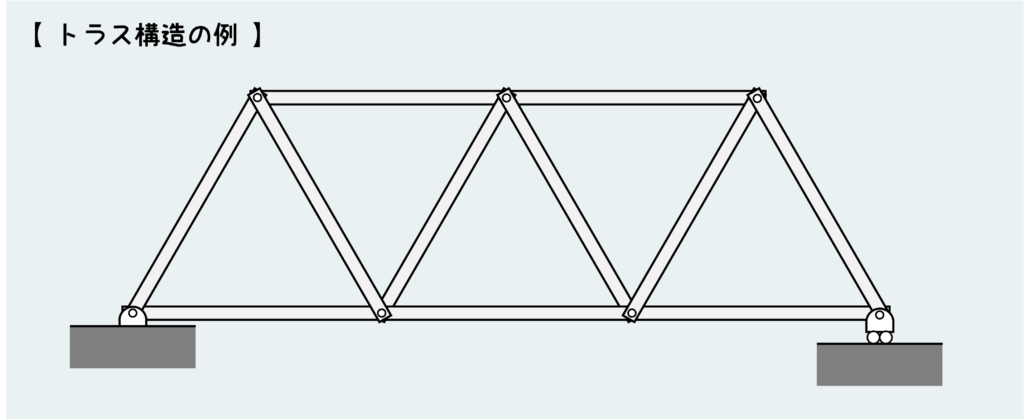
ピン接続というのは『部材同士が離れないように拘束している一方で、部材同士の回転は拘束しない』という特徴がある。これはつまりどういうことか言うと、『力を内力として伝えることができるが、モーメントは伝えられない』ということである。
これがピン接続の大きなポイントだ。
その結果、トラスを構成する部材には軸力（長手方向の力）しか働かないというめちゃくちゃ重要ポイントが生まれる訳だ。
少し詳しく説明しよう。
下の図のように、トラスからある部分の部材を切り出して考えてみる。
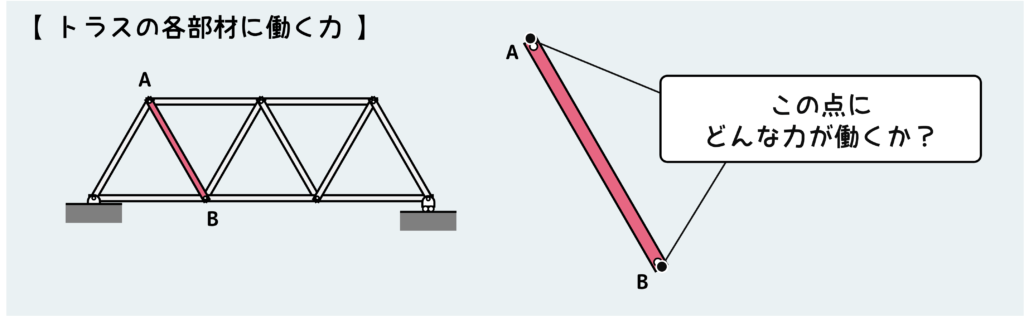
この部材の両端にはピンから内力が伝わってくるはずだが、さっき言った通り、ピンはモーメントを伝えることができないので、この部材の両端に書き込むことができる（つまり発生する可能性がある）内力は軸力とそれに垂直な方向の力だけだ。モーメントは書き込めない。
さあここでこの部材の平衡条件を考えてみよう。まず力の平衡条件が成り立つためには、両端にかかる軸力と垂直方向の力はそれぞれ同じ大きさで反対向きである必要がある。これで力は釣り合った状態になる。
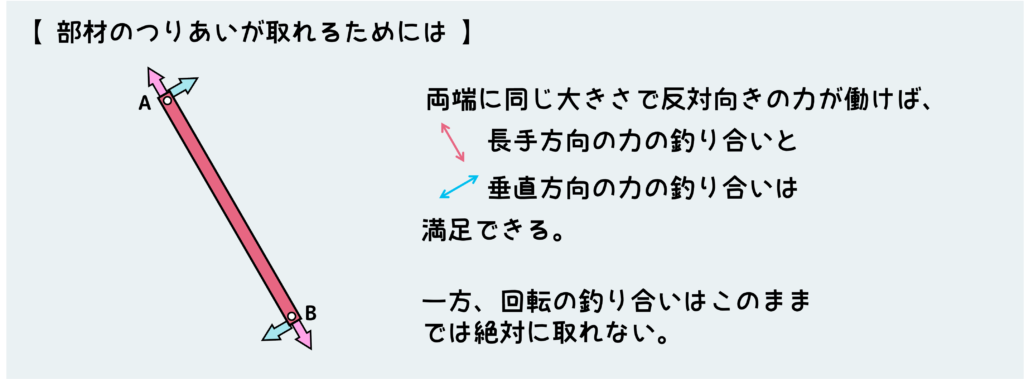
しかし、このままでは回転のつり合いが絶対に取れないことに気づくだろうか。軸力は回転に寄与しないのでこのままで大丈夫だが、垂直方向の力がどうしても回転の釣り合いをくずしてしまう。
力の釣り合いと回転の釣り合いを同時に満たすためにはどうしたらいいだろうか？答えは一つだ。
そう、垂直方向の力が”０”、つまり存在しなければいい。これ以外にこの部材の平衡条件が成り立つ術はない。
という訳で、トラスを構成する部材は必ず軸力のみを受ける状態になる。このことがトラス問題を考える上でめちゃくちゃ重要な前提となる。
絶対に軸力しか働かない！
一つ注意してほしいのは、これはトラスがピンで接続された構造体だから持つ特徴ということだ。これがピン接続ではなく剛接続で構成されるようなラーメン構造だと全く違う考え方が必要だ。
ラーメン構造については、またいつか説明したい。
軸力しか働かないおかげで、トラス構造は強いと言える。構成するひとつひとつの部材は細くても、全体として強い荷重を支えられる。
これはどういうことか？このことを理解するために、次のようなことを想像してみよう。
なんでもいいけど細い枝みたいなものを指の力で壊すことを考えてほしい。枝を引っ張って壊すことは相当なキン肉マンでない限りできない芸当だろう。だいたいの人は曲げて折ることで壊そうとするだろう。
指がかけることができる力（外力の大きさ）は変わらないはずだが、負荷形態（引張か曲げか）によって材料が受ける負荷（応力）は大きく変わってしまう。
つまり、『曲げ』というのは外力が小さくてもとても大きな応力を生み出すことができる負荷形態であり、材料にとってはなるべく避けたい状態である。
トラス構造は、ピン接続することで軸力しか働かない（曲げを受けない）状態にすることで壊れにくい構造になってる訳だ。
トラス構造は軸力しか働かないため強い！
例えば下図のように、長さ2Lの橋的なものでどんな応力が発生するか考えてみる。
左のものはトラス構造、右のものはただ長さ2Lの棒を渡しただけのものだ。左のトラス構造では、最大で引張力Pが働き、これによる引張応力は\(\displaystyle\frac{4P}{\pi d^2}\)である。一方右の構造では曲げが働き、これによる最大の引張応力は\(\displaystyle\frac{16PL}{\pi d^3}\)である。
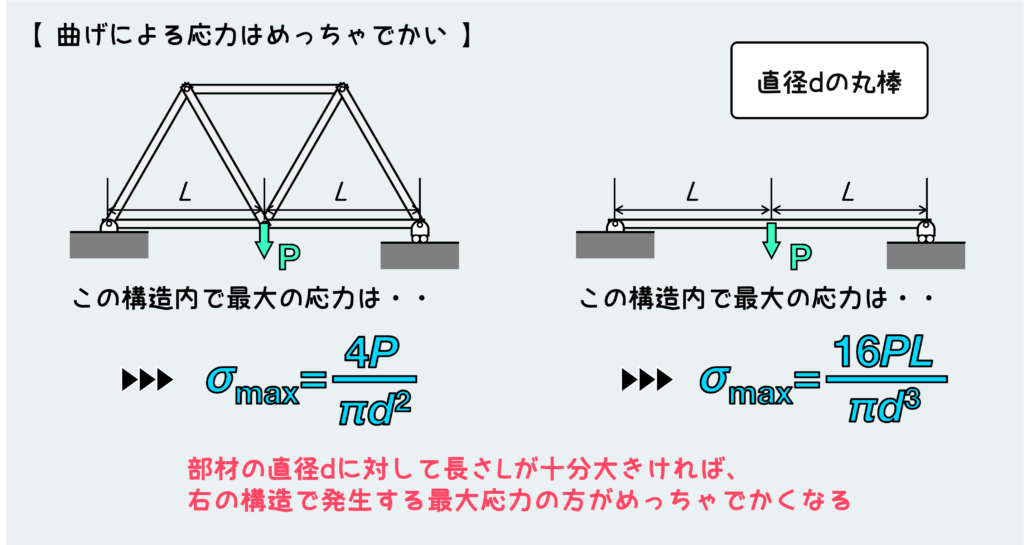
この部材の直径dに対して長さLが十分大きければ、右の構造に発生する曲げによる応力の方がトラス構造で発生する応力よりもとっても大きくなる。
このように、材料は多くの場合に曲げを受けるととたんに弱くなる。なのでなるべく曲げが発生しないような構造にすることは重要なことで、トラス構造にするのはその一つの手段な訳だ。
力の伝わり方（内力）を把握する
トラス構造において各部材に伝わる内力の大きさを把握する方法は２種類ある。
それが”節点法”と”切断法”だ。それぞれに以下のような特徴がある。
- すべての部材に伝わる力を明らかにできる。
- トラスのある点の変位を考えたいときには便利。
- トラスが複雑すぎると、平衡条件を考える数が膨大になり大変。
- トラス内のある特定の部材に働く力を知りたいときに便利。
- トラスがどんだけ複雑でも関係ない。
- 全部の部材の力や変形量を知りたいときには不向き。
上の特徴を踏まえて、使い分け方としてはこんな感じだ。
- トラスの中の特定のある部材に働く力を問われている時は”切断法”
- トラスを構成する三角形の数が２、３個の時は”節点法”で、４個以上の時は”切断法”
- すべての部材に働く力が知りたいときや、変形量を問われる場合は”節点法”
おおよそ上のような感じで使い分ければ良いと思うが、どちらの方法もちゃんと使えることが重要だ。
この後、やり方を丁寧に解説するので、しっかり身につけよう。
切断法のやり方と簡単な具体例
まず切断法のやり方だ。以下の手順に従ってやればOKだ。
まず初めにトラス全体を支点から切り離して、トラス全体の平衡条件から支点から受ける反力を決定する。支持方法に注目して、反力の種類を限定することが重要だ。
たとえばどこか特定の部材に働く力が知りたいとき、その部材を切断するようにトラス全体を切断する。このとき、中途半端な位置で切断するとやりにくいので、この部材とピンとの境界で切断するようにすると良い。
目当ての部材以外にもいくつかの部材を同時に切ることになると思うが、この切断した部分に内力を書き込む。このときのポイントは『各部材には軸力しか働かないこと』で、このことを意識して正しい方向に内力を書き込むことが重要。
切断したトラスの平衡条件から、Step３で書き込んだ未知の内力の大きさを決定する。
節点法よりもやってることはシンプルだと思う。節点法と違ってトラスの部材に伝わる力の全体像は分からないが、ある特定の部材に働く力を明らかにしたいときは切断法の方が速くて便利だ。
じゃあ簡単な例を解いてみて、解き方と切断法の利点について確認しよう。
下のような問題を考えてみよう。
この問題は部材の数がそれなりに多くて、これを節点法で解くのは少し面倒だろう。（できないことはないし、そこまで難しくはないけど、ただただ面倒だ）
変形に関する問題だったら、面倒でも各部材に働く力を一つ一つ求めていかなくてはならないけど、今回の問題のように特定の部材に働く力を聞かれているような問題であれば切断法を使えば簡単だ。
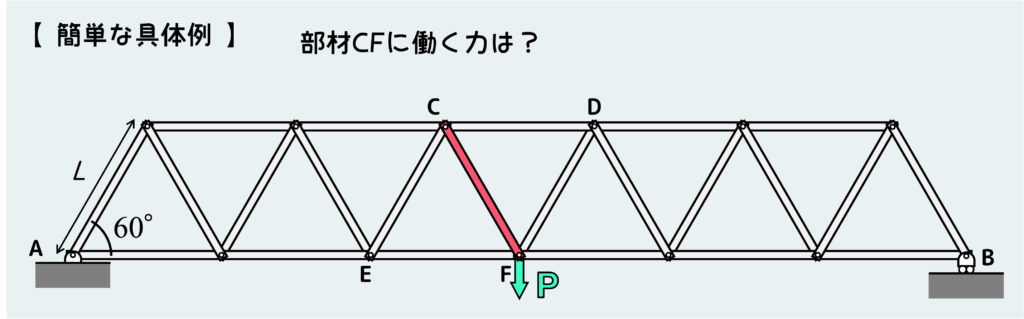
では、手順に従って解いてみよう。
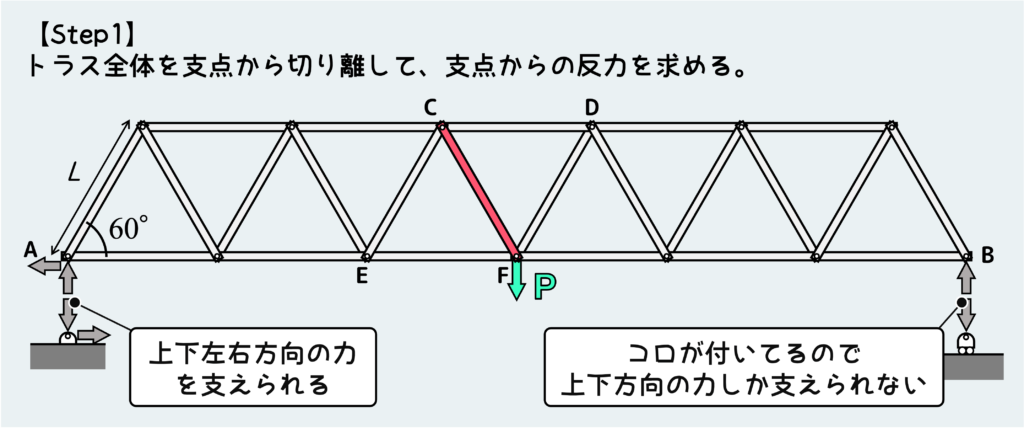
まずは支点からの反力を求めたいので、トラス全体を支点から切り離して、反力を書き込む。
この時注意したいのは、支持方法によって支点から受ける反力の種類が変わることだ。
左の支点Aではピン支持なので、上下方向の力に加えて左右方向の力も支えられる。なので、A点に書き込む反力は２種類（上下方向＆左右方向）になる。一方右の支点Bではコロが付いているので、左右の動きが拘束されていない。つまり左右方向の力を支えることができないので、この支点から受ける反力は上下方向の力だけである。
支持方法によって支点から受ける反力の種類が変わる。
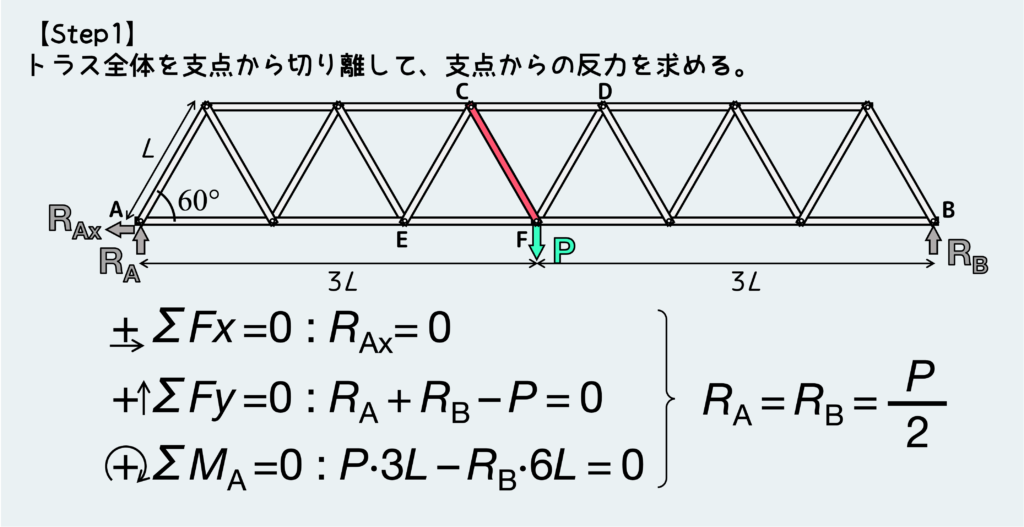
上記のことに注意して反力を書き込んだら、トラス全体の平衡条件からこれらの反力を求める。
各支点から受ける反力は下のように求めることができる。
これで切断法をやるための下準備が整った。
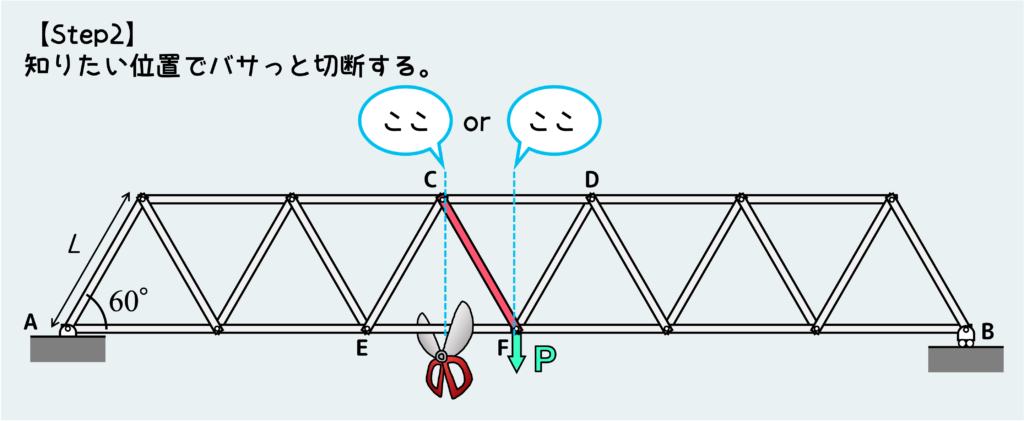
さて、ここから切断法のメイン部分になる。切断法では、今内力を知りたい部材のどこかで切断する必要がある。
部材中ならどこで切ってもいい、、、が、なるべく簡単に解くためには節目節目のところで切断するのが良い。なぜなら、このあと回転のつり合いを考える際に『距離』が必要になるが、この距離を簡単に見極めるためには分かりやすいポイントを切断位置にした方がやりやすい。
そうは言っても切り方は色んなパターンがあるが、ここでは下図の左の位置（はさみの絵が描いてある青線）で切断したパターンで解いてみる。
切断したら、今切った部材の断面に内力を書き込む。ここでのポイントは、トラスの大きな特徴である『部材に働く内力は軸力のみ』だ。
この特徴に従うと、自然に書き込む内力の方向は決まってくる。切断した部材の長手方向に沿うように各部材に働く内力を書き込んでいく。
厳密には引張か圧縮かは現時点では分からない。なのでひとまず全部引張だと仮置きして、内力を書き込んでいく。
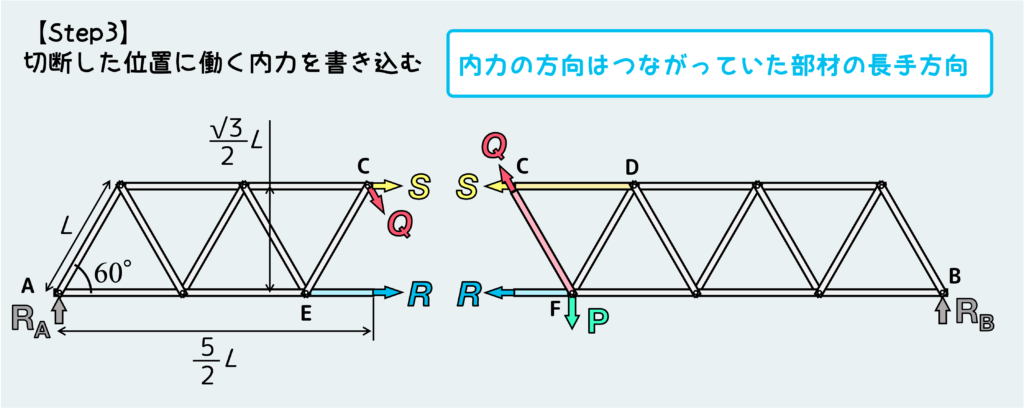
内力を書き込んだら、切断したトラスの平衡条件から未知の内力（Q、R、S）を求める。
切断したトラスは左側と右側の２つがあるが、どちらの平衡条件を考えても同じ答えが出てくる。なので、簡単そうな方でやれば良い。今回は左側のトラスの方が簡単そうなので、左側のトラスの平衡条件を考えていく。
すると、下図のように平衡条件式を立てることができて、未知の内力Q、R、Sが求まる。
ここでSに関しては（マイナス）が付いているが、これは最初の仮置きとは逆向きという意味だ。最初の仮置きはすべて引張で仮定したので、部材CDに働く内力は圧縮だったということが分かる。
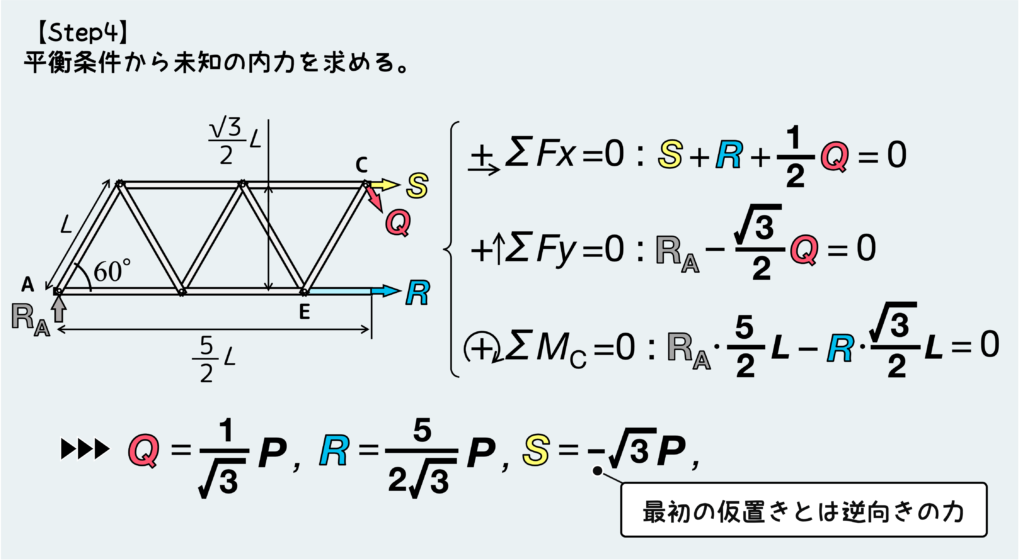
明らかになった情報を整理すると、下のようになる。
これで、元々の問題で聞かれていた部材CFに働く力は\(\displaystyle\frac{P}{\sqrt{3}}\)の引張力だということが分かる訳だ。
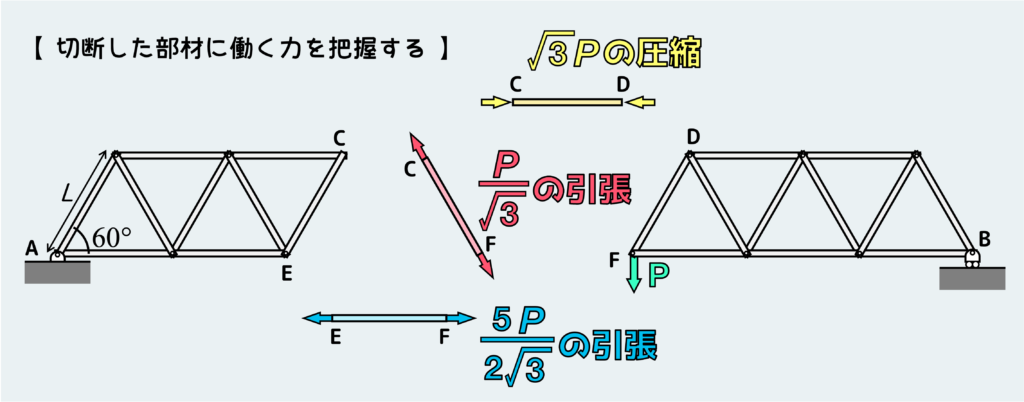
節点法と比べてかなりシンプルだと思う。
ただ、上で説明した通り、節点法の方が向いている場合もあるので、両方のやり方と長所・短所をしっかりと理解して使い分けることが重要だろう。
節点法と切断法の両者をよく理解して使い分けることが重要！
まとめ
トラスに伝わる力を切断法を使って考える方法について説明してきたが、理解できただろうか。
トラスの問題はテストでもよく出る問題だと思うので、今回の記事をよく読んでしっかりと身につけてほしい。
節点法について知りたい人は以下の記事を合わせて読んでほしい。
材料力学 10分で絶対分かるようになるトラス問題（節点法による力の伝わり方編）【Vol. 3-4】
また、トラスの変形問題については次の記事で説明したいので、ぜひ読んでみてほしい。
材料力学 10分で絶対分かるようになるトラス問題（変形量編）【Vol. 3-6】
- トラス部材には軸力しか働かない。これのおかげで強い構造体にできる。
- 各部材に働く内力を明らかにするには節点法と切断法がある。
- 節点法はすべての部材に働く力を明らかにしていき、ある点の変位を知りたい場合に使える。あまりにも複雑なトラスの場合は不向き。
- 切断法は、複雑なトラスの中のある特定の部材に働く内力を知るのに向いている。
- どちらの方法も『切断した自由体の平衡条件を考える』のがポイント！
研究者を志す者 必読！！
全8巻完結
こんなにも知的探究心を刺激される漫画があったとは！
真理のために命をかけた先人たちの物語。
この作品は、現役研究者である私・ぽるこが衝撃を受けた作品として、特に研究者およびこれを志す者には強く本気でオススメします。今ある常識を疑う心、誰に何を言われようと真理を追求する姿勢に触れ、心が動くこと間違いありません。
私自身、世界のトップ研究者だった師匠によく言われた言葉を思い出します。“目の前の現象に楽な答えを持ち出し、疑うことをやめ、真理の追求という困難な道から逃げていないか！？”
本作はこういった研究者の気概なるものを感じる、必読の価値ある一冊です。全8巻ですでに完結していますし比較的手軽に一気読みできます。気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！