材料力学《全員必見・超重要》自由体の考え方（トラスの問題）【Vol. 1.2-3】

このブログでは「プロモーション」が含まれています。

今回の記事は自由体の考え方の具体例第３弾ということで、トラスの問題だ。

自由体の考え方とはつまり、力の伝わり方を把握するということである。この記事ではトラス構造の力の伝わり方の考え方を簡単に紹介したい。では早速本題に入ろう。

その他の具体例は以下の通り。

2021年5月13日材料力学　《全員必見・超重要》自由体の考え方（引張・圧縮を受ける棒）【Vol. 1.2-1】

2021年5月13日材料力学《全員必見・超重要》自由体の考え方（色んな支持方法）【Vol. 1.2-2】

2021年6月9日材料力学《全員必見・超重要》自由体の考え方（異種材料・別部品）【Vol. 1.2-4】

2021年6月22日材料力学《全員必見・超重要》自由体の考え方（曲げ・ねじり問題）【Vol. 1.2-5】

自由体の基礎について確認したい人は下の記事を読んでほしい。

2020年10月13日材料力学　《全員必見・超重要》自由体の考え方の基礎【Vol. 1.1】

この記事でわかること

トラス構造とは、各部材同士がピン接続され、三角形の組合せで構成される構造体
トラス構造の各部材には軸力（部材の長手方向の力）しか働かない
節点と部材を全部バラバラにして、節点の平衡条件から各部材に働く力を決定する
節点の平衡条件を考えるときは、ベクトル和の考え方を利用すると良い

夢へ駆ける少女の姿に感涙！！

メダリスト / つるまいかだ

12巻連載中

「司先生は…っ　　わたしが世界一になりたいって言ったら手伝ってくれますか？」

2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。

「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい！」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。

ebookjapanなら2/4までなんと3巻無料で読めてしまいます！まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです！

Amazonで探す

楽天で探す

ebookjapanで読む

私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！

この記事を読む

Contents

トラスってどんな構造？
- トラスって何？
- トラスの特徴
トラスにおける力の伝わり方
まとめ

トラスってどんな構造？

トラスって何？

Image by Kanenori from Pixabay

トラス構造は身近な所でも見ることができる。一番見かけるのは橋だろう。あとは何ちゃらタワーとか。。

こういう三角形を組み合わせたような構造で、各部材（三角形の各辺の部分）同士はピン接続されている。三角形の組合せにすることで強度を持った構造を実現している。

材料力学でももちろん登場する訳だが、わりと苦手な人が多いのではないだろうか。この記事では、力の伝わり方の考え方を簡単に紹介する。特徴をちゃんと押さえれば別に難しいことはないので、ぜひ最後まで読んでみてほしい。

トラスの特徴

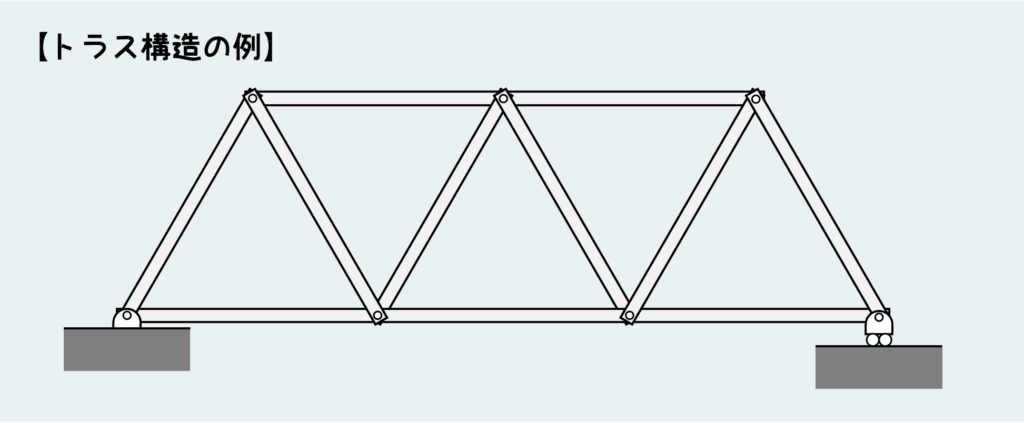
材料力学で登場するトラスの例はこんな感じだ。複数の部材がピンで接続され、三角形の組合せを構成している。トラス構造のポイントはずばり、各部材が「ピンで接続されている」ことだ。

ピンで接続されているということは、前の記事でも説明したように回転の動きを支えられないので、モーメントを伝えることができない。

では、このことを踏まえた上で、各部材にどんな風に力が伝わるか考えてみよう。

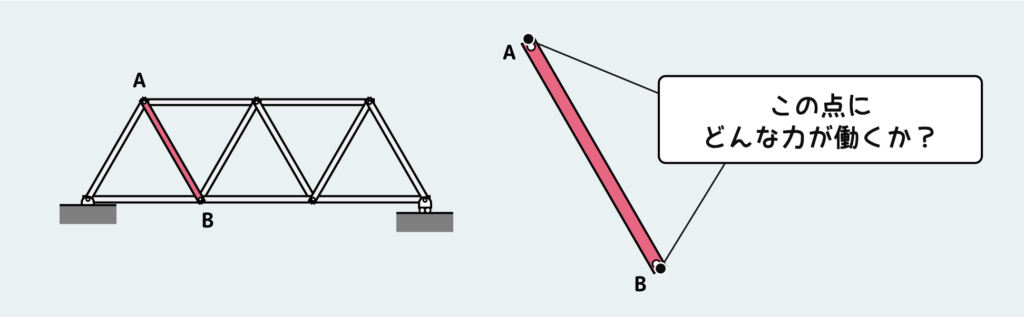
トラスの中から１本の部材ABを抜き出してきて、これにどういう力が伝わるか考えよう。

まず、この部材は元々ピン接続されていたA点とB点で切り離して自由体として取り出してきたものなので、このA点とB点以外の表面部分は自由表面であり、力が働くことはない。ではどこに力が働くか？

もちろん、A点とB点だ。A点とB点には２種類の力、つまり「部材の長手方向に向いた力」と「これに垂直な力」が働く可能性がある。下図のような状態になる訳だが、結論から言ってこの状態だと釣り合いが取れない。

長手方向および垂直方向の力の釣り合いは取れる。同じ大きさで反対向きの力がA点とB点に働けばいいだけだからだ。一方、回転の釣り合いはどうがんばっても取れない。部材に垂直方向の力がモーメントとして働くので、回転の釣り合いを取るためには、それを打ち消すようなモーメントがA点やB点に働かないといけない訳だ。

しかしさっき言ったように、A点・B点はピン接続なので、モーメントは発生し得ない。つまりこのままでは、絶対に平衡条件を満たすことができない。じゃあどうなれば平衡条件が成り立つかというと、垂直方向の力がなくなれば良いわけだ。そうなれば、長手方向・垂直方向の力の釣り合いと回転の釣り合い、すべての平衡条件が成り立つ。

すなわち結論はこうだ。トラス構造の各部材（両端ピン接続の部材）には、長手方向の力（軸力という）しか働くことができない。

これがトラスの大きな特徴だ。トラスを構成する各部材には軸力しか働かない。このことをよく分かっていれば、トラス問題の力の伝わり方を理解できるだろう。

ピン接続だとモーメントが働かない理由がよく分からない人は、支持方法によって発生する力が変化することを下の記事で説明しているので、ぜひ読んでみてほしい。

材料力学《全員必見・超重要》自由体の考え方（色んな支持方法）【Vol. 1.2-2】

POINT

トラスを構成する部材には軸力しか働かない。

トラスにおける力の伝わり方

ではトラスの大きな特徴をつかんだ上で、簡単な具体例を見ていこう。ものすごく丁寧に順序を踏んで説明するので、分かってる人は流し読みで十分だろう。

上図のような簡単な例を通して、トラス構造の力の伝わり方を理解しよう。

まずトラス問題のアプローチは、部材と節点をすべてバラバラに切り離して自由体図を描くことから始まる。

上図のように節点と部材を全部バラバラに切り離す。これらの点と部材すべてが自由体として平衡条件を満たす必要がある。

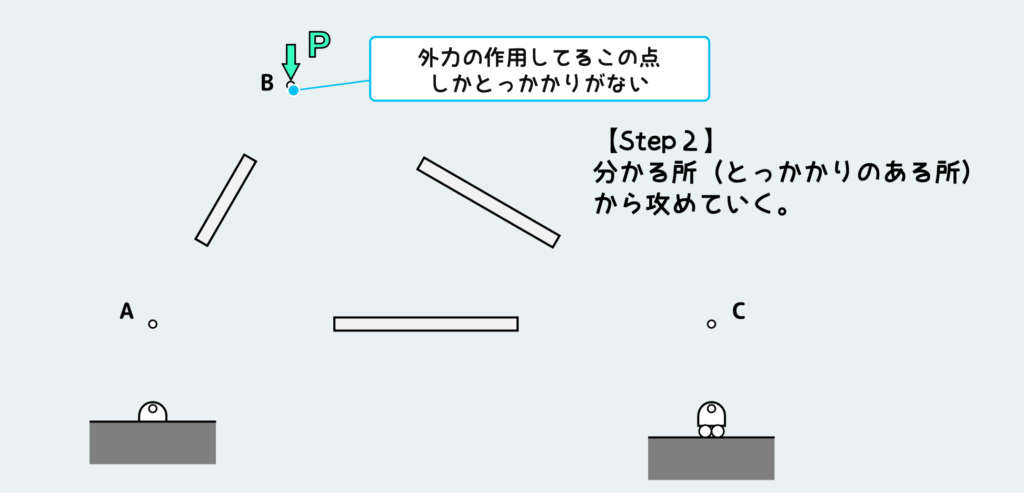
で、どこから考えるかというと、分かる所から攻めていくのがセオリーだ。この場合は、外力が作用しているB点の釣り合いから考えないといけない。というかそれ以外の自由体については、とっかかりがなくて現時点では何も分からない。

てことでB点の釣り合いから考えよう。

節点の平衡条件を考えるときには、回転モーメントの釣り合いを考える必要はない。なので、力の釣り合いさえ取れれば良い。こういう場合のポイントは「ベクトル和の考え方」を使うことだ。

ベクトル和とは、力をベクトルとして図の上で繋げて描いていき、最終的に行き着く所が全部のベクトルの和を表しているという考え方だ。力が釣り合っているためには、力を全部足し合わせたベクトル和が “0” である必要があり、つまり全部のベクトルを繋ぎ合わせていき元の出発点に戻ってくる。

（※ 節点に働く力が４つ以上になると、場合によってはベクトル和を考えるのが難しくなることがあるので、そのときは素直に水平方向・垂直方向の２つの力の平衡条件式を立てて、連立方程式を解こう）

部材には軸力だけが働くので、このB点が部材AB・BCから受ける力の方向は決まっている。あとは、ベクトル和が”0″になるような図を描いて、AB・BCから受ける力の大きさを決定する。

上図のようにベクトル和を描けるので、B点に働く力が決定できる。

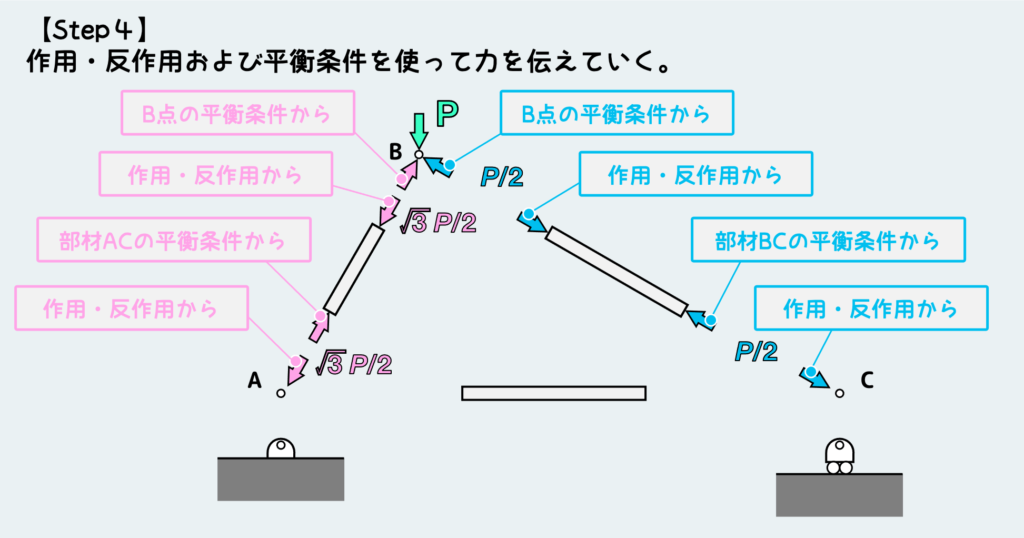
このB点に働く力は元々繋がっていた部材AB・BCから受けた力なので、「作用・反作用の法則」から同じ力を部材の方も受けることになる。さらに、部材の平衡条件を満たすために、部材の反対側にはまた同じ力が働く。そして、この力は部材の先の節点から受けた力なので、作用・反作用の法則から同じ力が節点の方にも働くことになる。

ここまで来たら次の節点の力の平衡条件を考えよう。A点とC点のどちらから考えればいいか迷うかもしれないが、支持方法に注目すればこの迷いは解決する。A点はピン支持、C点はピン＋コロになっている。

A点はピン支持なので、縦横２方向の反力を受ける。それに加えて部材ACからも力を受ける。つまり現時点では３つの未知の力が働いていて、力の平衡条件式２つでは決定できない。（ちなみにベクトル和の考え方は、力の平衡条件式２つを同時に使ってるようなもんだ）

一方、C点はコロが付いてるので、支点からは縦方向の反力のみを受ける。C点も同じく部材ACからも力を受けるので、未知の力は２つになる。という訳で、C点の釣り合いから先に考えるべきだ。

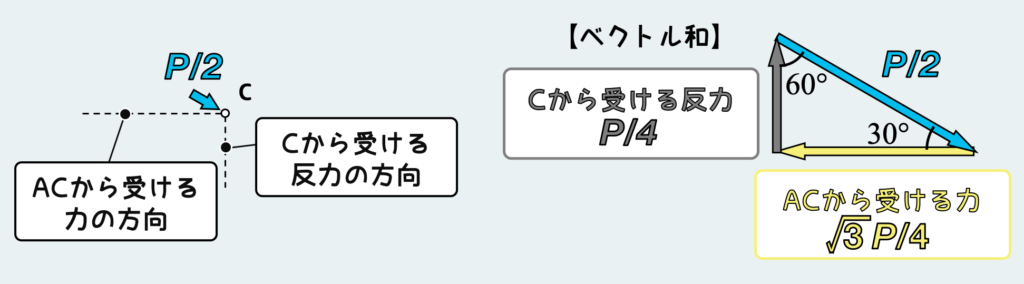
支点から受ける反力が縦方向のみであることに注目して、B点のときと同じようにC点に関する力の釣り合い、つまりベクトル和＝0 を考える。C点のベクトル和を考えることで、部材ACから受ける力も決定する。

部材ACから受ける力が分かれば、作用・反作用から部材ACがC点から受ける力も分かる。さらに平衡条件、作用・反作用の法則を使って力を伝えていくと、下図のように、このトラス構造全体の力の伝わり方の全貌が見えてくる訳だ。

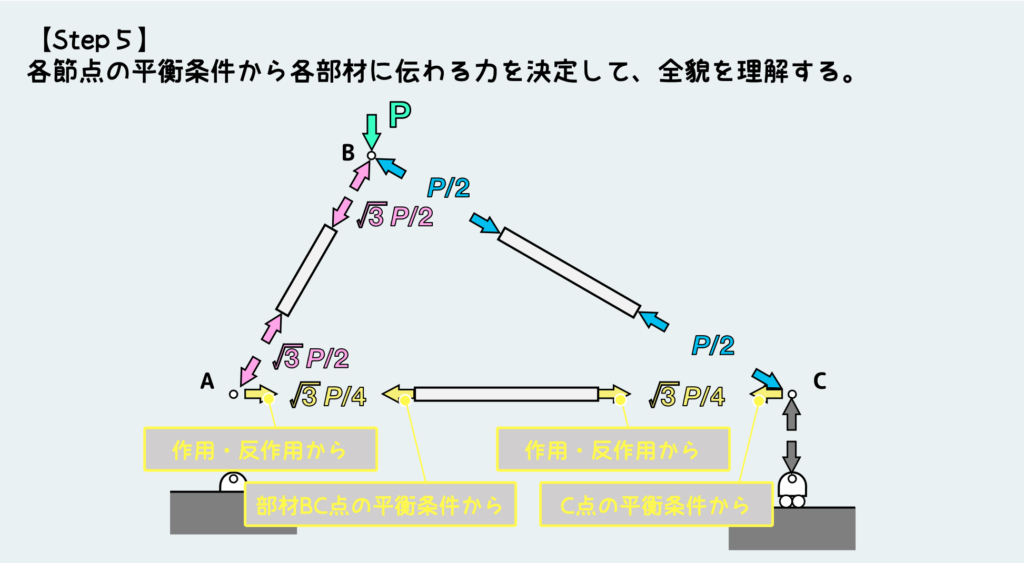
最後にA点の平衡条件を考えなくていいのか？と言うと、これは別に考える必要はない。各部材に伝わる力はもう決定できたので、これらを使ってトラスの変形を考えることも応力を考えることもできる。もちろんA点から受ける反力を知りたいのであれば、A点の平衡条件まで考える必要があるが、まあ普通そんなこと聞かれないだろうと思う。