前の記事で、自由体の考え方の意味と使い方について基本的なことを説明した。これからいくつかの記事で、色んなパターンの問題を見ていくので、さらに自由体を使いこなせるようになってほしい。
今回から全部で５つの事例を紹介する。長くなるので、気になるところだけを読んでもらえば良い。もちろん全部読む気力がある人はぜひ全部読んで理解を深めてほしい。
この記事では、【引張・圧縮を受ける棒】について解説する。
その他の例は以下の通り。
材料力学《全員必見・超重要》自由体の考え方（色んな支持方法）【Vol. 1.2-2】
材料力学《全員必見・超重要》自由体の考え方（トラスの問題）【Vol. 1.2-3】
材料力学《全員必見・超重要》自由体の考え方（異種材料・別部品）【Vol. 1.2-4】
材料力学《全員必見・超重要》自由体の考え方（曲げ・ねじり問題）【Vol. 1.2-5】
自由体の基礎について確認したい人は下の記事を読んでほしい。
材料力学 《全員必見・超重要》自由体の考え方の基礎【Vol. 1.1】
- 内力は、必ず自由体を切り出してから断面に描き込む
- 単純な引張・圧縮を受ける材料の内部には、どの断面を見ても一定の引張もしくは圧縮の内力が伝わる
- 複数の引張・圧縮外力を受ける材料は、単純な引張・圧縮を受ける材料の組合せとして考えることができる
- 材料内部の内力の伝わり方を把握することが第一歩であり、これにより材料の応力や変形を考えることができる
夢へ駆ける少女の姿に感涙！！
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか？」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい！」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanなら2/4までなんと3巻無料で読めてしまいます！まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです！
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
Contents
引張・圧縮を受ける棒
この記事では下記のような「引張・圧縮を受ける棒」の問題を考えることで、基本的な自由体図の描き方を習得しよう。
片側が壁につながった棒の途中の点に外力が作用している。このときの①壁から受ける反力と、②AB・BC・CD各部の負荷状態について考える。
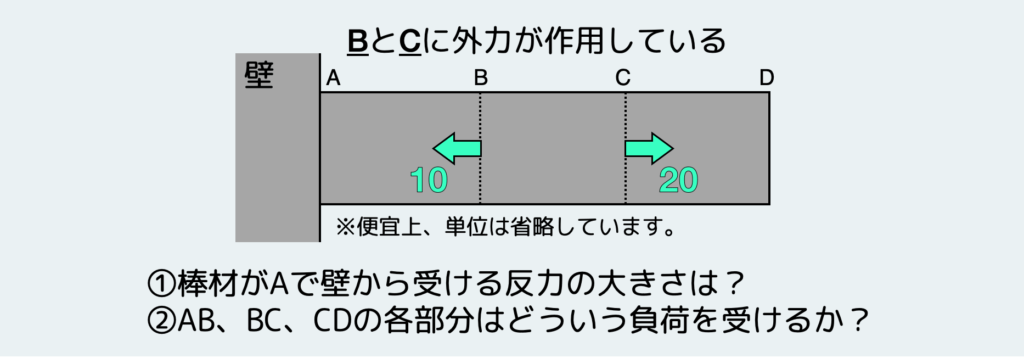
まずはA点での壁から受ける反力を考えてみよう。
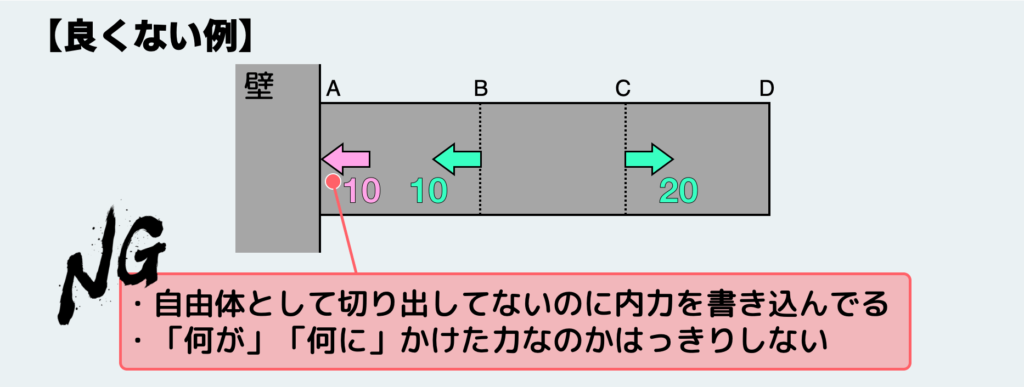
反力も一種の内力なので、自由体を切り出さずには決して見えない。なので、上の図のように自由体を切り出さずに反力を書き込むのは良くない。
確かに書き込まれた力の合計はつり合ってはいる。だが、決定的に良くない点がある。それは、このままでは「何が」「何に対して」かけた力なのかはっきりしないことだ。
このような簡単な問題であれば確かにこのやり方で乗り切れるかもしれないが、少し複雑になってくると、こういうやり方をしていてはきっと混乱してしまうだろう。
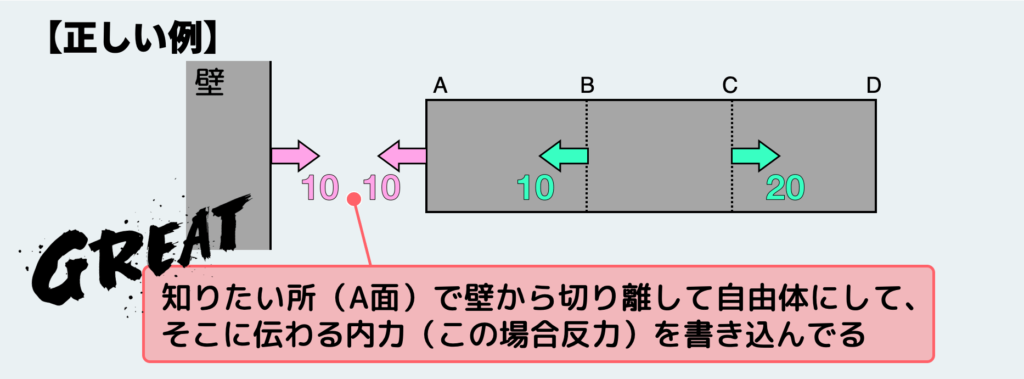
正しくは、上図のようにしっかりと知りたい場所（この場合は反力が知りたいので壁と接続されたA面）で切断し、自由体として切り出してから、この切断面に内力を書き込まなくてはならない。
これが基本だ。材料を切らずに自由体を描いたつもりになっている人は本当に多いので、思い当たる人はまずこの基本に立ち戻ってほしい。
次にこの材料内部の負荷状態について考えよう。まず試しにBC間の適当なところで切って、ここに伝わる内力を考えてみる。
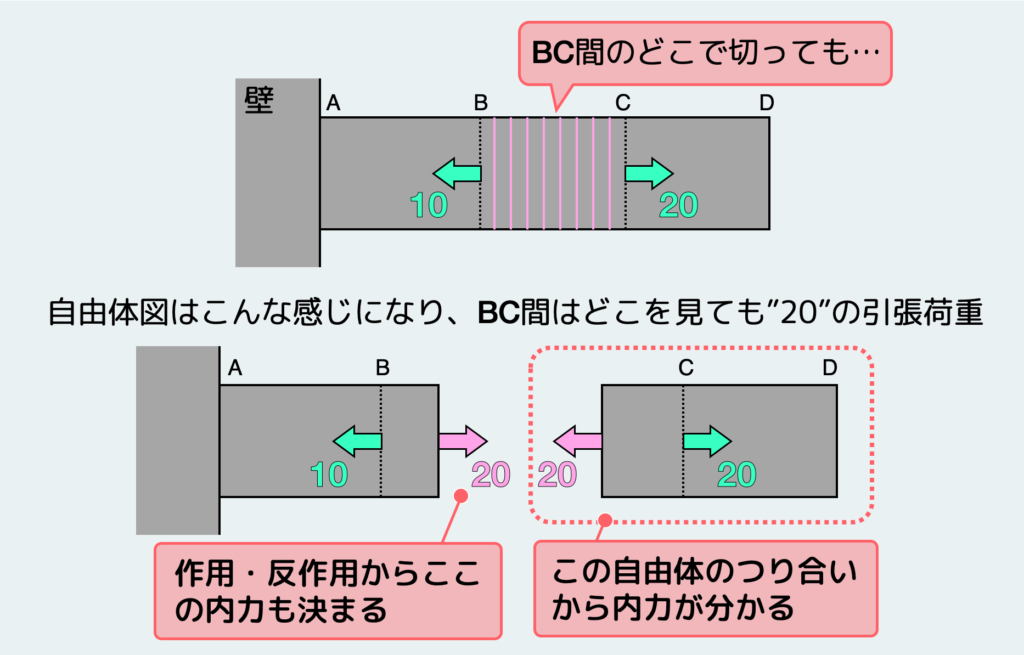
すると、実はBC間のどこを切断しても、できる自由体図は本質的に変化しないことがわかるだろう。つまり、BC間のどこで切ってもその断面に作用する内力は”20”の引張荷重となる。
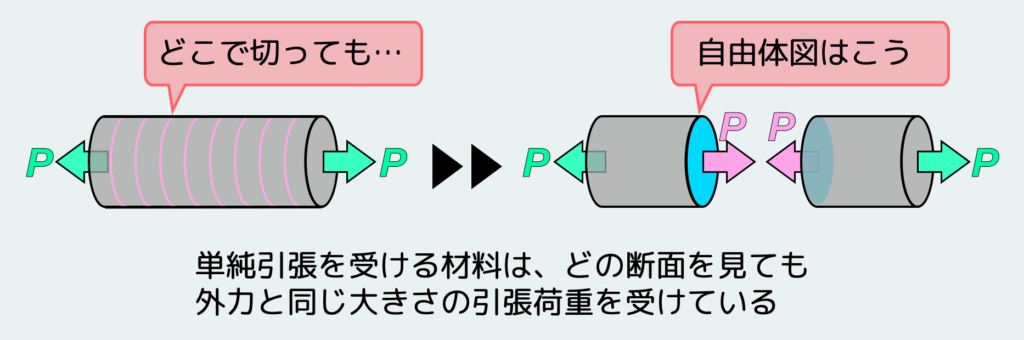
ここで、前回の記事で説明したことを思い出そう。両端に引張荷重Pを受ける棒の内部には、端から端まで一定の引張荷重（外力と同じ大きさ）が働いている。BC間も同様に端から端まで一定の引張荷重が伝わっており、これと等価な状態になっている訳だ。
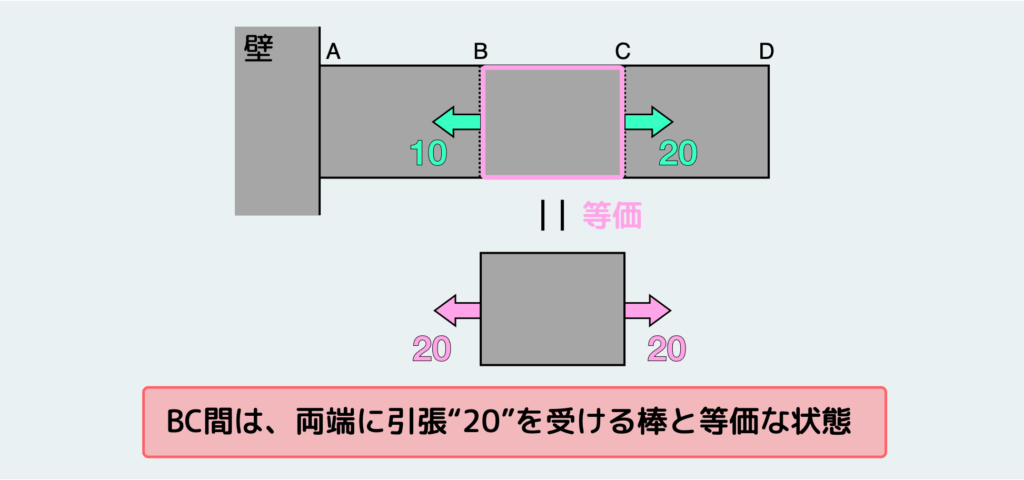
すなわち、BC間は両端に引張荷重”20”を受ける棒と等価な状態という訳だ。では次にAB間、CD間の内部もどういう内力が伝わってるか考えよう。
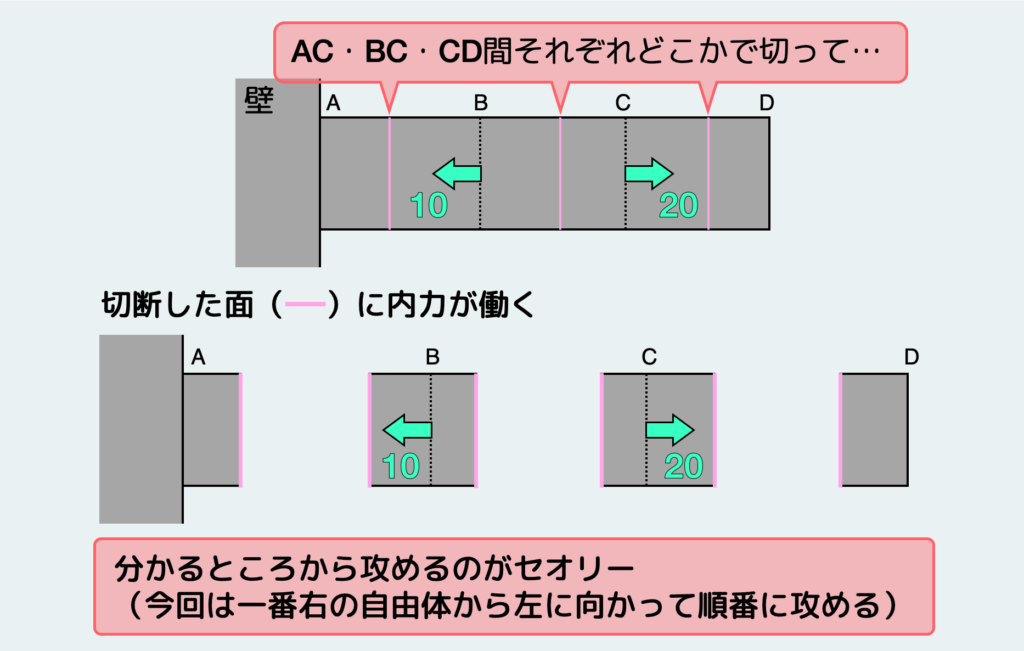
今回はAB間、BC間、CD間それぞれ同時に、適当なところで切って自由体図を描く。複数の自由体が出来上がるが、これらの自由体が平衡条件を満たすように内力が働く必要がある。こういう複数の自由体の釣り合いを考えるときは、分かるところ（未知の力が少ないところ）から攻めていくのがセオリーだ。この問題の場合は一番先端の自由体の釣り合いから攻めていく。
一番先端から、平衡条件と作用・反作用の法則を駆使して、順番に未知の内力を決定していくと上図のようになる。
BC間の内力を考えた時と同様に、AB間、CD間も切る位置が変わってもそこに伝わる内力は変化しない。つまり、AB間は一定の引張荷重”10”が作用しており、CD間はどこを見ても無負荷の状態だと分かる。
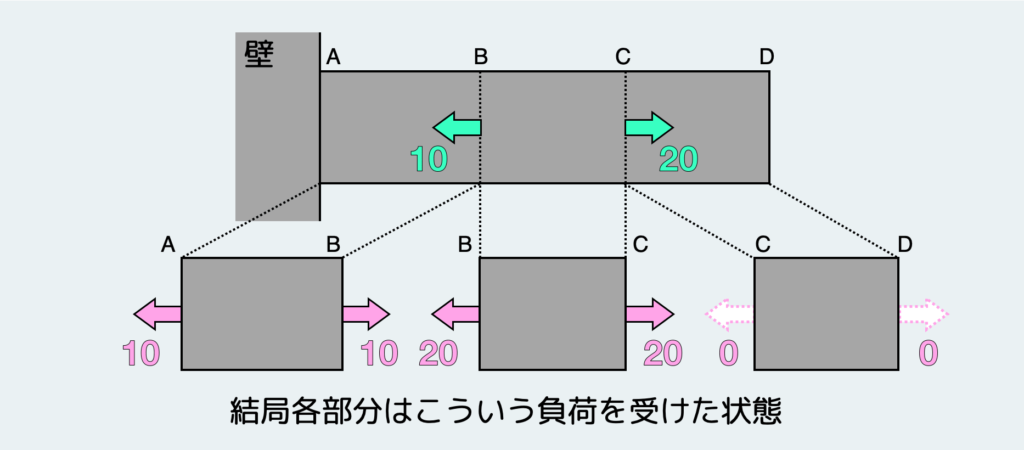
そうすると、BC間を考えた時と同じ理屈で、AB間は両端に引張”10”を受ける棒と等価な状態であり、CD間は負荷を受けていない棒と同じ状態だと言うことが分かる訳だ。
結論としては、この構造体は「引張”10”を受ける棒」「引張”20”を受ける棒」「無負荷の棒」の３つのパーツから構成されているということが言える。
材力の問題では、このように「どこからどこまでどういう内力が伝わってるか」を正確に把握することが最初の一歩で、これができれば次のステップとして、各部分に働く応力の大きさや変形量（伸びや縮み）を計算することができるようになる。
上の説明でもう十分だとは思うが、やや腑に落ちない人もいるかもしれない。そんな人のために別の、もう少し直接的な解説をしてみよう。
AB、BC、CDがどういう負荷（内力）受けるか知りたいので、まさにAB、BC、CDをそのまま自由体として取り出してみる。下の図を見てほしい。
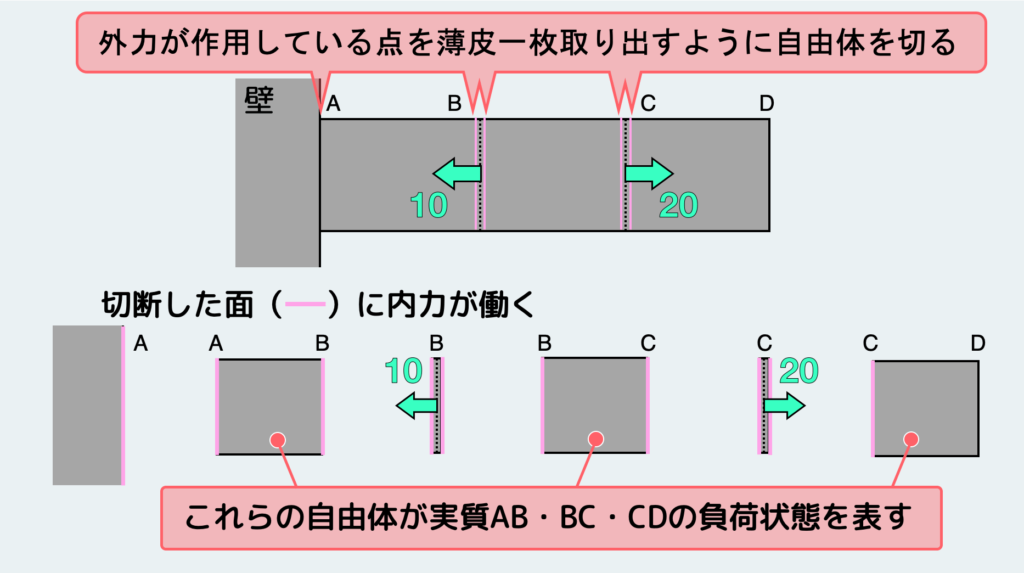
Bの面、Cの面でバサッと切りたくなるが、そうすると外力をどこに描けばいいのか混乱してしまうかもしれないので、外力を含まないように外力が作用している点のすぐ左右で切ることを考えよう。
すると、上図のようにAB、BC、CDと外力を含むような薄皮一枚の自由体２つの合計５個の自由体を取り出せる。
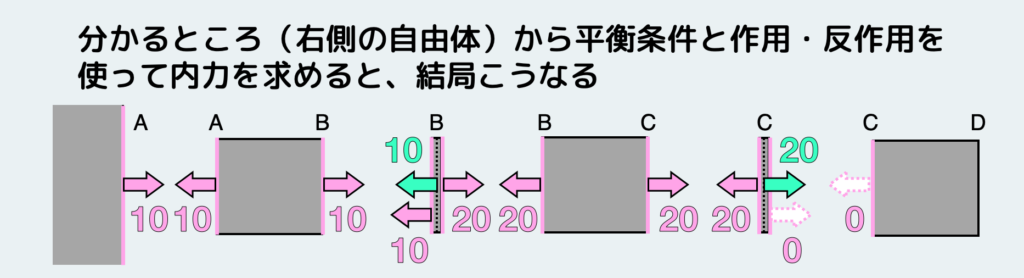
あとは、やはり先端の方から順番に、平衡条件と作用・反作用の法則を使って内力を決定していく。そうすると結果的には、（当たり前だが）上で説明したときと同じ結論が得られる。
まとめ
この基本的な問題を考えることで、自由体の考え方、描き方が分かったはずだ。
繰り返しになるが何回言ってもいいぐらい重要だから、もう一度次のポイントをしっかり理解してほしい。これを分かった上で他の例も見てみよう。一通り理解できたときには、材力の根幹の重要部分は抑えたことになるだろう。
- 内力は、必ず自由体を切り出してから断面に描き込む
- 単純な引張・圧縮を受ける材料の内部には、どの断面を見ても一定の引張もしくは圧縮の内力が伝わる
- 複数の引張・圧縮外力を受ける材料は、単純な引張・圧縮を受ける材料の組合せとして考えることができる
- 材料内部の内力の伝わり方を把握することが第一歩であり、これにより材料の応力や変形を考えることができる
理工系人材必読の超おもしろ漫画！！
連載中
『まずは音を出して 音を出さなきゃ音楽は始まらないのよ』
今、忘れかけていた夢への一歩を踏み出す！
いつの間にか多くの人は昔描いた夢のことを忘れてしまう。『宇宙兄弟』は“夢を追うのに遅すぎるなんてことはない”ということを教えてくれます。キャリアや進路に悩むすべての人の背中を押してくれる言葉にあふれている『宇宙兄弟』は多くの社会人や大学生から大絶賛されています。
宇宙開発や飛行士の活動をリアルに描く本作は、理工系の人の知的好奇心を刺激し、未知の問題へ向き合う姿勢を学べる必読書と言っても決して過言ではありません！
ebookjapanなら3巻まで無料で読めるので、気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
