前回の記事（材料力学 【kgf】から【N】への変換など単位のキホンその１【材力 Vol. 0.1】）に引き続き、材料力学で使う単位について説明したい。今回は、モーメント、応力、ひずみについてだ。応力は材料力学で初めて扱うもので、はじめは難しく感じるかもしれないが、避けては通れないのでがんばって理解してほしい。
- 単位をしっかり理解して自由自在に使いこなそう
- モーメント：（N・m）
- 応力：（MPa）=（N/mm2）
- 垂直ひずみ：単位なし、せん断ひずみ：（rad）
Contents
材料力学で登場する単位たち
モーメントは物体を回転させようとする負荷のことで、「力」×「支点からの距離」で表される。単位は（N・m）を使うことが多い。「力」の単位が（N）で、「距離」の単位が（m）というわけだ。
ただし、いろんな公式にモーメントを入れるときは（N・mm）に変換してから代入するのがオススメだ。モーメントの単位を（N・m）から（N・mm）に変換するときは、数値を1000倍したら良い。つまり、1（N・m）= 1000（N・mm）となる。
ねじりの問題を考えるときは、トルクというのが出てくるけど、これもモーメントの一種だ。単位の考え方もモーメントと同じように考えれば間違いない。
応力というのは、力を受けた物体にかかる負荷の大きさを表したものだ。負荷の大きさを表すのであれば「力」でもいいような気がするが、そういう訳にはいかない。材料にかかる負荷の大小は、単純に「力」だけで判断できないからだ。
応力ってなんだかわかりにくいんだよねー。
具体例を見た方が早いだろうから、下の絵を見てね。
下の絵のように、直径10 cmの鉄製丸棒と直径5 mmの同じく鉄製丸棒の両方に1 tonの車をぶらさげた状態を考えてみよう。丸棒にかかっている「力」はどちらも1000 kgf（10000 N）だけど、どうみても5 mmの丸棒の方がしんどい。
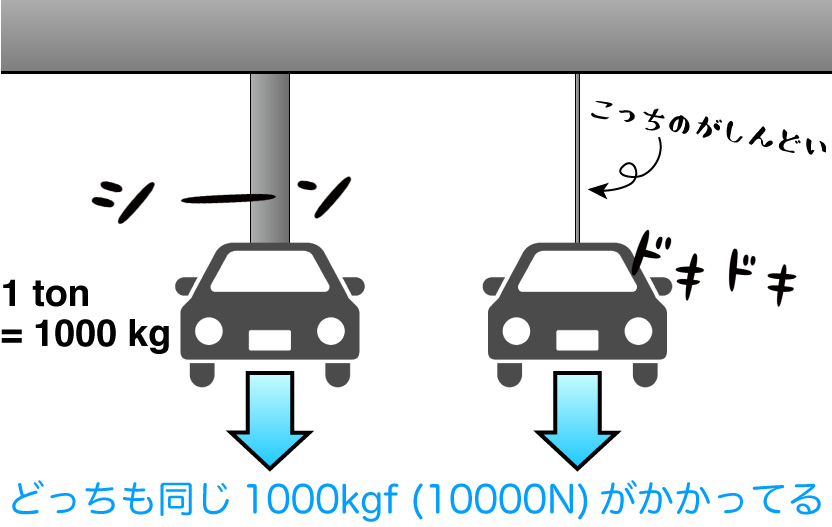
このように、同じ力を受けていたとしても、材料が受けている負荷の程度は同じにはならないから、負荷の大きさを評価するためには、「力」だけではなく部材の「サイズ」も考慮した物差しが必要になる。それが「応力」ということだ。
つまり、応力というのは、サイズが違う物体でも負荷の程度を比べられるようにしたもので、作用している力を物体の断面積で割ったものである（難しい言い方をすると、単位面積当たりに作用している力の大きさを表している）。
「力」を「面積」で割ったものなので、応力の単位は（N/m2）や（kgf/mm2）となる。しかし、（間違いではないが）実際にはあまり使わない。代わりによく使うのは（MPa）だ。
材料の主な機械的性質として降伏応力や引張強さがあるが、これらも通常は（MPa）を用いて表すことが多い。材力の問題では、与えられた降伏応力をもとに安全かどうかを判断したり、材料に負荷できる最大の荷重を求めたりするため、応力の計算は（MPa）を使えるようになるのが大切だ。
応力には【垂直応力】と【せん断応力】の２種類があるが、どちらも単位は（MPa）だ。
応力を正しく扱うことは材料力学においてすごく重要だ。応力について詳しく解説した記事も書いているので、ぜひ下のリンクを読んでみてほしい。
材料力学 応力とは？10分で完全に理解できる 基本かつ超重要な解説【材力 Vol. 2-1】
（Pa）というのは圧力の単位として見たことがあるだろう。圧力も応力と同じで、単位面積当たりにどれだけの力が作用しているのかを表したものだ。1（Pa）= 1（N/m2）で、M（メガ）というのは106という意味だから、1（MPa）= 1000000 （Pa）= 1000000（N/m2）ということになる。
さらに（mm）のm（ミリ）が10-3であることを合わせると、1（N/m2）= 0.000001（N/mm2）となるため、結果的には1（MPa）= 1（N/mm2）となるわけだ。
この関係性はいろいろな問題を解く上でものすごく便利なんだけど、どんな風に便利なのかは次の記事で詳しく説明することにして、ここではこの関係式だけは覚えていてほしい。
1【MPa】= 1【N/mm2】
材料力学 公式を正しく使い、計算ミスを減らすコツ【材力 Vol. 0.3】
垂直ひずみというのは変形量を表すもので、元の長さに対してどのくらい伸びたか（もしくは縮んだか）を割合で表したものだ。
「伸び もしくは 縮み」÷「元の長さ」で計算できる。
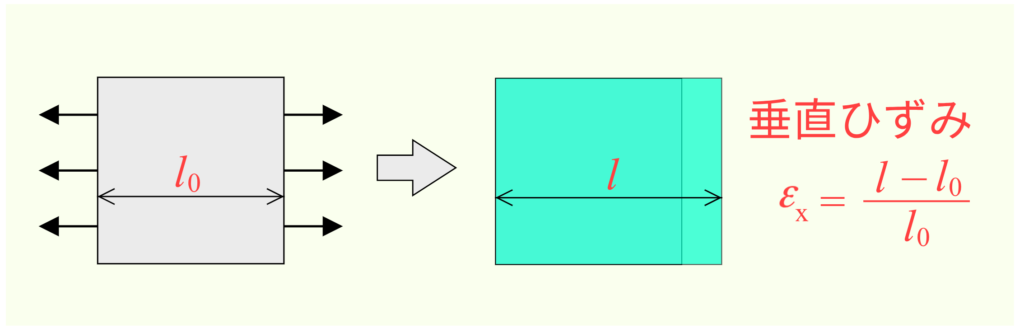
見ての通り、「長さ」を「長さ」で割っているので、出てくる値は無次元、つまり単位なしとなる。当然だが、計算するときには「伸び」と「元の長さ」の単位を揃える必要がある。例えば、伸びが1 mmで、元の長さが1 m（= 1000 mm）のとき、1 ÷ 1 = 1としてしまうと間違いで、正しくは1 ÷ 1000 = 0.001としなければならない。
ただ（%）で表すこともある（ちなみに（%）というのは単位ではない）。ひずみが 0.1というのと、10（%）というのは同じ意味だ。
1（με）= 1×10-6、1（%）= 0.01
1000 mmの棒が1 mm伸びたときのひずみは、0.001 もしくは 0.1 % もしくは 1000 με
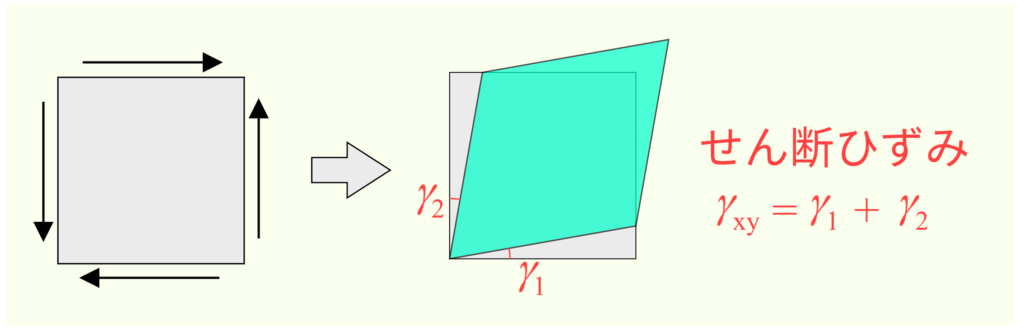
材料の変形は、上で登場したような垂直に伸びたり縮んだりするケースだけではない。面を摩擦するような負荷（せん断応力）を受けるときは、変形は角度のゆがみとして現れる。この角度のゆがみのことをせん断ひずみと言い、垂直ひずみと同じく単位はない。ただ、せん断ひずみは上記の通り、角度のゆがみ量となって現れるので、この角度のゆがみのことを言うときは当然単位はある。この時、単位は（°）ではなく（rad）を使うことに注意しよう。
単位を使いこなすのは超基本
単位を正しく使いこなすというのはとっても重要なことだ。小テストや練習問題でいつも答えが合わない人は、ぜひ単位についてもう一度確認してほしい。
また、公式を使うときにも単位に注意する必要がある。そのあたりの話は以下の記事にまとめている。ただただ単位に気を配るだけでなく、計算ミスを激減させるテクニックについても紹介するのでぜひ読んでみてほしい。
材料力学 公式を正しく使い、計算ミスを減らすコツ【材力 Vol. 0.3】
- 単位をしっかり理解して自由自在に使いこなそう
- モーメント：【N・m】
- 応力：【MPa】=【N/mm2】
- ひずみ：単位なし
