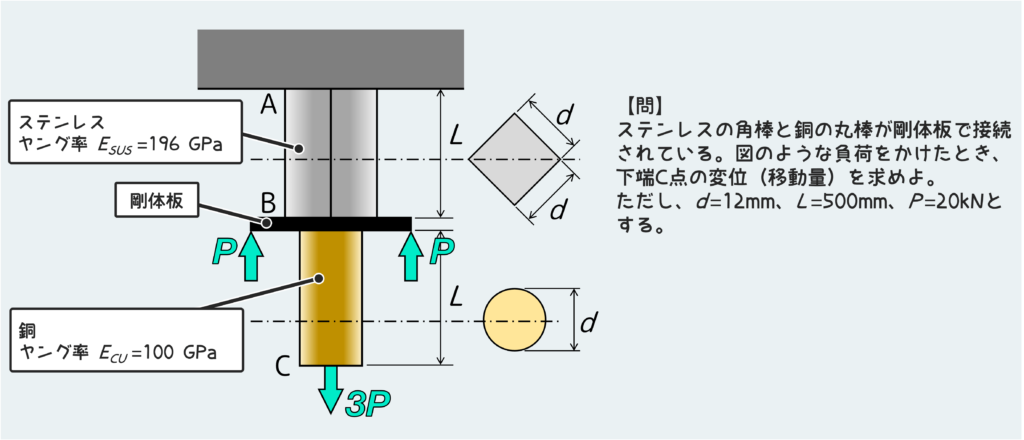
今回は引張圧縮を受ける棒の変形に関する練習問題。
今回の難易度は「 」で、超基礎問題です。
Contents
材力練習問題を解く上でのポイント
今回の問題を解く上でのポイントは以下の通りだ。
- 自由体の考え方を使って、シンプルな形の組合せに分解する
- 単位に注意して、スマートに計算する
ポイントが理解できていないと感じる人は以下の記事を読んでみてほしい。
材料力学 《全員必見・超重要》自由体の考え方の基礎【Vol. 1.1】
材料力学 《全員必見・超重要》自由体の考え方（引張・圧縮を受ける棒）【Vol. 1.2-1】
材料力学 公式を正しく使い、計算ミスを減らすコツ【材力 Vol. 0.3】
この材力練習問題の解き方
どんな問題もそうだが、シンプルな形というか、それぞれの負荷形態における基本形の組合せに問題を置き換えることが大事だ。
複雑そうに見える問題ほどシンプルな状態の組合せに置き換えて、一個ずつ丁寧に解いていく必要がある。
引張圧縮問題におけるシンプルな形は下図のようなものだ。
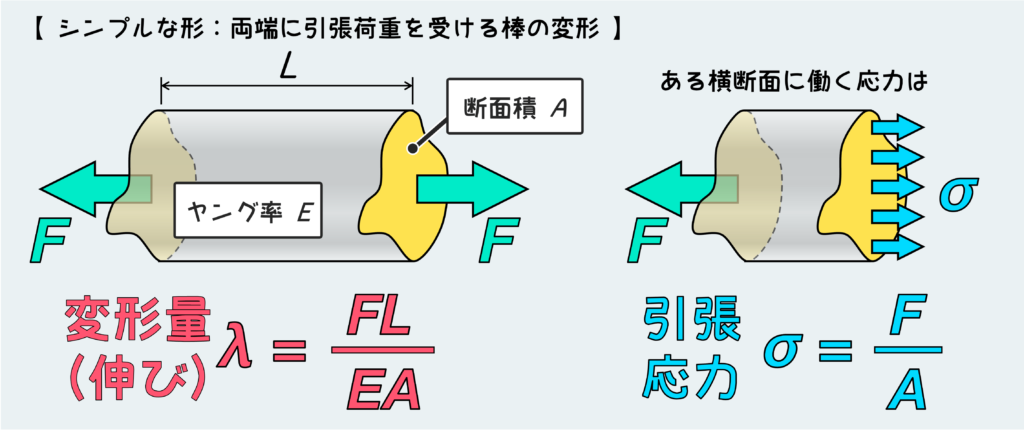
両端に引張荷重を受ける棒の変形とある横断面に働く応力は上のように表せる（今回の問題では応力は使わない）。
ヤング率Eは材質によって決まるもので、断面積や長さは材料の寸法で与えられるものなので、重要なことは荷重Fを正しく見極めることだ。
何度も言っていることだが、『自由体の考え方』を使って内力の伝わり方を把握すれば、この荷重Fを正しく見積もることができる。
では、自由体の考え方を使って、シンプルな形に分解していこう。そして内力を正しく見積もる。
まずは区切りの良いところで分解することを考える。ざっくりした言い方をすると、“何か”が変わっているポイントで切り分ければ良い。
例えば材質だとか、断面形状が変わるような所で切り分ける。材質や断面形状が変わると、上で説明した公式をそのまま使うことができないので、こういう位置では切り分ける必要がある。
今回の問題の場合はB点で形状と材質が変わるので、下図のように切り分けると良い。
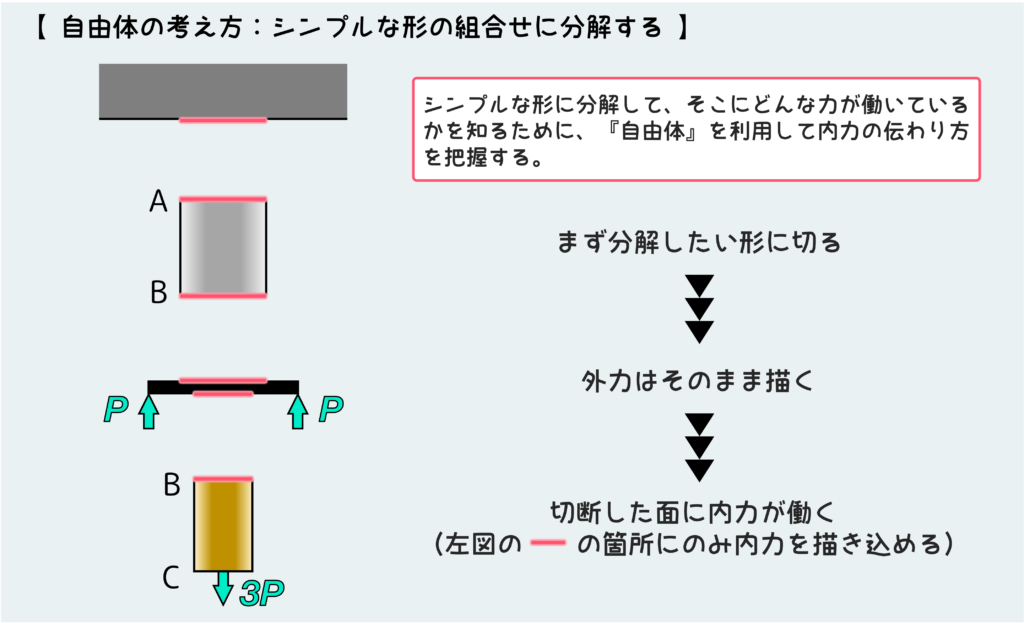
材料を仮想的に切断するポイントを決めたら、まず切る。そして、外力はそのまま描けば良い。
その後内力を描き込んでいくわけだが、内力を描き込めるのは今切断した面だけだ。
切り分けた自由体がつり合いを取れるように、内力を決定していく必要がある。
下図で説明している通り、未知の内力が少ない場所から順番に考えていき、平衡条件と作用・反作用の法則を利用して、内力を決定していく。
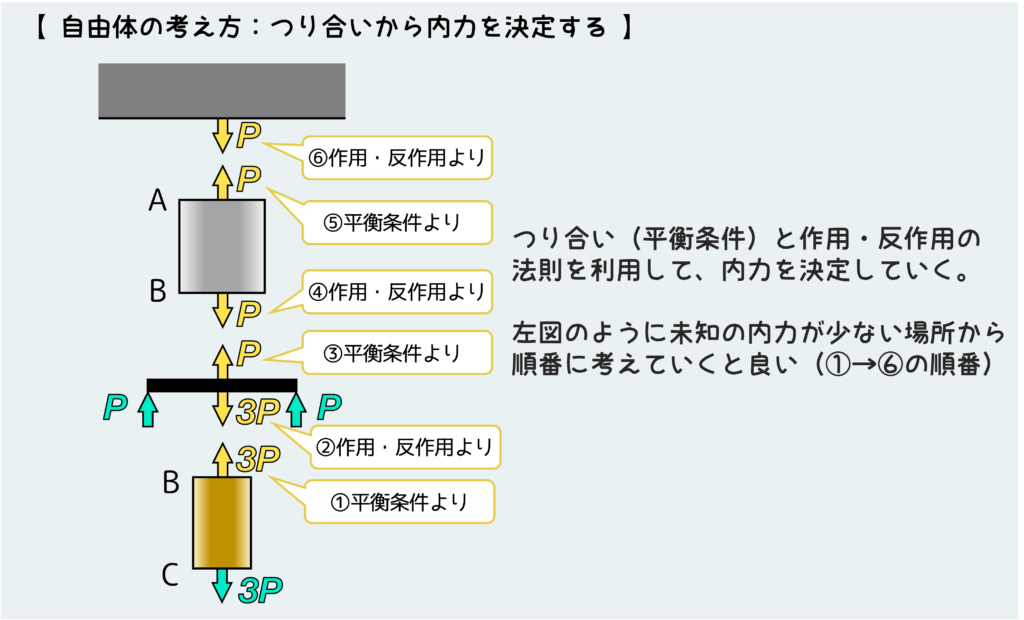
ここまで来ればもう解けたようなものだ。
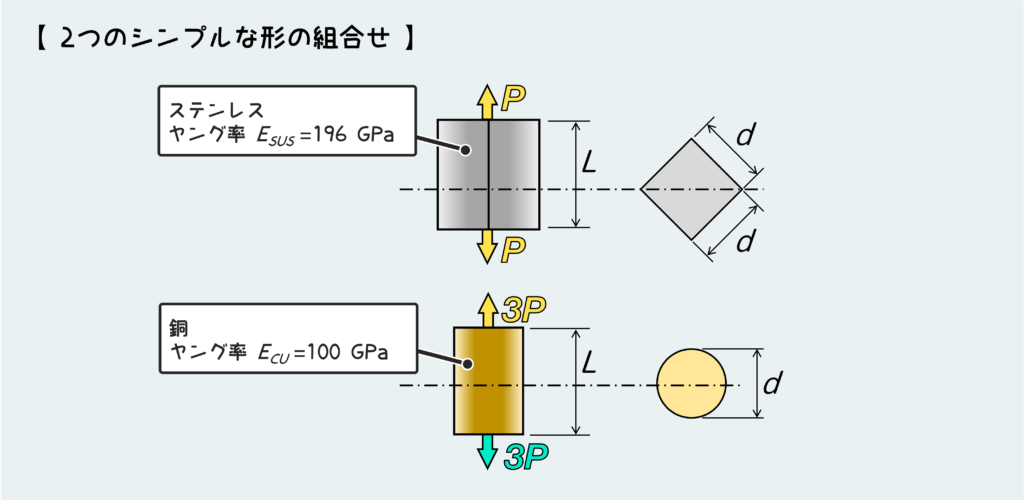
内力を決定できたので、今回の問題は下図のように２つのシンプルな形の組合せに置き換えることができた。
この２つの材料の変形を考えれば、問題の構造全体の変形を知ることができる。
では実際に変形量を計算していく。
ここで注意したいのは『単位』の扱いについてだ。
『単位』を軽く見ている学生は非常に多いのだが、単位が間違っていたら誤った答えに辿りついてしまい、極めて危険だ。
材料力学の計算において、問題文では色々な単位で数値が与えられるかもしれないが、下図のような単位に直してから式に代入するとうまくいくことが多い。
これはなぜかというと、【N/mm2】=【MPa】という関係があるからだ。
これは絶対に知っておくべき関係性なので、しっかり押さえておこう。
ここが分かっていれば、単位について悩むことはなくなるはずだ。
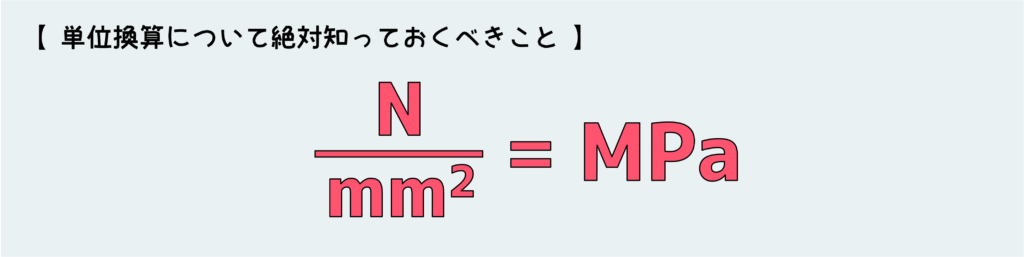
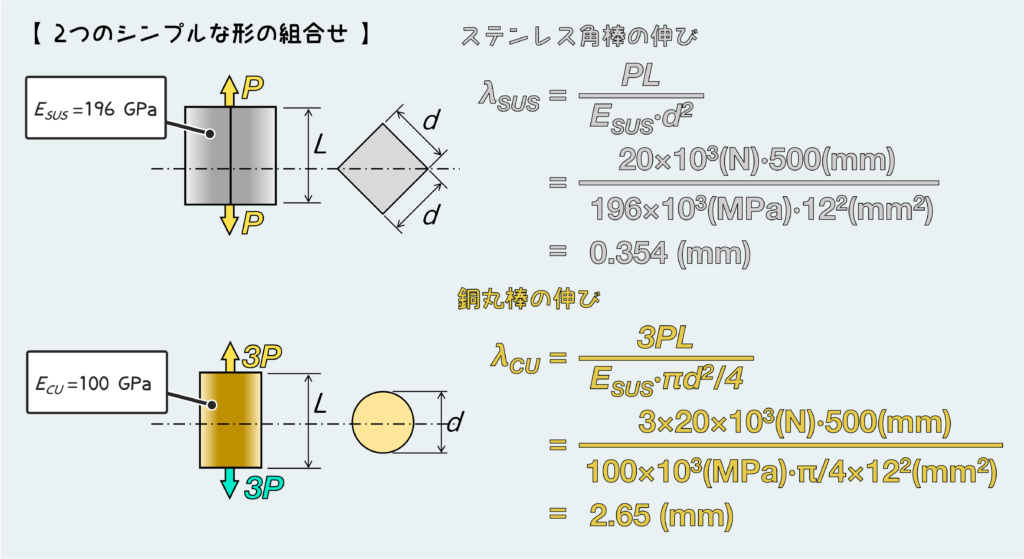
では今回の問題で、それぞれ２つの棒の変形量を求めてみよう。
２つのシンプルな形に分解したことで、公式がそのまま使える。
上で説明した単位換算に注意しながら、公式に数値を代入すると下図のように計算できる。
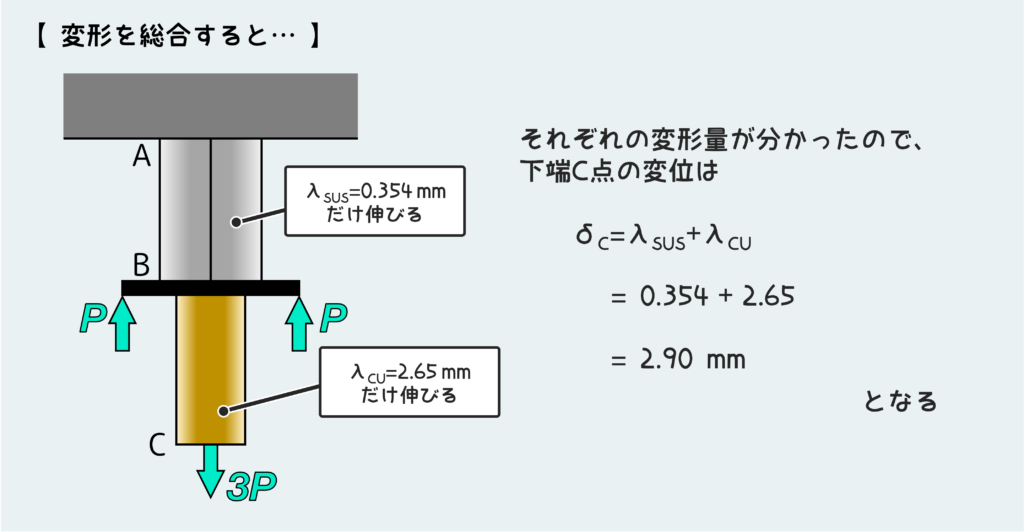
この２つの棒の変形量がわかれば、この構造全体の変形を考えるのは簡単だ。
今回の問題では下端C点の変位（つまり移動量）が問われている。
ABの伸びとBCの伸びを合計した分だけC点が下方向に動く訳だから、先ほど求めた変形量を足し合わせればいいことになる。
類似の材力練習問題
今回と同じく引張圧縮に関する問題を以下にまとめているので、他の問題にもチャレンジしたい人は見てみてほしい。
引張圧縮に関する復習
引張圧縮に関してめちゃくちゃ分かりやすく説明した記事たちはこちら。
改めて基礎を確認したい人は以下の記事を読んでみてほしい。
