材料力学　絶対必須！曲げを受けるはりの変形量を簡単に導けるミオソテスの方法【材力 Vol. 6-8】

今回の記事ではミオソテスの方法について解説したい。

前回の記事では、曲げをうける材料（はり）の変形量（たわみや傾き）を知る手段として曲げの微分方程式について説明した。微分方程式はたわみや傾きを位置xの関数として導くことができるので、変形後の状態の全体像を把握するのに向いている。しかし、式を解くのがやや面倒である。特に、ある特定の点の変形量が知りたいときに微分方程式をわざわざ解くのは効率が悪い。

そこで、ミオソテスの方法である。ミオソテスの方法は、ある特定のパターンを基本形として変形量を公式化しておき、どんな問題もこの基本パターンの組合せとして考えることで楽に解くことができるという方法だ。

この記事ではミオソテスの方法の基本的な使い方を説明したい。使い方は分かってるから、具体例で理解を深めたいという人は次の記事を読んでみてほしい。（まだ執筆中です、すみません）

曲げの微分方程式について知りたい人は、この次の記事もぜひ読んでみてほしい。

材料力学　大切なことはたった１つ！曲げの微分方程式の考え方【材力Vol. 6-7】

ミオソテスの方法とは・・

「片持ちばりの先端のたわみと傾き」を公式化して利用

ミオソテスの方法とは、はりの曲げ問題において簡単に変形量（たわみや傾き）を求めるために使われる方法だ。基本的な問題の変形量（たわみと傾き）を公式として持っておき、それを利用してその他の複雑な問題の変形量を求める。

公式として利用するミオソテスの基本パターンは、外力の種類によって３つある。

いずれも『片持ちばり』の形だ。ここで公式化して使うのは、片持ちばりの先端のたわみδと傾きθだ。以下に紹介する３つのパターン（モーメント・集中荷重・分布荷重）のように、片持ちばりの先端のたわみと傾きを公式化しておき、どんな問題もこれの組合せとして考える訳だ。

公式自体は難しくなく、楽に覚えられるはずだ。なので、ミオソテスの方法を使う上で肝になってくることは、いかに片持ちばりのカタチ（解けるカタチ）に持っていくか、ということだ。

パズルを解くような頭の柔軟さが必要だが、コツを掴めばこれもそんなに難しくない。次の記事（まだ執筆中です、すみません）で説明する具体例を通して、ミオソテスの使い方をしっかり理解してほしい。

ミオソテスの基本パターン

モーメントを受ける片持ちばり

まず、先端にモーメントMが作用する片持ちばりの場合だ。このとき、先端のたわみと傾きは下のように表せる。

集中荷重を受ける片持ちばり

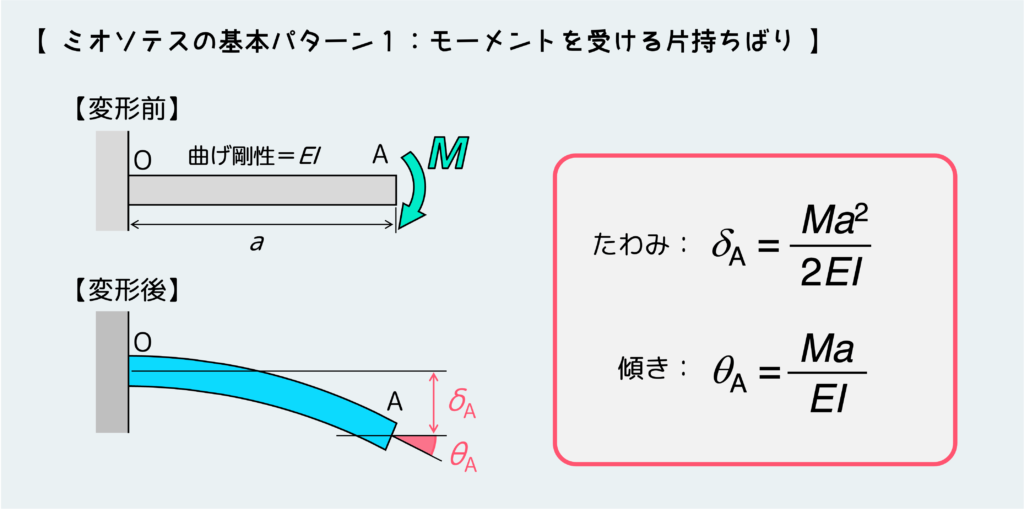
次に、先端に集中荷重Pが作用するときだ。先端のたわみと傾きは下の絵の通り。

分布荷重を受ける片持ちばり

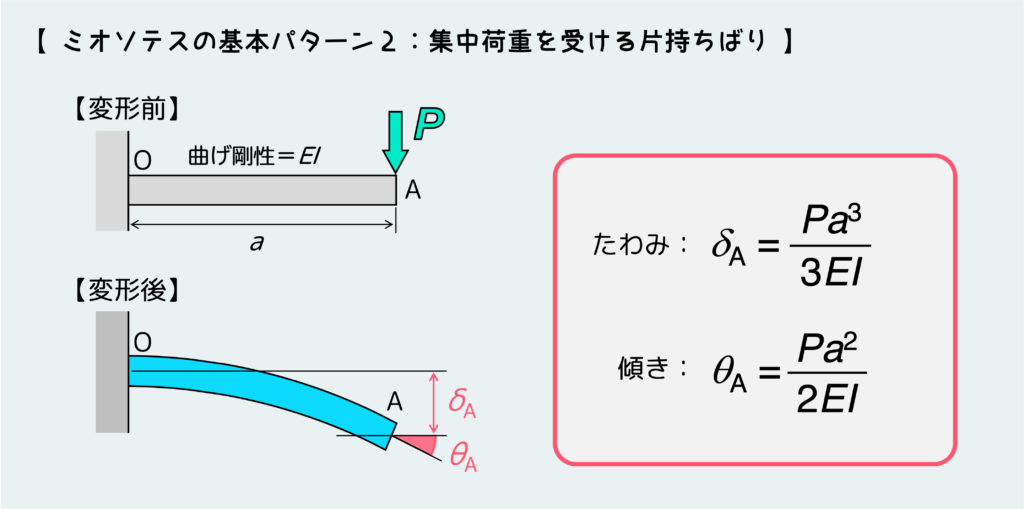
最後に、分布荷重がはり全体に作用する場合だ。

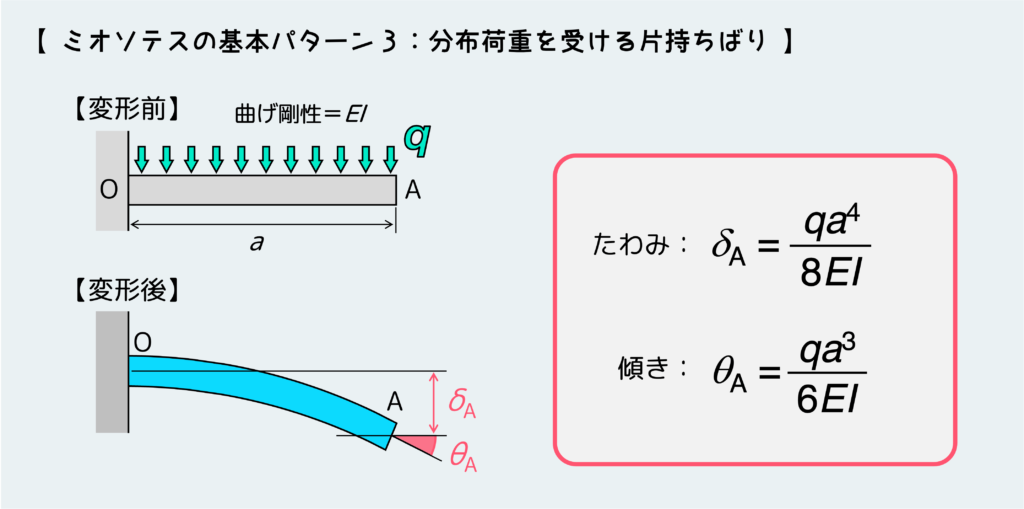
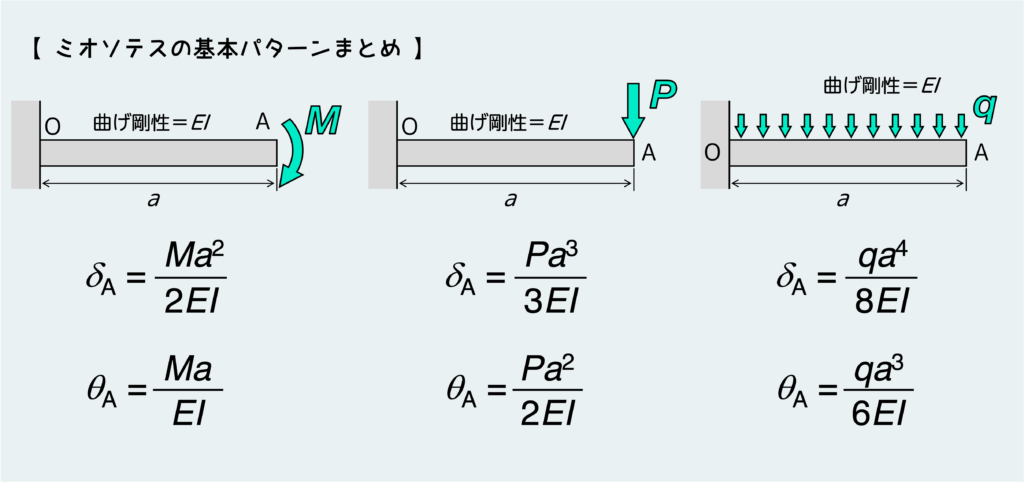
まとめると上の絵のようになる。

どのケースでも変形量は、分母に“EI”がきており、分子は“外力×（はりの長さ）の累乗”となる形で表せる。さらに、外力の種類がモーメント→集中荷重→分布荷重となるに伴い、（はりの長さ）の次数が１つずつ増えていることが分かるだろう。モーメントは（力）×（長さ）だし、二次元問題における分布荷重は（力）÷（長さ）なので、このような次数の変化は当然だ。

つまり、この公式を覚えようと思ったら、基本の形だけ頭に入れてあとは分母の８とか６とか３とかさえ覚えれば良いってことだ。

ミオソテスの使い方

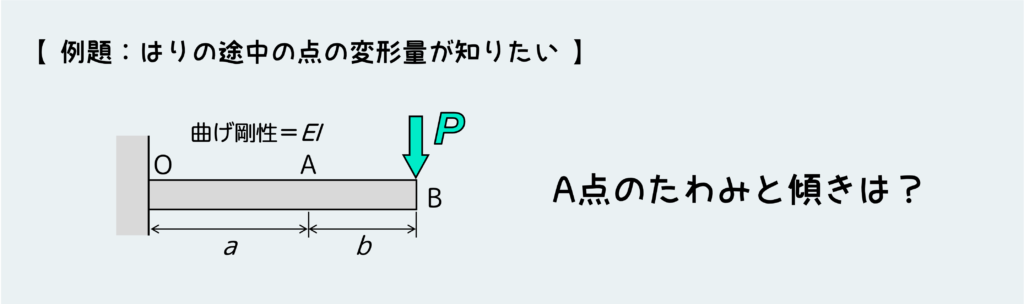
では、特定の３パターン（片持ちばりの形）が分かったところで、具体的な使い方を解説していこう。以下では最も簡単な例として「はりの途中の点の変形量が知りたい」場合を解説していこう。

その他のもっと発展的な具体例については、次の記事（まだ執筆中です、すみません）を見てもらいたい。

はりの途中の点の変形量が知りたい

下の絵のような問題を考えてみよう。片持ちばりの先端に荷重Pが作用している訳だが、今知りたいのは先端B点ではなく、はりの途中のA点の変形量だとする。こんなときは、どうすればいいだろうか。

繰り返しになるが、ミオソテスで利用する基本パターンは『片持ちばりの先端の変形量』なので、問題をいかにこの形に変換していくかが重要だ。

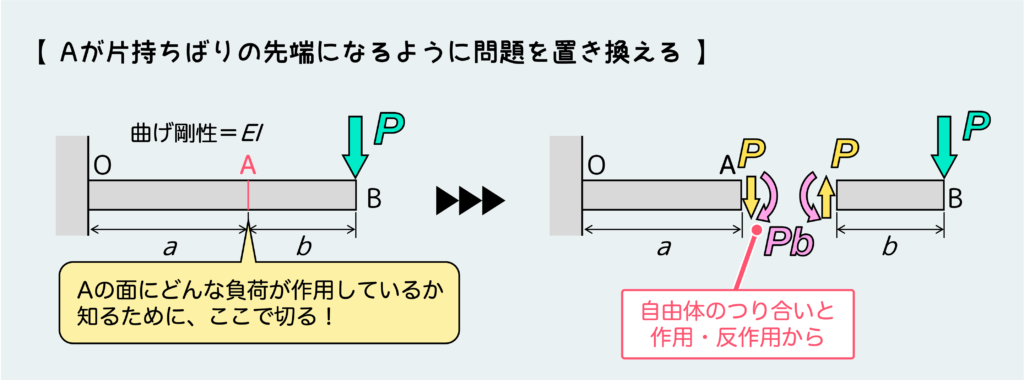
今回の場合は、はりの途中のA点の変形量が知りたいので、このA点が先端になるように問題を置き換えれば良い。つまり、与えられた問題「先端に荷重Pが作用する片持ちばりOB」を「先端に何かの力が作用する片持ちばりOA」という問題に置き換えてしまう訳だ。

ここで重要なのは『はりOAがどんな負荷を受けているか』ということだが、これを明らかにするためにはもちろんAで切断してAの断面にどんな負荷が伝わっているかを考えなくてはならない。つまり、下図のようにAで切った自由体のつり合いから、内力の伝わり方を把握する必要がある。

上のようにAで切って内力の伝わり方を考えると、最初の問題（はりOB）のOA部分に関しては、『先端に荷重Pと曲げモーメントPbが作用する片持ちばりOA』と置き換えて考えられることが分かる。

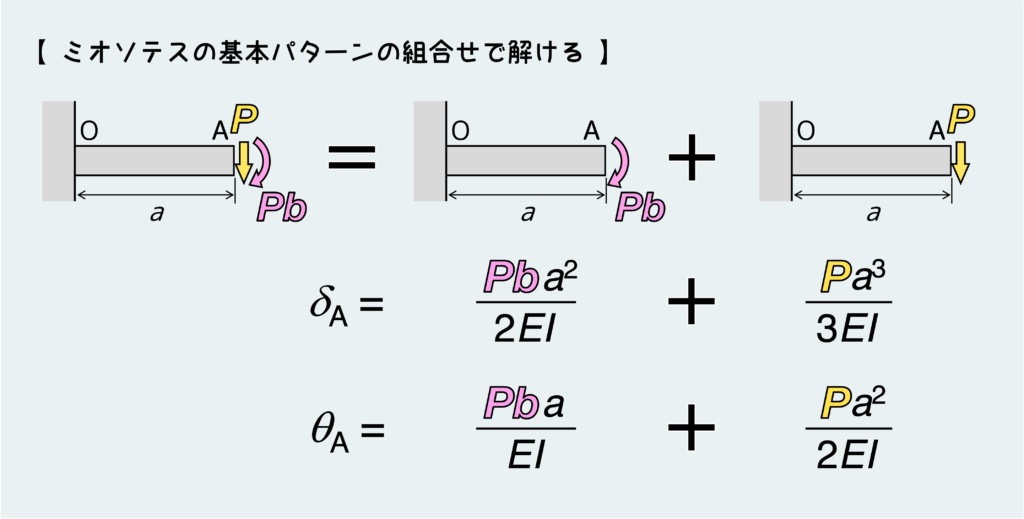
ここまで来ればあとはミオソテスの基本パターンの組合せだ。

つまり、上で紹介した基本パターン１のモーメントのところに“Pb”を入れて、基本パターン２の荷重のところに“P”を入れてそれらを足し合わせれば（重ね合わせ）、A点の変形量が求まる。

以上で、先端に負荷を受けるはりの途中の点の変形量が求められた。

この例で見てきたように、いかに片持ちばりの形に持っていけるかが大事なことだ。その上でポイントは２つある。１つ目は、片持ちばりの形に置き換えたときにその置き換えたはりがどんな負荷を受けた状態になっているかを見極めること。そして２つ目は、重ね合わせの原理が使えること。

まとめ

今回の記事では、はりの曲げにおける変形量を扱う問題で必須なミオソテスの方法について解説してきた。基本的な使い方は上で説明した通りだが、もちろん問題が複雑になると、今回説明した例題のように単純ではない。

そうは言ってもいくつかのパターンを理解すれば、ほとんどどんな問題も解けるようになると思う。

次の記事（まだ執筆中です、すみません）では、もう少し発展的な具体例をいくつか紹介したいので、ぜひ次の記事も合わせて読んでみてほしい。