曲げによって発生する応力、そして変形を考えるためには『断面二次モーメント』っていうものを理解しないといけない。
少し複雑に感じるかもしれないが、これはしっかり意味を理解しておこう。
いろんな断面形状に関する断面二次モーメントが一覧にまとめてあったりするが、意味を理解していないとちゃんと使いこなすことはできないだろう。場合によっては間違った結論を導き出してしまうかもしれない。
という訳で、この記事では断面二次モーメントの意味について解説していきたい。
- 断面二次モーメントとは、断面の形状的な曲がりにくさを表すパラメータ
- 引張・圧縮問題で言うところの『断面積』みたいなもの
- 断面二次モーメントが大きいと曲がりにくい、小さいと曲がりやすい
- 曲げの中心軸(z軸)から離れた場所に多くの断面が存在するほど、断面二次モーメントは大きくなる
- 断面二次モーメントは応力や変形量(たわみや傾き)を計算するときに使う
夢へ駆ける少女の姿に感涙!!
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか?」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい!」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanならなんと3巻まで無料で読めてしまいます!まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです!
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!
断面二次モーメントとは・・
ずばり断面二次モーメントとは、部材の寸法・形状によって決まる量で、その部材の曲がりにくさを表すパラメータである。
材料の変形のしにくさ(剛性と言ったりする)は、『材質』と『形状・寸法』の2つの影響を受けて決まる。
材質についてはすぐに理解できると思う。同じ形状のゴムと金属の棒があったとしたら当然ゴムの方が変形しやすく、金属は同じ負荷をかけても全然変形しないだろう。このような、材質によって変わる変形しにくさを受け持つパラメータがヤング率のE や横弾性係数のG という訳だ。
一方、材質が同じでも形状が変わると変形量も変わる。大雑把に言って、大きな断面を持つ材料の方が変形しにくい。
断面二次モーメントとは、このような断面の形状・寸法によって変わる変形しにくさを表すパラメータの1つで、材料を曲げる場合に使われる。
引張・圧縮問題との比較
では、より断面二次モーメントについて理解・実感していくために引張・圧縮の場合と比較してみよう。
引張・圧縮のときには、断面二次モーメントなんていう難しいモノは登場しなかった。が、引張圧縮の場合ももちろん断面形状によって変形のしにくさは変わる。引張圧縮の場合に、このような断面形状による変形のしにくさを表すパラメータとして使っていたのは何だったかと言うと、それは『断面積』だ。
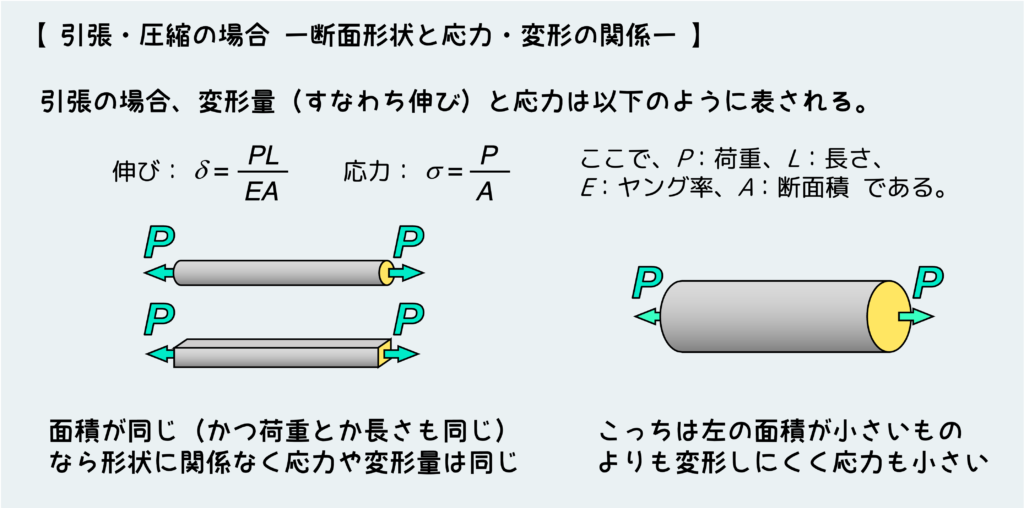
引張・圧縮の場合の応力の式、変形(伸び・縮み)の式を思い出すと分かるように、断面積が大きくなるほど発生する応力は小さくなり、変形量も小さくなる。逆に断面積が小さいと、応力も変形量も大きくなる。
引張・圧縮の場合はとってもシンプルで、感覚的にもすごく理解しやすかったと思う。
じゃあなぜ曲げの場合は『断面積』ではなく、『断面二次モーメント』を使わないといけないのか?
下のような例を見てみよう。
誰でも下敷きを曲げたことぐらいあるだろう。下の例では、横長に持った下敷きを曲げる場合と縦長に持った下敷きを曲げる場合を比較している。誰でも簡単にイメージできると思うが、この2パターンではびっくりするほど曲がりにくさは違う。同じ断面積なのに、だ。縦長に持った右側の例の方が、当然曲がりにくい。
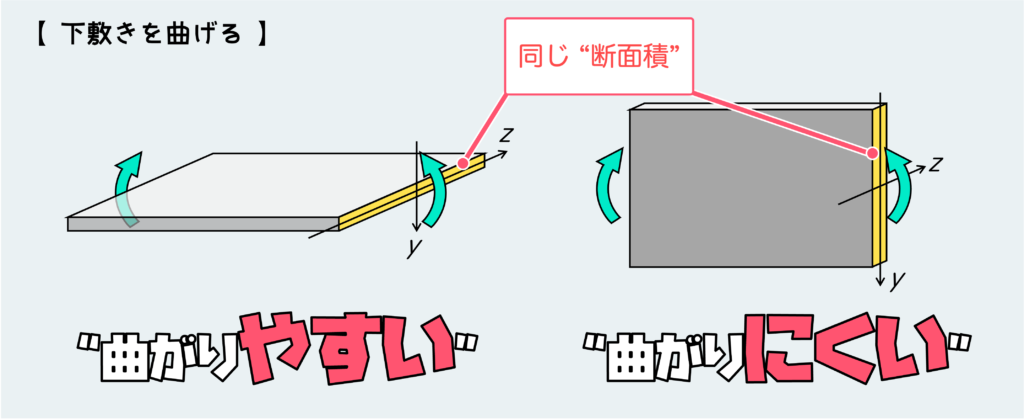
つまり、曲がりにくさは断面積だけでは決定できず、形状の影響を強く受ける。正確には、曲げの中心軸(図のz軸)に対する断面形状と寸法によって決まる。なので、引張・圧縮の場合とは違い、断面積だけで曲がりにくさを表現できないので、断面二次モーメントを使う必要がある。
まとめると、曲げの中心軸(上の図でのz軸)を基準として見た断面形状・寸法によって決まる曲がりにくさを表すパラメータが断面二次モーメントという訳だ。
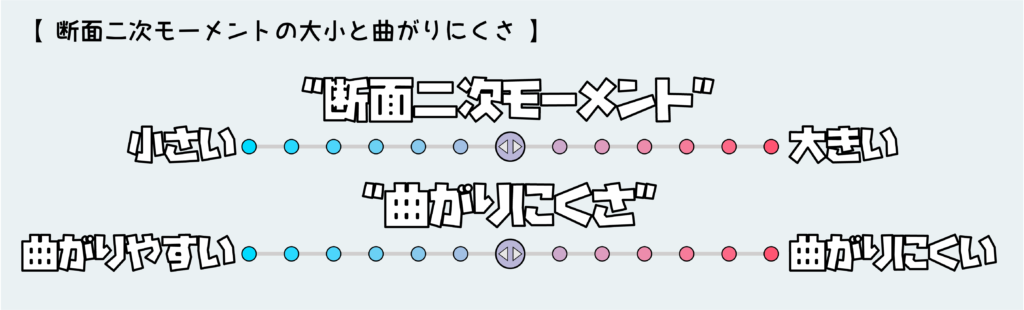
では断面二次モーメントのことがおおよそ理解できたところで、断面二次モーメントの大小と曲がりにくさについて整理しておこう。
断面二次モーメントが大きくなる場合、同じ負荷(曲げモーメント)が作用しても曲がりにくくなる。曲げによる変形量が小さくなるということだ。また、発生する曲げ応力も(多くの場合)小さくなる。なので、(寸法・重量やコストの制限がなければ)安全側にシフトすることになり、良いことだ。
反対に断面二次モーメントが小さくなる場合、曲がりやすくなることを表しており、変形量は大きくなるし、曲げ応力も(多くの場合)大きくなる。なので、破壊のリスクが高まることになる。
断面形状と断面二次モーメントの関係
じゃあどんな断面形状にすれば断面二次モーメントを大きくすることができるだろうか?
まず下の絵を見てほしい。図のような向きに曲げるとき、設定した座標系と断面二次モーメントの定義に注目してほしい。
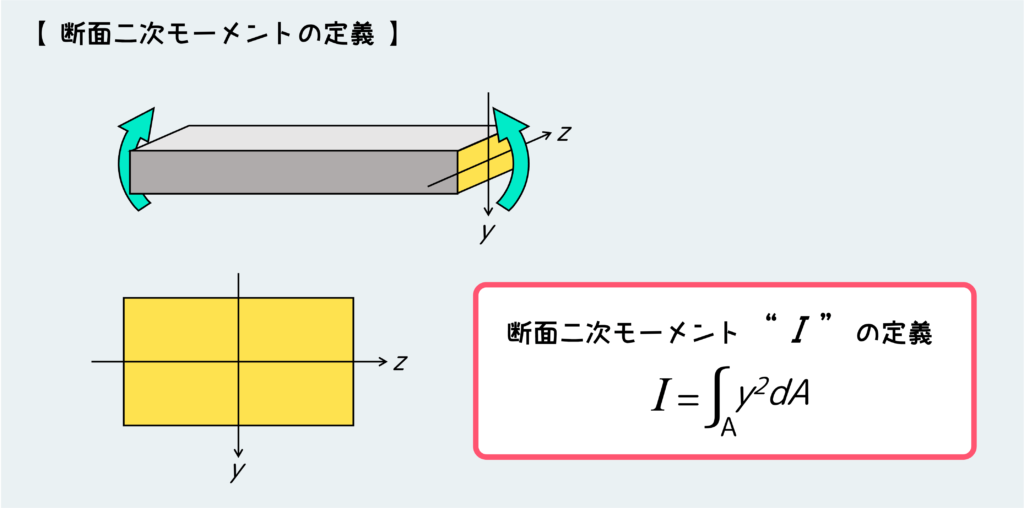
これの意味は、断面上のすべての位置について “y2” を足し合わせていく(全断面に対して積分する)ということなんだけど、まあこの積分の意味は分からなくてもいい。ここで言いたいのは、上図のような向きで曲げるような絵を描いたとき、断面二次モーメントとは『曲げの中心軸であるz軸からy方向にどれだけ離れたところに断面が存在するか』を表しているということ。
つまり、縦方向の曲げに対して、横方向(z方向)への断面の拡がりはあんまり断面二次モーメントには効かなくて、縦方向(y方向)へ拡がった形になる方が断面二次モーメントを大きくする効果が極めて大きいってことだ。
だから下敷きの例のように、横長に配置した場合よりも縦長に配置した場合の方が、断面二次モーメントは極めて大きくなり、曲がりにくくなるってことだ。
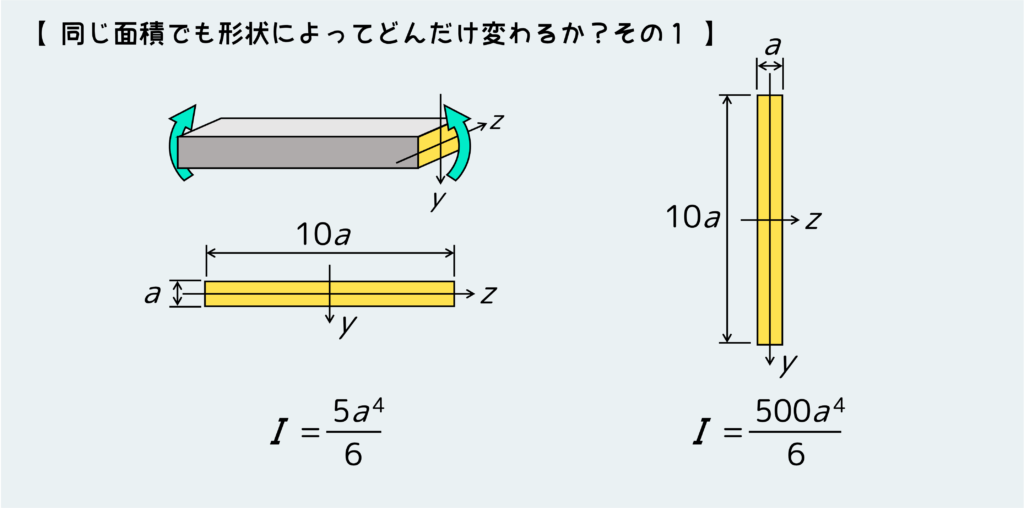
このように、縦方向に曲げる(この言い方はあまり良くない気もするが)ときには、縦方向の寸法が断面二次モーメントに強く影響するので、縦長な形状になるほど断面二次モーメントが大きくなると考えて良い。
また、全体的な縦長・横長の比率は変わらなくても、相対的にz軸から離れた場所に多くの面積がある方が断面二次モーメントは大きくなる。下の例を見て、このことも理解しておこう。
(下の図の場合ももちろんz軸を中心にy軸方向に曲げることを想定している。)
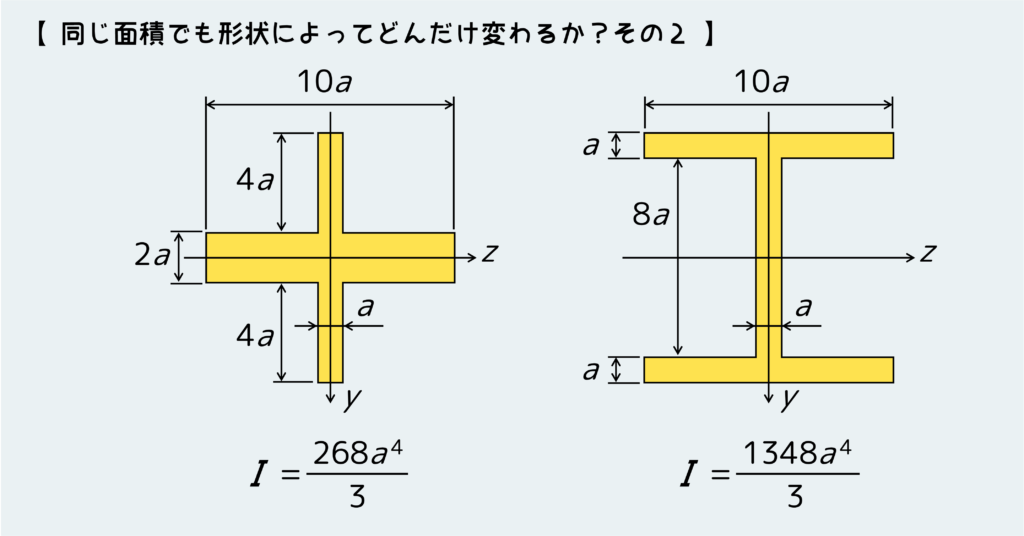
どう使う? ー 曲げ応力や変形量の計算に使う
引張・圧縮の場合の『断面積』がそうであるように、断面二次モーメントは曲げの応力や変形量を計算するために使う。
ある曲げモーメントが働く棒に発生する応力と変形は下のような形で表せる。引張・圧縮の場合との類似性にも気が付いてほしいので、引張・圧縮の場合の式も合わせて載せている。
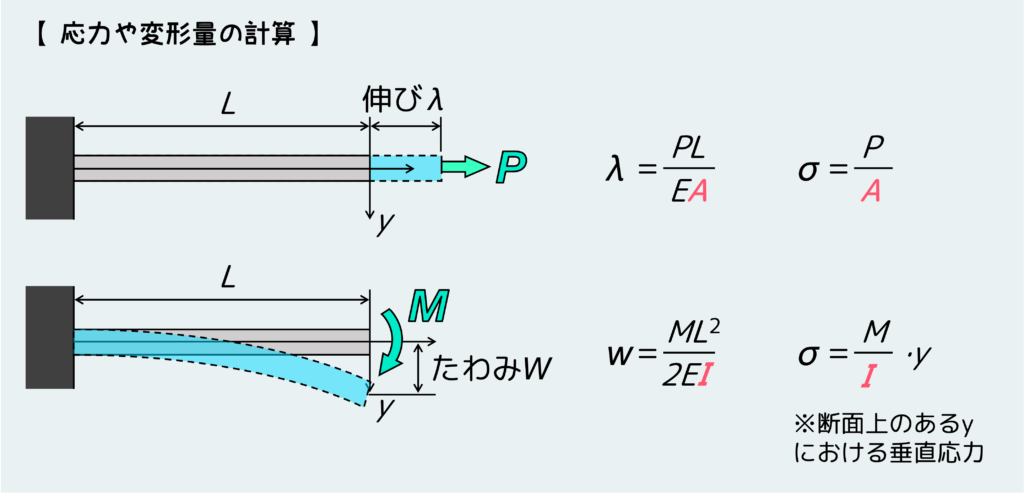
まず難しいことを考えずに式だけ見ると、非常に引張・圧縮問題のときと似たような形になっていることが分かると思う。引張・圧縮問題における『断面積』が持つ役割と同じように、断面二次モーメントが大きいほど応力も変形も小さくなるような式の形になっている(まあこれは最初に説明した通り)。
まとめ
断面二次モーメントって言葉も聞きなれないし、いまいちどういう意味を持ってるのか分かりにくいことと思う。でもそんなに怖がる必要はない。
まあ要するに、形状的な曲がりにくさを表しているパラメータってことだ。引張・圧縮における断面積みたいなものっていう風に捉えてもらえば、とても理解しやすいのではないだろうか。
この記事では断面二次モーメントの具体的な使い方については深く触れていないが、これ以上は曲げの応力分布についてさらに詳しく見ていかないといけないから、この記事ではここまでにしておこう。
次の記事で、曲げ応力について詳しく解説したいと思うので、断面二次モーメントの持つ意味について分かった上で次の記事もぜひ読んでみてほしい。
 曲げモーメントから曲げ応力を計算する方法が絶対分かる記事【材力Vol. 6-6】
曲げモーメントから曲げ応力を計算する方法が絶対分かる記事【材力Vol. 6-6】
- 断面二次モーメントとは、断面の形状的な曲がりにくさを表すパラメータ
- 引張・圧縮問題で言うところの『断面積』みたいなもの
- 断面二次モーメントが大きいと曲がりにくい、小さいと曲がりやすい
- 曲げの中心軸(z軸)から離れた場所に多くの断面が存在するほど、断面二次モーメントは大きくなる
- 断面二次モーメントは応力や変形量(たわみや傾き)を計算するときに使う
研究者を志す者 必読!!
全8巻完結
こんなにも知的探究心を刺激される漫画があったとは!
真理のために命をかけた先人たちの物語。
この作品は、現役研究者である私・ぽるこが衝撃を受けた作品として、特に研究者およびこれを志す者には強く本気でオススメします。今ある常識を疑う心、誰に何を言われようと真理を追求する姿勢に触れ、心が動くこと間違いありません。
私自身、世界のトップ研究者だった師匠によく言われた言葉を思い出します。“目の前の現象に楽な答えを持ち出し、疑うことをやめ、真理の追求という困難な道から逃げていないか!?”
本作はこういった研究者の気概なるものを感じる、必読の価値ある一冊です。全8巻ですでに完結していますし比較的手軽に一気読みできます。気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!






こんにちは。
断面二次モーメントについて分かりやすくまとめられていて、勉強になりました。
ありがとうございます!
1つ質問なのですが、【同じ面積でも形状によってどんだけ変わるか その2】のI=1348a^4/6が348a^4/3になってしまいます…。
お忙しい所、大変恐縮ですが計算式をご教授いただけないでしょうか。
よろしくお願い致します。
連投ですみません…。
誤字がありましたので訂正です。
誤:
I=1348a^4/6が348a^4/3になってしまいます…。
正:
I=1348a^4/6が1348a^4/3になってしまいます…。
小田様
コメントありがとうございます。
小田様のおっしゃる通り、私のケアレスミスで、I=1348a^4/3が正しいです。
申し訳ありません。当該図は修正しております。
また、お返事が遅くなってしまい、大変申し訳ありません。
至らぬ点がございますが、引き続き当サイトをご利用いただけますと幸いです。
今後ともご質問等お待ちしております。
(管理人)ぽるこ