材料力学　フックの法則が使える時と使えない時の違いちゃんと分かってる？【Vol. 2-3】

これまでの記事で『応力』と『ひずみ』についてそれぞれ解説してきた。今回の記事では、この２つの間にある関係性について詳しく説明していきたい。その過程で、最も定番な材料試験である『丸棒の引張試験』についても簡単に触れたいと思う。

「応力」について詳しく知りたい人はこちらの記事を読んでほしい↓

材料力学　応力とは？10分で完全に理解できる 基本かつ超重要な解説【材力 Vol. 2-1】

「ひずみ」について知りたいよって人はこちらの記事をぜひ↓

材料力学　ひずみとは何かめちゃくちゃ分かる解説【材力 Vol. 2-2】

フックの法則は決して万能ではないよ！

この記事で出てくるキーワードはまあみなさんの予想通り『フックの法則』な訳だけど、本当に言いたいことはそうじゃない。

むしろ、“応力とひずみの関係＝フックの法則” という風に盲目的に考えてはダメだ、ということを伝えたい。この記事の結論はずばり、フックの法則はあくまで材料の変形挙動の一側面にすぎず、応力にしてもひずみにしても元々の定義をより大切にすべき、ということだ。

よく言ってるんだけど、何事も公式や定理を形だけ覚えて「はい、コレとアレの関係式はこうでしょ」ってポンと言えたとしても、それは少し危ういんだよね。その式が持っている意味や境界条件（どういう範囲でこの式が適用できるか）とかを理解して使えることが重要だ。

では、ここで出てくる定理『フックの法則』の背景にあるものを考えていこう。一番簡単な例として、丸棒を引っ張っていく場合を例にして、負荷（応力）と変形（ひずみ）の関係について考えてみよう。

丸棒を引っ張っていくときの応力とひずみの関係

まずイメージしてみよう。ある棒にどんどん引張負荷（応力）をかけていくと、材料はどんどん伸びて（ひずんで）いくことが想像できるだろう。当たり前なことに感じるかもしれないけど、こういうイメージはとっても大切だ。このイメージをちゃんと数学的に取り扱えるように数式化していきたいんだけど、この情報だけだと、まだ応力とひずみの関係式を得るにはほど遠い（ある変数の増加に応じてもう一方も増加するような関数は山ほどある）。

もっと意味のある情報を得るためにはどうするか？頭の中だけで考えるのは限界がある。それなら実際に棒を引っ張りながら、負荷の大きさと変形量を計測してみれば良い（実験）。機械系の学生であれば大学２年や３年のときに材料実験の講義があるはずだが、ここでは材料の引張試験の概要を簡単に説明しながら、応力とひずみの関係について解説していこう。

丸棒の引張試験 ー 弾性、降伏そして塑性 ー

引張試験の概要を簡単に絵にすると下図のようになる。うまいこと応力とひずみを計測できるような形状にした金属材（試験片と呼ぶ）の両端を引張試験機でつかむ。試験機には試験片に働いている荷重の大きさを測定するセンサーが付いている。また、変形量は試験片中央部に伸び計という計測器を取り付けて測定する。

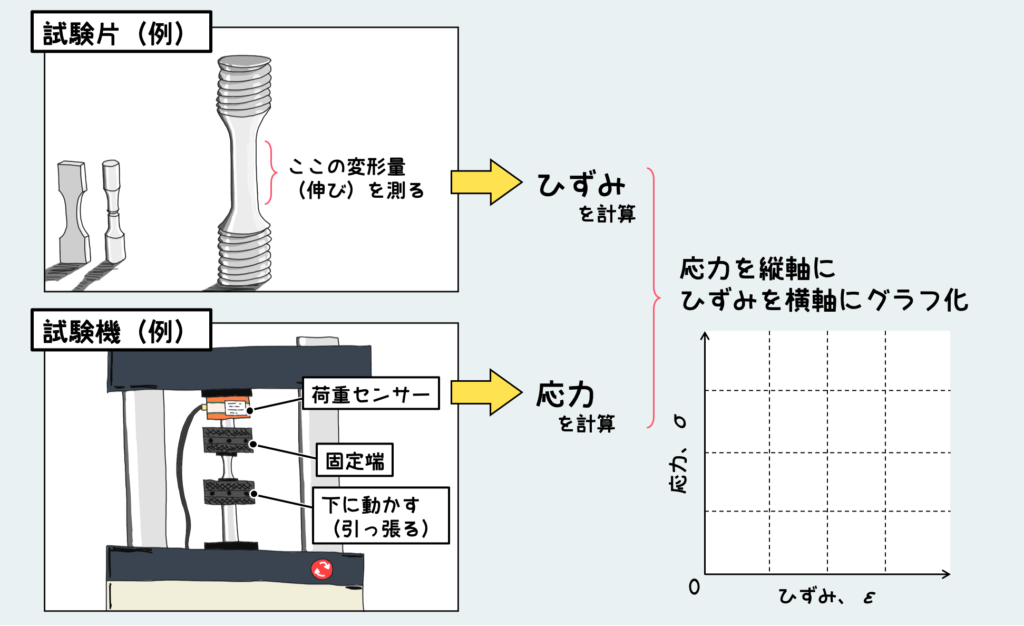
試験片をつかんだ部分の上下どちらかはガッチリ固定されており動かないようになっている。もう一方を少しずつ動かしていき、その時の荷重と変形量を随時測定していく訳だ。荷重から応力を、変形量からひずみを計算し、それらをグラフ上にプロットしていくと、『応力ーひずみ線図』というものが得られる。これが材料の最も基本的な強度特性を表すものであり、色々な設計の元となっている。

序盤は負荷と変形が比例関係

さて概要は以上の通りだ。実際に試験を開始すると、どんな風なデータが得られるか説明しよう。

試験片のつかんでいる部分を少しずつ動かして（引っ張って）、時事刻々変化していく応力とひずみを測定する。例えば、ひずみが 0 → 2 → 4 → 6 → 8 と増えていくとき、応力はどうなるかと言うと 0 → 10 → 20 → 30 → 40 というような感じで計測できるだろう（イメージの話なので数値は適当だし、あえて単位は付けてません）。これが意味するのはつまり、応力とひずみは単純な比例関係にあるということだ（あーよかった応力とひずみの関係は結果的に最も単純な関係式で表せる）。

これを関係式として表すと「σ = Eε 」の形となる。これが、応力とひずみが比例関係にあることを表している『フックの法則』だ。教科書の最初の方で登場するフックの法則とは、このような材料の変形序盤の応力ーひずみ関係のことを言っている訳だ。

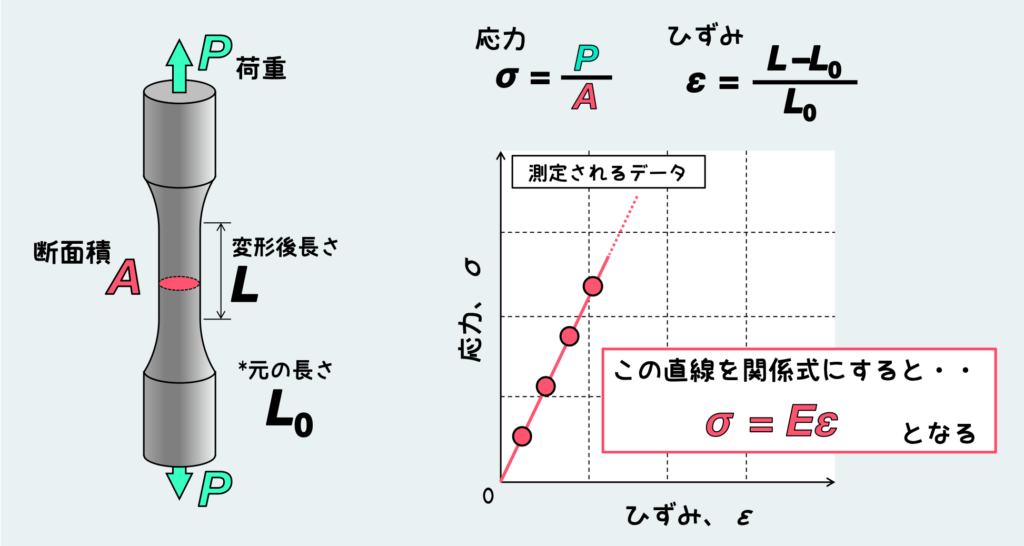
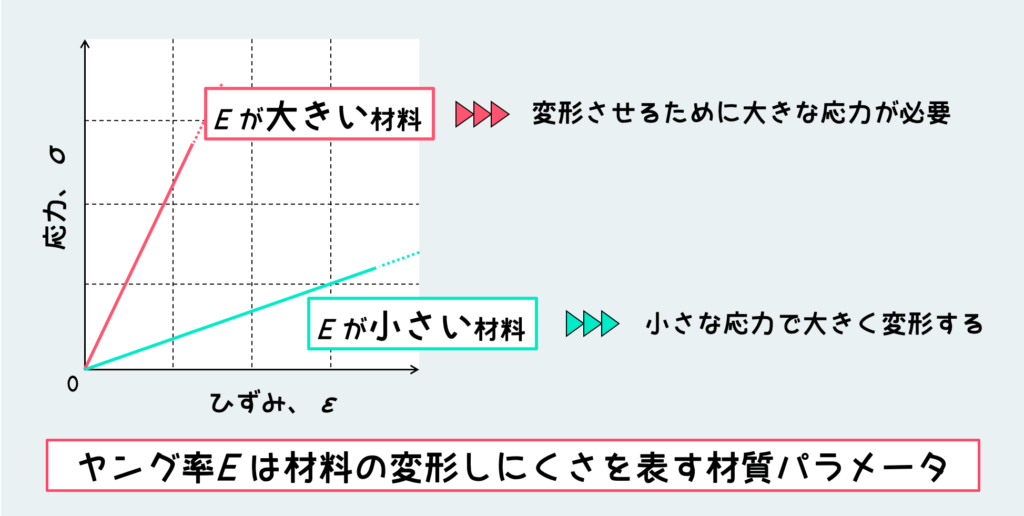
さて、フックの法則は単純な比例関係というだけあって式の形は超簡単だ。この式が意味しているのは、応力とひずみが比例関係にあるってことはもちろんなんだけど、両者を結びつけている”E ”の役割にもぜひ注目してほしい。ここで “E ” は比例定数であり、ヤング率もしくは縦弾性係数と呼ばれるものだ。

比例関係における比例定数ってのはグラフの傾きを表している。つまりヤング率E が大きいと、応力とひずみの関係をプロットした直線はより急勾配になり、変形させるために大きな負荷が必要であることを意味する。逆にE が小さいと、グラフ上の直線はより寝た形になり、少しの負荷で大きく変形することを示している。ゴムみたいな材料だとE はとても小さく、金属みたいな材料だとゴムなんかと比べてE はめちゃくちゃデカくなる。このように、E は材質によって決まる材質パラメータであり、材料の形状や寸法とは無関係に材料の変形のしにくさを表している。E のような変形のしにくさを表す材質パラメータを材料の『剛性』と呼んだりもする。

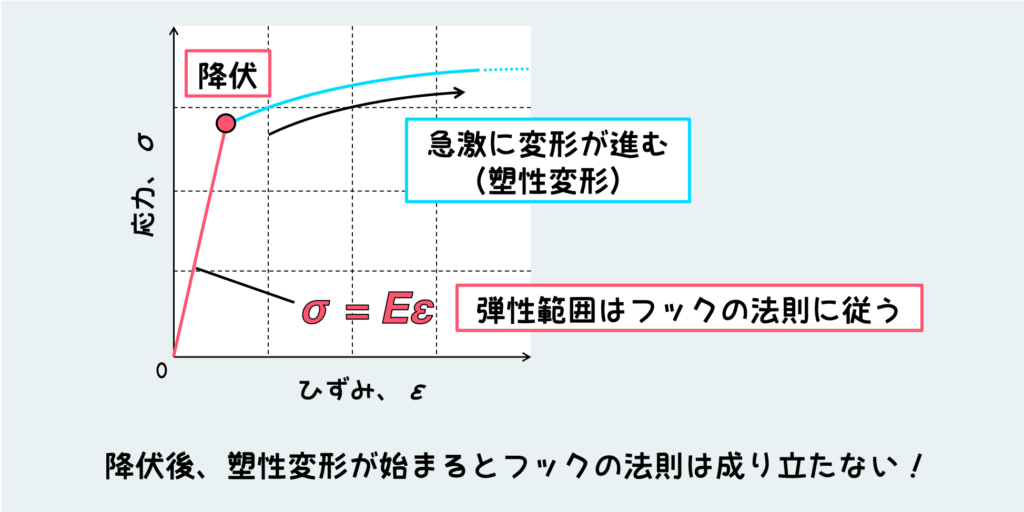
降伏と塑性変形 ー フックの法則の破綻

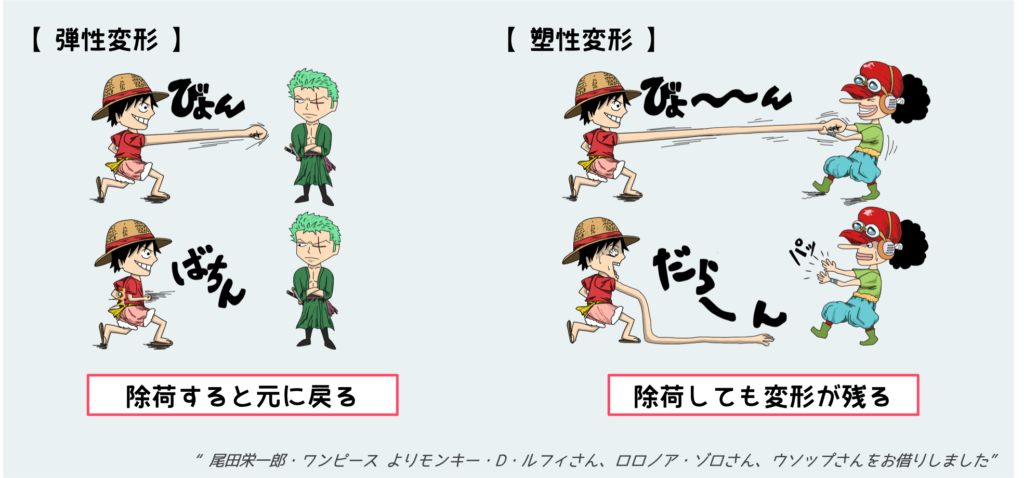
上記のようにフックの法則に支配されているような領域では、変形量（ひずみ）は比較的小さく、かけている負荷を取り除くと変形前の状態まできれいに戻る。こういう除荷するとなくなってしまうような比較的小さい変形を「弾性変形」という。

しかし、さらにどんどん引っ張っていきある地点を超えると、急激に変形が進み、大きく変形するようになる。この領域になると、もはや負荷を取り除いても変形前の状態には戻らず、大きな変形が残ったままになる。このように除荷しても残ってしまう変形を「塑性変形（永久変形）」と言い、この塑性変形が始まる現象を材料の「降伏」と言う。

みなさんもゴムをビヨンビヨンしてある程度までは元に戻るけど、伸ばしすぎると（場合によっては白く濁ったような感じになり）元に戻らなくなったことがあるでしょう？あれも弾性変形と塑性変形（白く濁った部分が塑性変形）の一種です。

さて、降伏以降の挙動をさきほど見せた応力ーひずみ線図の上に描くと、塑性変形は下図のような感じになる。見ての通り、こうなるともはや比例関係ではなくなっていることが分かるだろう。比例ってのはグラフ上で直線関係になることだからだ。

すなわち、材料が降伏して、塑性変形が始まるとフックの法則は成り立たないということだ。

材料力学で扱うのは序盤の弾性範囲

さて、降伏以降どんどん変形が進むと最終的にはこの丸棒は破断してしまう。破壊に至るまでにはまた紆余曲折があるのだが、この記事ではその辺りの話はやめておこう。

とにかくここで分かってほしいのは、材料の変形序盤の変形量が小さい領域は弾性変形の範囲であり、その後塑性変形が始まると大きく変形していく、ということ。そして、フックの法則が成り立つのは弾性変形の範囲の話で、塑性変形が始まると成り立たなくなる、ということ。

このことをよく理解してほしい。

材料力学では『応力とひずみはいつもフックの法則が成り立つよ！』みたいなノリで解説されがちだが、これは材料力学が基本的に弾性変形を取り扱う学問だからだ。

なので、材料の変形と負荷の関係を表す関係式として、フックの法則が万能の法則のように感じている人も多いかもしれないが、実は違ってあくまで弾性変形している間だけだよ、ということを覚えておいてほしい。

ここで意地悪な例題

ここまで説明してきた事をより実感してもらうために、意地悪な例題を考えてみよう。

まず（１）応力を計算しよう。断面に一様に作用する引張応力は、作用している引張の内力を断面積で割れば求まるので、下のように計算できる。

では次に（２）のひずみを計算してみよう。例によってわざと間違えてみる。下はフックの法則しか頭にない人の回答例だ。

上のような計算は、この時点で即間違っているとは言い難い。なぜならこの問題の状況が、弾性変形の範囲内の話なのか、すでに塑性変形をしているのか分からないからだ（まあ実際は鉄鋼材料と書いてるから、こんなに大きく弾性変形する訳ないって分かるんだけど）。この計算結果は、『もしこの材料がこの応力まで弾性変形していると想定したら、このぐらいひずむよ』というひずみ量を表しているに過ぎない。

では、実際のひずみ量はどうやって計算しよう？

幸いこの問題では変形した結果、材料の長さがどうなったか教えてくれている。であれば、フックの法則よりも優先して、定義に基づいてひずみを計算すべきだ。

定義によるひずみの計算結果は、フックの法則により求めたひずみとは異なる値を示した（しかも、より大きな値となった）。このように、フックの法則と定義による計算結果が一致しないということは、もはや法則が破綻していることを示している。つまり、すでにこの材料は弾性変形の領域を抜け出ており、より大きな変形（つまり塑性変形）をしているということだ。

何回も言ってるけど、フックの法則が成り立つのは弾性変形の範囲だけであり、上のように定義による計算の方が優先される。この問題の場合は、変形前後の長さが与えられている訳だから、フックの法則とか最初から考えずに、定義に基づいてひずみを計算すれば良い。

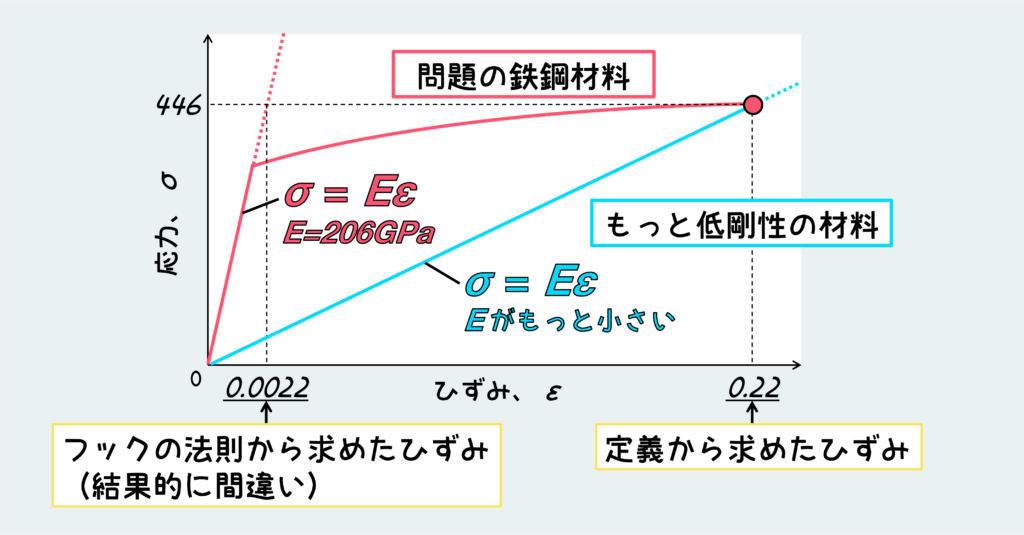
この問題の状況を「応力ーひずみ線図」に描くと下のようになる。降伏点は問題で与えられていないから、どこでグラフが折れる（降伏する、塑性変形が始まる）かは分からないけど、とにかく弾性範囲を超えて塑性変形の領域まで行ってるはずだ。

もちろんこの問題がフックの法則を用いて解ける場合もあるかもしれない。けど、その場合は金属のような剛性のある材料ではなく、大きく弾性変形するようなもっとヤング率の小さい材料が対象になるはずだ。その場合は、定義によって求めたひずみと、フックの法則から求めたひずみが一致するはずだ。（下図の青線のような材料）

上のような問題はひっかけというか、意地悪な問題の出し方をしているのだが、フックの法則や応力ーひずみ関係のことを真に理解しているかを問うには良い問題なのかもしれない。

フックの法則はあくまで弾性範囲のみ成り立つものであって、ひずみや応力の算出には定義による計算の方が優先されることをよく理解しておこう。

まとめーフックの法則は弾性変形のみ成り立つ

かなり噛み砕いて丁寧に説明してきたが、いかがだろうか？

この記事で言いたいことはただ一つ。フックの法則は決して万能の法則ではなく、弾性変形している場合のみ成り立つということだ。

意外と分かっていない人、気付いていない人もいるかと思うので、材料に応力をかけていったときにひずみがどう変化していくか、この記事でよく理解してほしい。