材料力学　応力とは？10分で完全に理解できる 基本かつ超重要な解説【材力 Vol. 2-1】

応力っていまいちよく分からなくない？

高校物理までは扱わないため、応力という概念がいまいちスッと入ってこない人は多いのではないだろうか？しかし、材力においては応力を使いこなすことこそ極意だと言ってもいい。

この記事では、応力について死ぬほど分かりやすく解説したい。材料力学を勉強していて、よく分かんないなと足踏みしている人はぜひ最後まで読んでみてほしい。10分後には、材力の基本をしっかり押さえて、さらにはマスターする準備ができているだろう。

材力ってなんのためのモノ？

材料力学を学ぶ学生のみなさんは、材力っていったい何のためのモノで、どういう風に使うの？って思う人も多いかもしれない。この疑問に簡単に答えるとしたら、こんな感じだろう。

この文章の前半部分・・つまり、力の伝わり方を把握することについては『自由体の考え方』をうまく使わないといけない。『自由体の考え方』については下の記事で以前説明したので、この記事もぜひ読んでみてほしい。

2020年10月13日 材料力学　《全員必見・超重要》自由体の考え方の基礎【Vol. 1.1】

後半部分の変形や破壊については、物体が受ける負荷の大きさの指標である『応力』を知る必要がある。応力の大きさに応じて材料は変形するし、応力が材料の持つ限界値を越えれば破壊してしまう訳だ。破壊してほしくなければ、応力が限界値よりも小さくなるように設計しないといけない。

このように材料の変形・破壊現象は応力がほぼほぼ支配しているので、応力を正しく知ることこそ材力で目指すべきことと言っていい。てことで、この記事では、応力について説明していきたい。

応力って何？

応力の意味 ー それは材料が受ける負荷の物差し

応力というのは、力を受けた物体にかかる負荷の大きさを表したものだ。負荷の大きさを表すのであれば「力」でもいいような気がするが、そういう訳にはいかない。材料にかかる負荷の大小は、単純に「力」だけで判断できないからだ。

下の絵を見てみよう。直径10 cmの鉄製丸棒と直径5 mmの同じく鉄製丸棒の両方に1 tonの車をぶらさげた状態を考えてみよう。丸棒にかかっている「力」はどちらも1000 kgf（10000 N）だけど、どうみても5 mmの丸棒の方がしんどい。

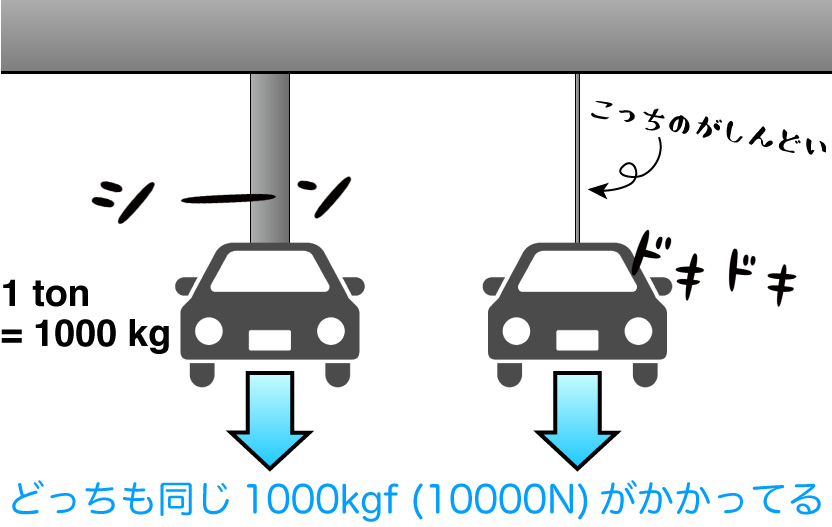
このように、同じ大きさの「力」がかかっていたとしても材料が受ける負荷は同じではない。材料が受ける負荷の大小を正しく評価するためには、「力」だけでなくその材料の「サイズ」や「断面形状」を考慮した物差しが必要になる。それが『応力』ってことだ。

つまり、応力とはサイズや形状が違う材料でも負荷の大小を比較できるようにしたもので、基本的にはある面に働いている内力をその面の面積で割ることで求められる。難しい言い方をすると、応力とは単位面積当たりの内力の大きさを表している。ここでは簡単に説明するために、面に一様に内力が働いている前提で話をしている。（曲げやねじりの場合とか、サンブナンの原理を考慮する場合とか、単純に内力を面積で割るだけでは応力を計算できない場合もある。）

ていうか内力って何よ？ていう人もいるかもしれないが、内力こそ応力を知るために重要なものだ。このことについては、次の所で詳しく説明しよう。

ちなみにこれもあとで説明するが、応力には垂直応力とせん断応力の２種類があり、垂直応力はσ（シグマ）、せん断応力はτ（タウ）で表す。応力の単位は「力」÷「面積」なので、【N/m²】とか【kgf/mm²】とかがあるが、よく使うのは【MPa】だ。【MPa】は【N/mm²】に等しいことを知っておくと便利だ。どんな風に便利かは以下の記事を参考にしてほしい。

2018年7月25日 材料力学　公式を正しく使い、計算ミスを減らすコツ【材力 Vol. 0.3】

内力が重要！

材料のどこにどんな応力が働くかを決定しているのは内力だ。なので、応力を知るためには、内力を把握することが必要だ。まず外力と内力について、ちゃんと違いを理解しよう。

まあ言葉で説明するよりも具体例を見た方が良いだろう。

下の図のような棒状の材料ACがあり、これの中間地点Bのところに図のように荷重をかける。この荷重”P”が『外力』という訳だ。

左側だけを固定しているケース(a)と両端を固定しているケース(b)の２つの場合で、それぞれの材料に働く内力および応力を考えよう。

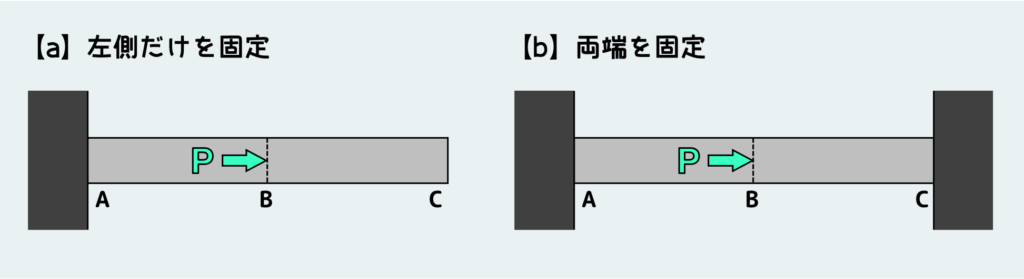
材料内部にどう力が伝わるか、つまり内力を知るためには材料を仮想的に切断して、自由体として取り出す必要がある。切断してはじめてその切った面に働く内力を知ることができるわけだ。AB間・BC間に働く内力を知るために、AB間のどこかとBC間のどこかで切断して、自由体図を描いてみよう。

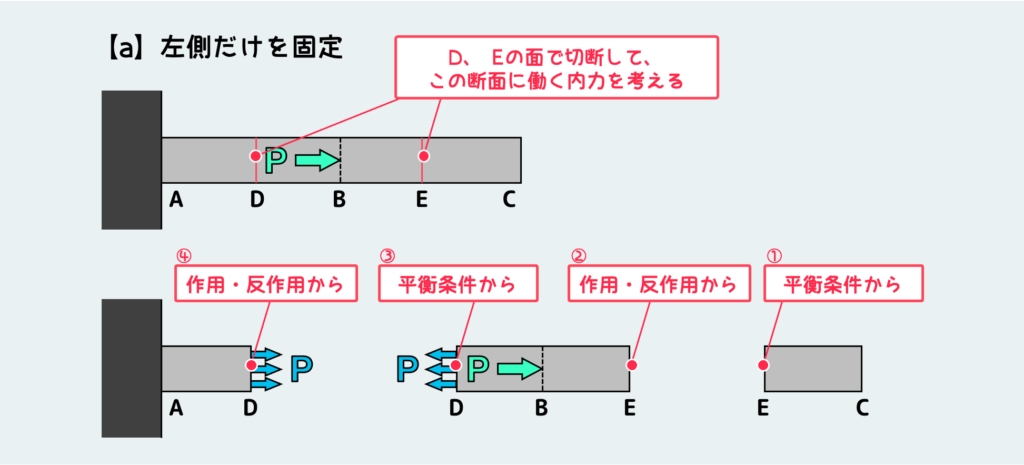
まずケース（a）では、自由体の平衡条件と作用・反作用の法則から、切断した面に作用する内力は下図のように決定できる（図中の①〜④は思考の流れ）。この自由体図はAB間・BC間の任意の場所で切ったときの絵だが、切る場所がその区間内の別の場所に変わったとしても出来上がる自由体図に変化はない。つまりAB間はどこを見ても引張の内力Pが作用しており、BC間はどこを見ても内力は働いていないということがわかる。

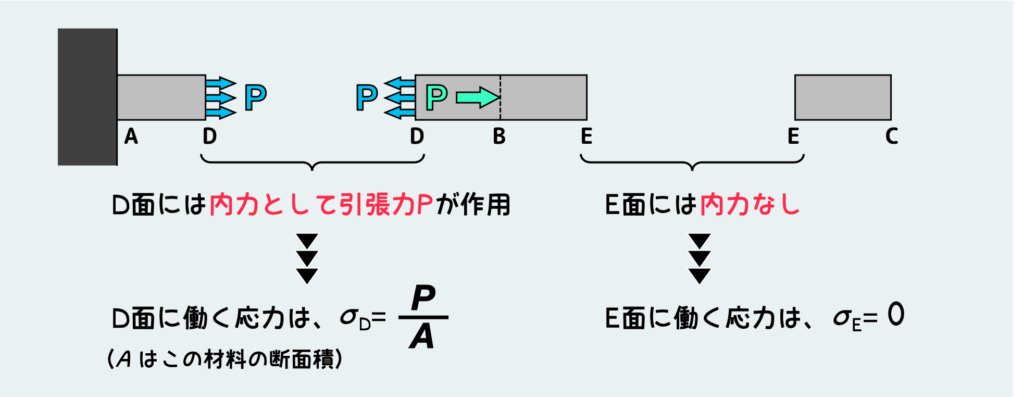
このように内力が把握できれば、そこに働く応力が決定できる。すなわち、内力Pが伝わるAB間ではどこの断面にも引張応力P/Aが作用しており、一方BC間には内力が働いていないので、どこの断面を見ても応力も同様に働いていない。

さて、では次にケース（b）ではどうか？やり方は同じで、AB間・BC間の適当なところで切断して自由体図を描いてみる。この問題の場合は、自由体の平衡条件を考えるだけでは内力が決定できないのだが（不静定問題）、ここではその事は横に置いておこう。平衡条件と変形の条件からAB間およびBC間に働く内力が下図のように決定できたとしよう。

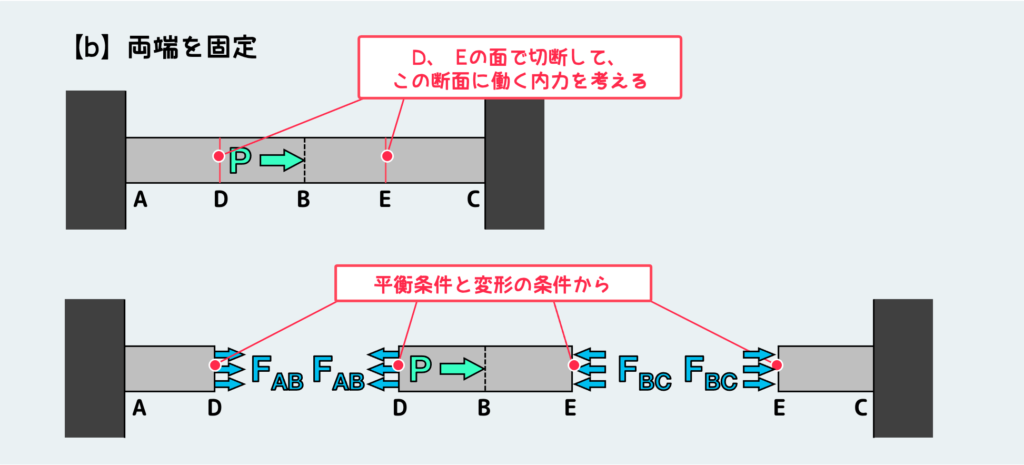
そうすると、AB間では引張の内力F_ABが働いているので、AB間のどの断面にも引張応力F_AB/Aが働く。BC間には圧縮の内力F_BCが働いており、BC間には圧縮応力F_BC/Aが働いているということになる。

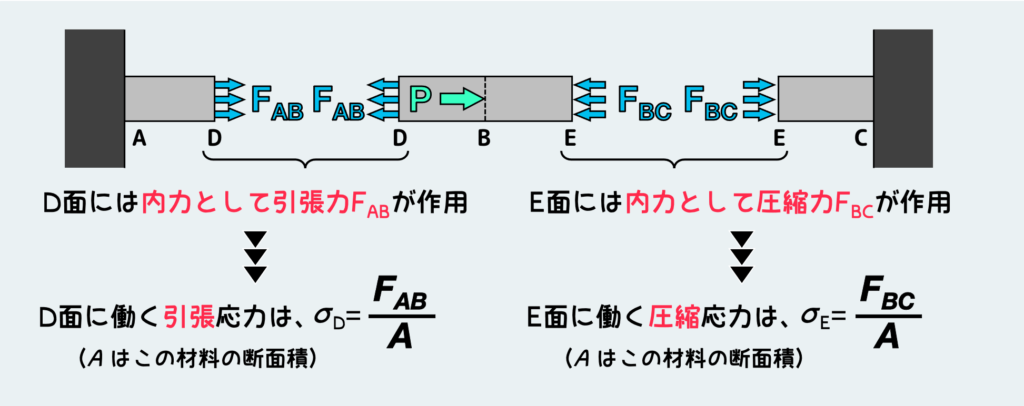
この２つのケースでは、外力として加わっている力はどちらも同じPという力である。しかし、条件が異なれば各部分に働く内力は当然異なり、これに応じてそこに働く応力も異なる。

以上のように、ある場所に働く応力はその場所に働く内力によって決定される。

ということをよーく理解してほしい。

モノを安全に設計するために応力が必要！

おおざっぱに応力のことが分かったところで、実際どんな風に応力を使うのか見てみよう。主な使い方としては、安全設計のために使ったり、安全か危険かの判断のために使ったり、といった感じだろう。

やることはシンプルだ。材料に作用する応力とその材料の耐えられる限界値を比較して、限界突破したらダメ、限界以下に抑えられたらOK。これだけだ。

材料に作用する応力は、上で説明した通り内力を元に計算できる。例えば単純に引張荷重を受ける棒の場合は、外力と等しい大きさの引張力が内力として働くので、これを断面積で割れば応力が得られる。

一方、材料の耐えられる限界値は材質によってだいたい決まっていて、規格等で定められている。限界値にはいくつかの種類があり、どの限界値を使うべきかは「どういう現象まで許せて、どういう現象が許せないか」によって決まる。

とにかく破断しなければ良い、という状況であれば引張強さ（破断強さ）を超えないように設計すれば良い。しかし、大きな変形をすることすら許されない状況（ふつうはこっちだろう）であれば、降伏応力（もしくは耐力）を限界値として採用しなくてはならない。

まあ実際は、限界値ギリギリの応力がかかるような設計にはしないので、安全率をかけることで破断強さや降伏応力よりも何倍も低い値を許容応力として設定するのが普通だ。

（長期間何度も何度も負荷を受けるようなモノの設計のためには金属疲労を考慮しなくてはいけないけど、そこまで話すとだいぶややこしくなるので、ここでは疲労のことは無視して話をしている。）

安全な設計とはつまり、簡単に言うと以下のようなことだ。

安全設計の方向性としては上の通りだが、実際には色んな制約が付く。サイズをある大きさ以下に抑えないといけないとか、高強度材にすると加工が難しくなるとか、コストカットしないといけないとか、そういう制約だ。場合によっては見栄えを良くしたいとかもあるかもしれない。

安全性とこれらの制約を両方満足するようにすることこそ、工学者の使命だ。

応力の種類（引張・圧縮・せん断）

応力には上でも言った通り、垂直応力とせん断応力の２種類がある。垂直応力の中にはさらに引張応力と圧縮応力の２種がある。

垂直応力は、ある面に対して垂直な方向に働く内力をもとにした応力で、内力が引張力であれば引張応力に、圧縮力であれば圧縮応力になる。垂直応力が働いた結果、材料はその方向に伸びたり、縮んだりするような変形を起こす。日常生活でいわゆる「力」と言えば、このような面に対して垂直に働く力を指すので、垂直応力についてはとてもイメージしやすいと思う。

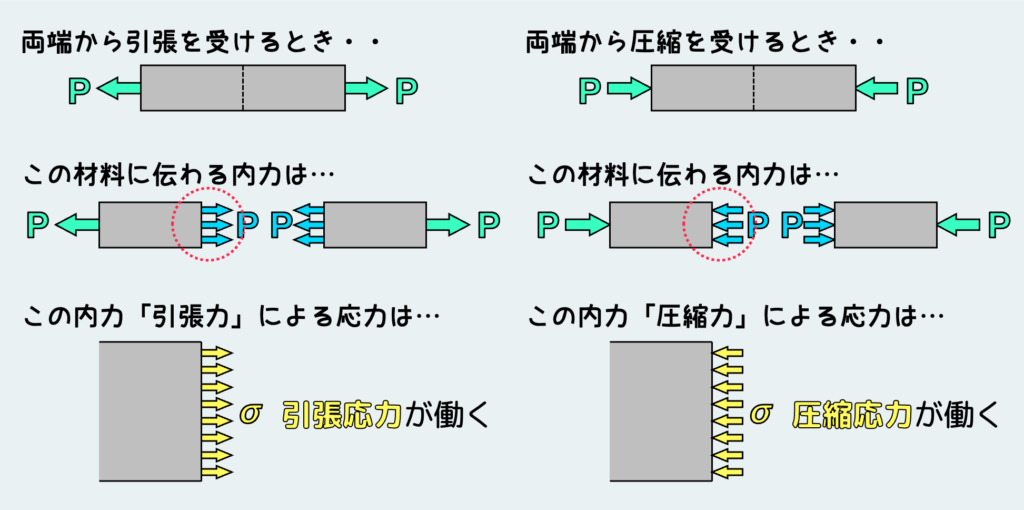
また、内力が曲げモーメントのときもその面に働く応力は垂直応力になるが、この場合は少し特殊で、引張応力と圧縮応力が混在した形になる。詳しくは「曲げ」のトピックのときに説明したいと思うが、一例だけ見てみよう。

「曲げ」でよく扱うのは「はりの曲げ問題」である。「はり」とは建築物なんかで、水平方向に渡ってる部材のことで、一方縦にたってる部材のことを「柱」という。すごく簡単な例として、先端に荷重を受ける片持ちばりの例を考えよう。図のように先端に外力として力を受けたはりの途中の断面には、内力としてせん断力と曲げモーメントが働くことになる。（※この面には当然せん断力によるせん断応力も働くのだが、曲げ問題におけるせん断応力は曲げモーメントによって発生する応力よりもすごく小さくなることが多く、あまり重要ではない。ここではこのせん断応力の存在を無視して話を進める。）

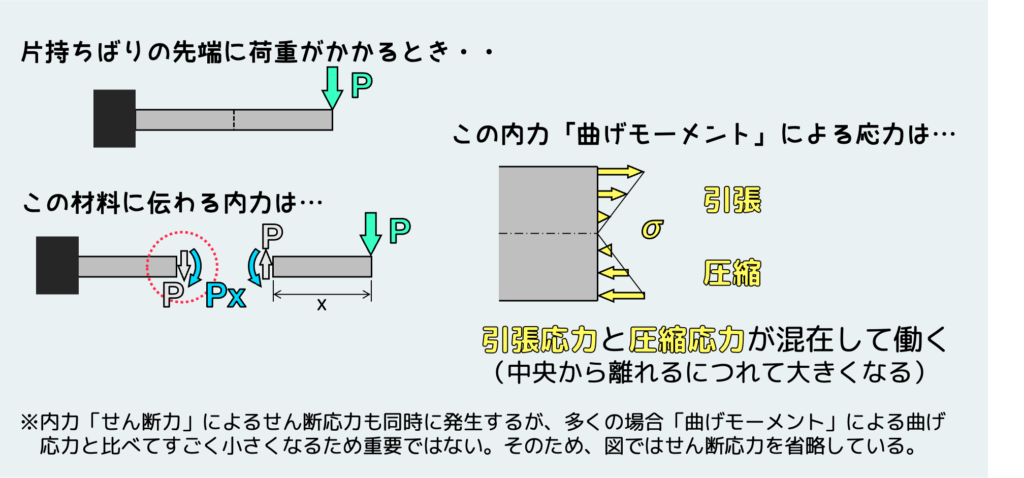
この曲げモーメントが働いている面の応力はどうなっているかというと、上半分は引張応力、下半分は圧縮応力になっている。もう少し詳しく言うと、中央部の応力は ”0” で、中央から離れるに連れて応力の絶対値は大きくなっていく。実際に何か材料を曲げてみると分かると思うが、上半分は伸びようとするのに対し、下半分は縮もうとすることがイメージできるだろう。しかも、中心部から離れるほど大きく変形しようとする。こういう現象を起こしているのが、上で説明したような特殊な応力分布な訳だ。こういう風な曲げによって起こる引張応力と圧縮応力が混在した形を「曲げ応力」と呼ぶ。

一方、せん断応力については、少し取っ付きにくいと感じるかもしれない。引張応力や圧縮応力がある面に働く引張や圧縮の内力に起因していことと同じで、せん断応力はせん断の内力（今後”せん断力”と呼ぶ）に起因するものである。せん断力はある面に対してその面に沿った方向に働く内力であり、せん断応力も当然同じように面に沿った方向に働く。

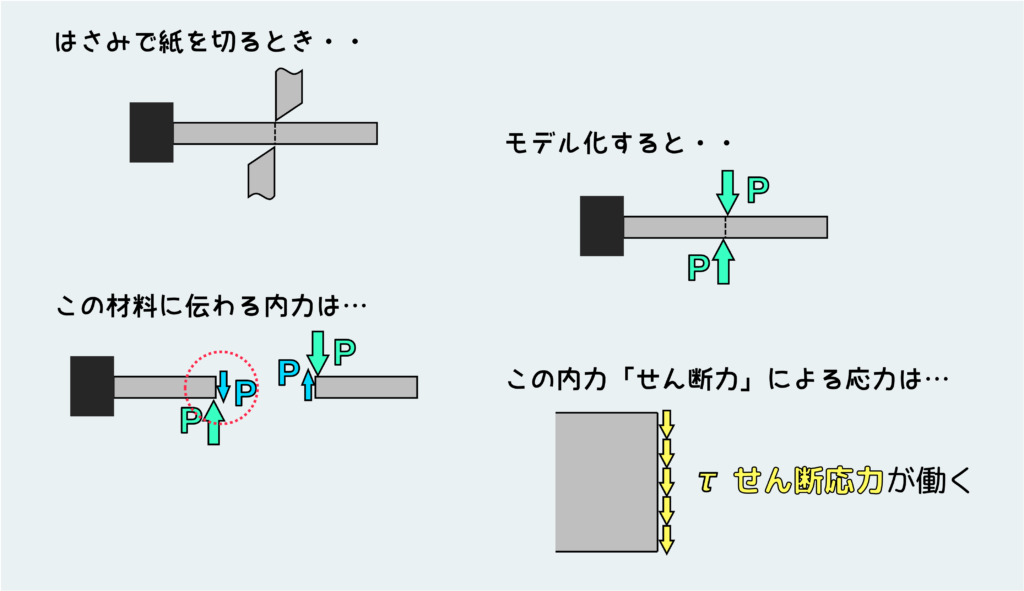
一番身近なところでせん断力およびせん断応力が登場するシーンといえば、はさみで紙を切るときだろう。はさみで紙を切るときの状態をモデル化して描くと図のようになる。はさみで切断される面（刃と刃の境目の面）には図のように応力が働き、これがせん断応力な訳だ。

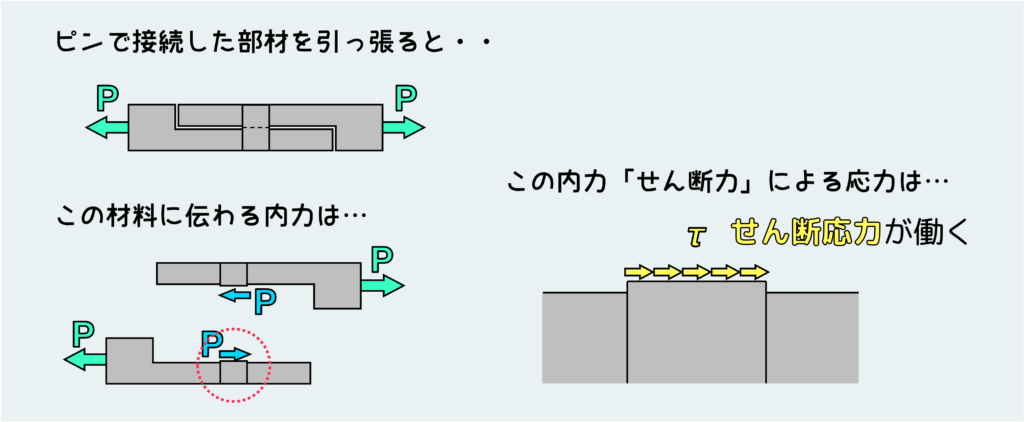
もっと工学的な例を出すとすれば、部材同士を接合するリベットやピンに作用するのもせん断応力だ。

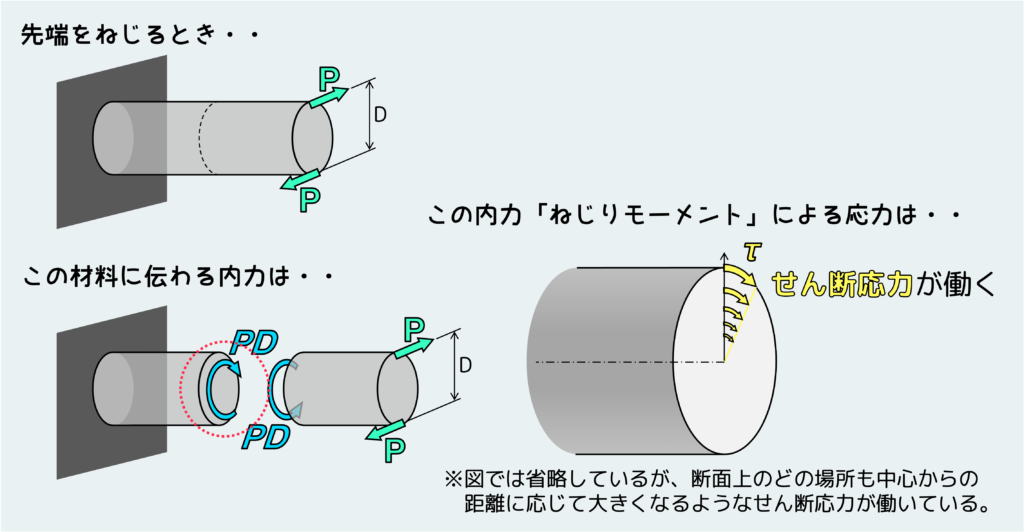
また、せん断応力が登場するもう一つ主要な形態として「ねじり」がある。ねじりを受ける棒の場合、内力として働くのはねじりモーメント（トルク）である。トルクによって発生するせん断応力は「曲げ」のときと同じくある勾配を持った分布となる。つまり「曲げ」のときと考え方は同じで、中心部は変形しないのに対し、表面付近は大きく変形しようとする。そのため、中心部の応力は ”0” であり、中心から離れるに連れて大きくなるようなせん断応力分布となる訳だ。

微小要素での表現

最後に微小な要素に対して応力を描くときを確認しよう。

垂直応力（引張応力と圧縮応力）については簡単だ。垂直応力が働いている部分から微小な要素を取り出してくると、その応力状態は下図のように描ける。つまり、元になっている内力（引張力と圧縮力）の方向に合うように、要素の両側に応力を描き込むだけで良い。垂直応力場にある微小要素には、相対する２面に同じ大きさの引張応力や圧縮応力が作用するだけってことだ。

一方、せん断応力には垂直応力と違う特徴があり、注意が必要だ。理解すべきことはずばり『せん断応力は必ず４面に対をなして働く』ことだ。このことを理解するために、さっきのはさみで紙を切る例をもう一度見てみよう。

はさみで切る面を自由体として取り出してきて、この面に働くせん断応力を描き込むのであれば、４面に働くとか考えずに下図のように描き込んで良い。切断した面以外（自由表面）に応力や内力を描き込むことはできないので、今描けるせん断応力は図で描いた部分だけで、これが外力としてはさみから加えられる力と釣り合っている。

ここから微小な要素を取り出してくると、せん断応力の特徴が見えてくる。さっきの自由体のときと共通する面（右側の面）には、当然自由体図のときと同じせん断応力が働く。で、垂直応力のときと同じように反対側の面に反対向きのせん断応力が働くのは容易に想像できるだろう。これで微小要素に作用するせん断応力状態として十分だろうか？

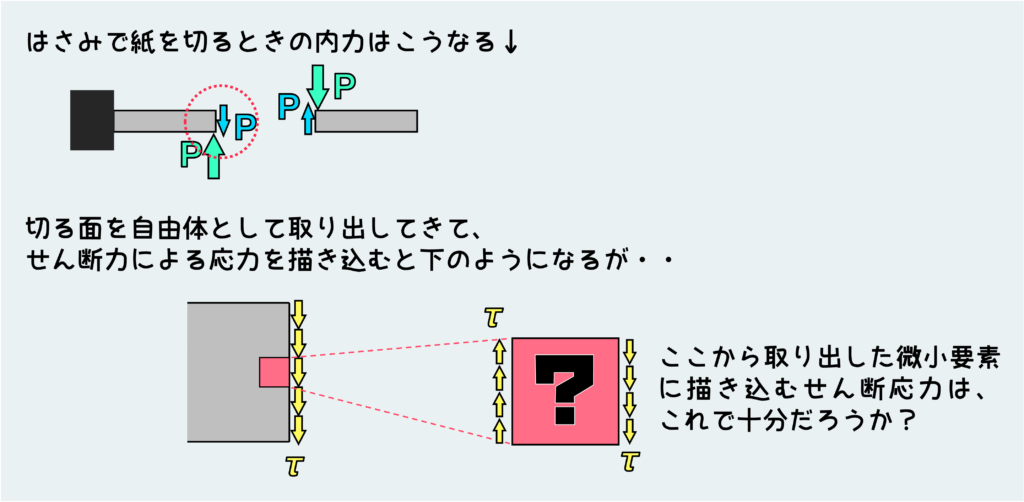
いやいや、これでは足りない！なぜかと言うと、微小要素だって平衡条件を満足する必要があるからだ。このままだとこの要素は回転してしまう！

じゃあ平衡条件を満たすためにどうなるべきか考えよう。他の２面も元々隣り合う材料と繋がっていた面なので、応力が働いても問題ない。回転を抑えるためには上下の面に図のような応力が働かないといけない。この状態なら微小要素の「力の釣り合い」と「回転の釣り合い」を同時に満足させることができる。

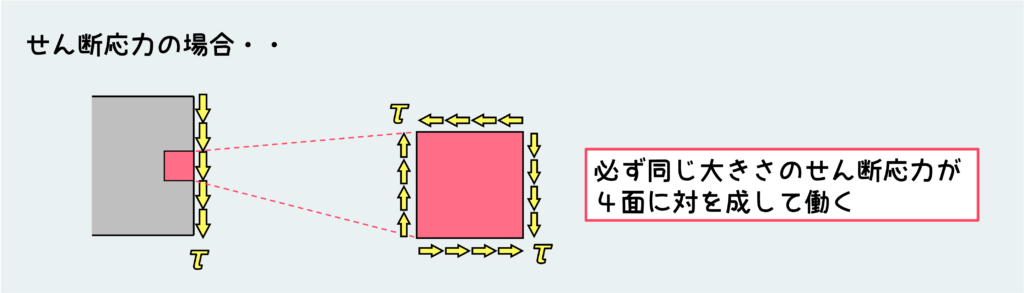
という訳で、せん断応力が働く微小要素を考えるとき、図のように必ず同じ大きさのせん断応力が４面に対を成して働いていなければならない。これはせん断応力の非常に重要な特徴なので、しっかりと理解しておこう。

ちなみに、ねじりの場合の説明はここでは省略するが、ねじりを受ける材料から取り出してきた微小要素も同様なせん断応力状態（４面に同じ大きさのせん断応力が働く）となっていなくてはならない。

まとめ

とっても簡単で分かりやすく応力について解説してきたつもりだが、どうだったろうか？

応力という材料力学を使いこなすために必要不可欠なものが少しでも理解してもらえたら嬉しく思う。