材料力学や材料強度試験でよく登場する『降伏』というワードについて、3分でサラッと解説していきたいと思います。
降伏点って何？どうやって求めるの？などなど基本的な疑問を抱えてる人は、簡単に要点がつかめますのでぜひ読んでみてください！
夢へ駆ける少女の姿に感涙！！
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか？」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい！」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanならなんと3巻まで無料で読めてしまいます！まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです！
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
降伏点とは？
材料を引っ張ると、変形の初期では負荷の大きさに比例して変形していきます。すなわち『応力』と『ひずみ』が比例関係にあり、この時点の材料は負荷を取り除くと元の大きさに戻ります。こういう変形挙動を『弾性変形』といいます。
その後さらに引っ張っていくと、突然大きく変形が進みはじめます。こうなると、もはや材料は負荷を取り除いたとしても元の大きさには戻れず、変形が残ってしまいます。こういう変形を『塑性変形』と言い、負荷を取り除いたあとに残る変形のことを『塑性ひずみ』とか『永久ひずみ』とか言います。
このように材料が弾性変形の限界を迎えて、塑性変形に移行する現象のことを『降伏』と言い、そのときの限界の応力のことを『降伏点』と言うわけです。材料が「もうだめだぁ」となってしまうってことです。面白いネーミングですよね。
記号は普通σy（シグマワイ）を使い、単位は普通【MPa】です。英語では【yield stress・イールドストレス】と言います。
下の絵は、鉄鋼材料の典型的な応力ひずみ曲線です。応力ひずみ曲線というのは、材料の引張試験をしたときに得られる応力とひずみの関係をグラフに描いたものです。
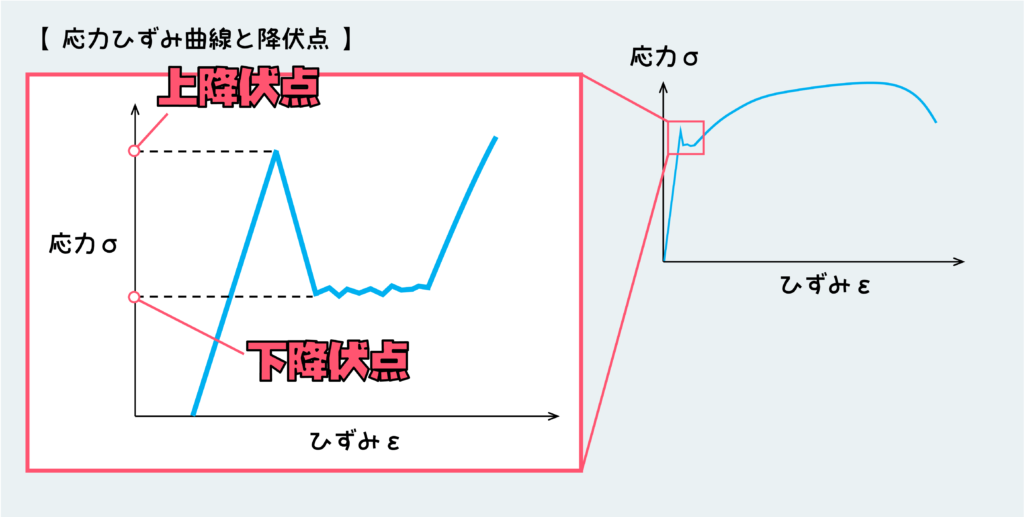
図の中で、原点から直線で伸びている部分が弾性変形の範囲です。見ての通り、応力とひずみが比例関係にあるのが分かります。その後ある点で応力がガクッと落ちて、応力があまり変化せずにひずみだけが大きくなるウロウロした区間があります。
このガクッと落ちる点で起きている現象が『降伏』です。ちなみにこのガクッと落ちる点の応力を『上降伏点』と言い、その後のひずみだけがだらだら大きくなる領域の応力を『下降伏点』と言います。
降伏点は引張試験によって求めます。引張試験では、材料にかけている荷重の大きさと変形量を測定します。測定した荷重を試験片断面積で割ることで引張応力が求まります。また、伸び（変形量）を初期の試験片長さ（標点間距離といいます）で割ることでひずみが求まります。
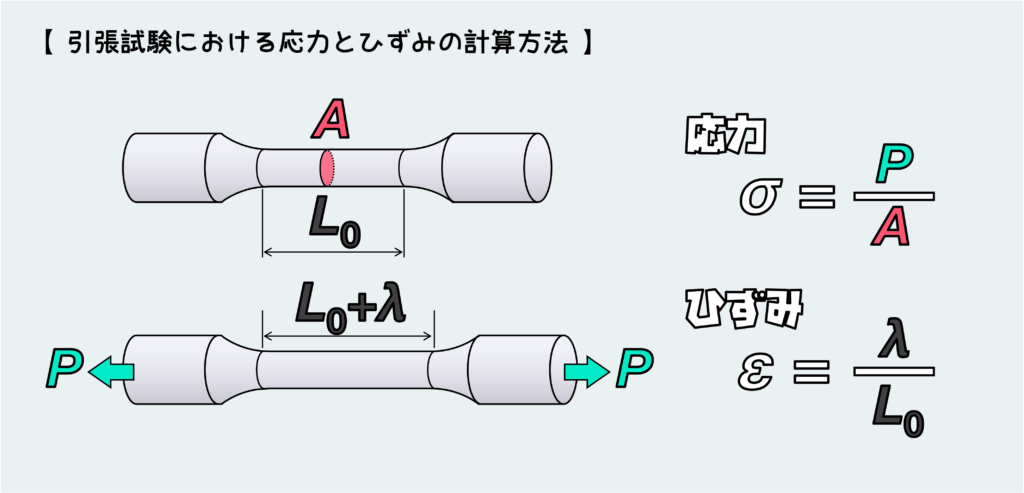
これらをグラフ用紙にプロットすることで応力ひずみ曲線が得られます。
降伏点を知るためには、描いたグラフからさきほど説明した上降伏点や下降伏点に当たる点の応力を抜き出せば良いわけです。
実は今回説明したような、ガクッと突然塑性変形が始まる『降伏』という現象はすべての材料で出現する訳ではありません。というより、炭素鋼のような限られた材料でのみ見ることができる現象です。
その他の金属材料でも弾性変形から塑性変形の移行はもちろん起きますが、炭素鋼で起きるような降伏と比べてもっとゆるやかに起きます。
このような材料では、明確な弾性変形の限界の応力が定義しにくいため降伏点ではなく『耐力』というものを採用します。これについては別の記事で説明したいと思います。
関連する記事
さらに詳しく関連する内容について学習したい人は以下の記事を読んでみてください。
引張応力とは？求め方や引張応力による変形・ひずみの考え方を徹底解説【材力Vol. 3-1】
【マンガ】金属の引張試験を人間に例えてみた
【3分で解説】弾性変形とは？塑性変形との違い、どれくらいの大きさ？応力ひずみ曲線との関係
【3分で解説】耐力とは？降伏点がない材料って？降伏応力と耐力の違いをササっと解説！
研究者を志す者 必読！！
全8巻完結
こんなにも知的探究心を刺激される漫画があったとは！
真理のために命をかけた先人たちの物語。
この作品は、現役研究者である私・ぽるこが衝撃を受けた作品として、特に研究者およびこれを志す者には強く本気でオススメします。今ある常識を疑う心、誰に何を言われようと真理を追求する姿勢に触れ、心が動くこと間違いありません。
私自身、世界のトップ研究者だった師匠によく言われた言葉を思い出します。“目の前の現象に楽な答えを持ち出し、疑うことをやめ、真理の追求という困難な道から逃げていないか！？”
本作はこういった研究者の気概なるものを感じる、必読の価値ある一冊です。全8巻ですでに完結していますし比較的手軽に一気読みできます。気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！