前回までの記事で、はりの曲げ問題のSFD、BMDの考え方、そして応力について説明してきた。これらを踏まえた上で、この記事では曲げの微分方程式について解説していきたい。

微分方程式って難しそうだし、何のためにやるの?

曲げを受けるはりの変形の様子を知るためのもので、コツをつかめばそんなに難しくないよ!
微分方程式を解くことで、曲げを受けるはりの変形の様子の全体像を把握することができる。方程式自体は全然難しくない。最も重要なことは境界条件が何かを見極めることだ。
微分方程式って聞くだけで苦手な印象を受ける人も、この記事を読み終わった後はやり方が分かるはずなので、ぜひ読んでみてほしい。
- 手順は以下の通りで、最も大事なことは境界条件を正しく見極めること。
- まずは、BMDのときと同じように、はり中に伝わる曲げモーメントを位置xの関数として表現すること。
- 1つの曲げモーメントにつき1つの微分方程式を作り、これを2回積分して、積分定数が2つ出てくる。
- 境界条件を元に積分定数を決定する。
- 境界条件は支点の位置で設定する。場合分けがあるときは、場合分けの境目でもはりがつながっていることを利用して設定する。
夢へ駆ける少女の姿に感涙!!
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか?」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい!」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanならなんと3巻まで無料で読めてしまいます!まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです!
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!
Contents
曲げの微分方程式を解くことで何が分かる?
まず、微分方程式を解く目的ってのをはっきりさせておこう。
微分方程式には、あるxの位置におけるはりのたわみw(x)と、あるxの位置における断面に働く曲げモーメントM(x)が登場する。どちらも位置xに依存する量なので、xの関数として表される。
微分方程式を解くというのはつまり、このたわみw(x)の中身、どんなxの関数で表されるかを明らかにすることだ。
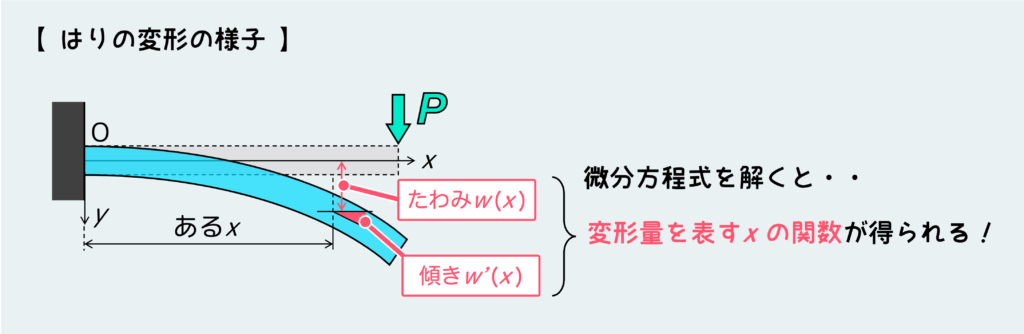
w(x)がどんな関数かが分かれば、自分の知りたい場所のxの値を関数に入れることで、その位置でどれだけはりがたわむかを数値的に知ることができる。なんだったら関数なので、グラフ用紙にその関数が表す曲線を描けば、それがそのまま変形後のはりの形になるので、視覚的に変形後の様子を理解できるわけだ。
ちなみに微分方程式を解く過程でw'(x)というw(x)の一階微分も求めることができるが、これははりのその位置における傾きを表している。(高校数学で学習したように、ある関数の微分は、その関数で表された曲線の傾きを表していることを思い出そう。)
曲げの微分方程式の解き方
では、具体的な微分方程式の解き方を見ていこう。この手順に沿って解いていけば何も恐れることはない。
まず曲げの微分方程式がどんな形で書けるかを確認しておこう。材料に曲げモーメントが働くときの微分方程式は下のように表せる。
“EI”は曲げ剛性と呼ばれるもので、材質によって決まるヤング率(縦弾性係数)と断面形状によって決まる断面二次モーメントだ。w(x)はあるxの位置におけるたわみ、M(x)はあるxの位置の断面に働く曲げモーメントだ。
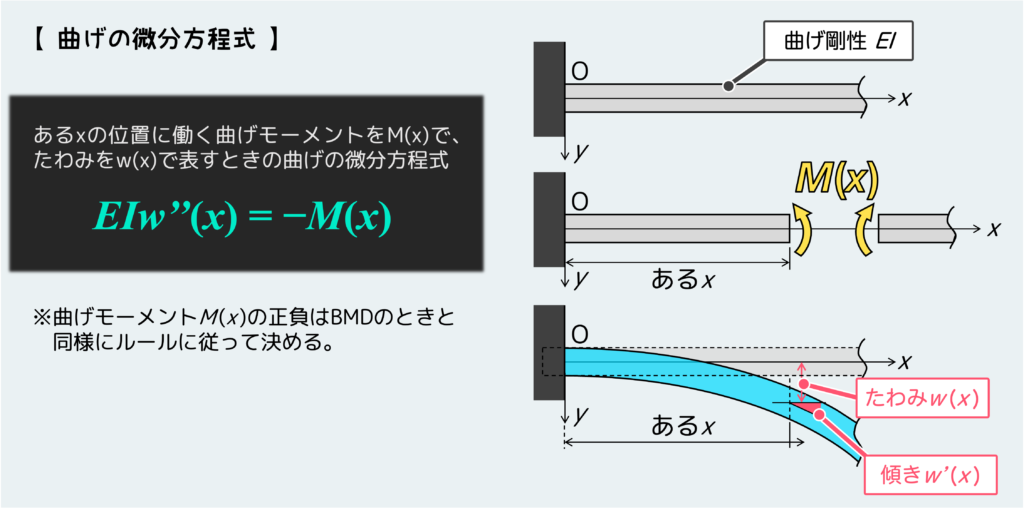
ここで注意しておくべきことは、座標の取り方とたわみw(x)や曲げモーメントM(x)の正負の定義についてだ。あくまで上の絵で描いたような取り方をすれば微分方程式は上のように書くことができて、求まるw(x)は図のy軸方向のたわみを表すことになる。
基本的にはBMDのときと同じように正負の向きを定義すれば良いが、この辺の定義は教科書によっても教える人によっても違ったりするので、よく自分の講義ではどう説明されているか確認してほしい。(場合によっては、微分方程式の右辺でマイナスが付かないように定義する教科書や先生もいるかもしれない)

基本的な解き方は、この微分方程式の両辺を積分していくだけだ。
1回積分すると傾きw'(x)に関する式になり、2回積分するとたわみw(x)に関する式となる。積分していくと、上のように積分定数が出てくるが、2回積分するので1つの微分方程式につき2個の積分定数を決定する必要が出てくる。
積分定数をどうやって決定すればいいかというと、境界条件を使う。ここがこのテーマの中で最も重要なところだ。
境界条件っていうのはつまり、この材料が置かれている状況の中で『ここだけは絶対こうなる』っていう条件のことだ。
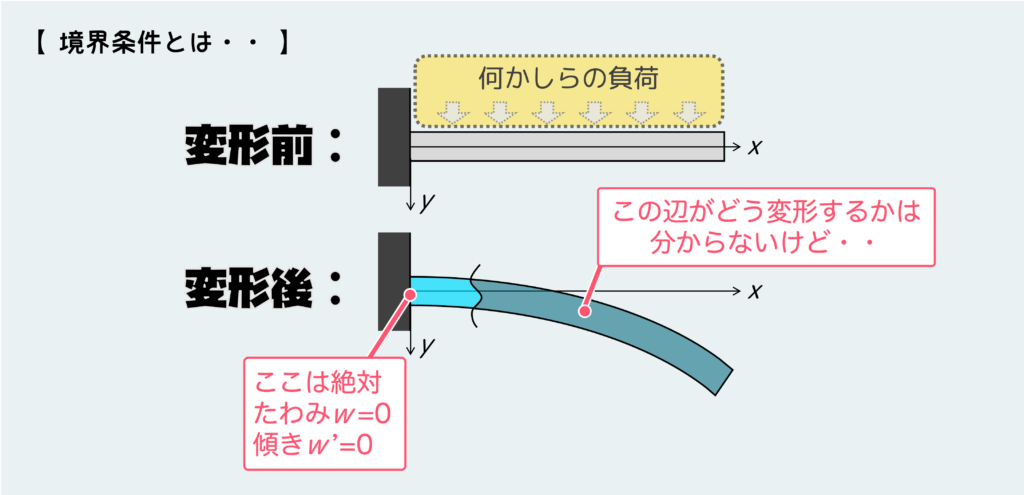
例えば上のように固定支持の片持ちばりの問題の場合は、はりにどんな負荷がかかっていたとしても壁にくっついてる点(x=0)では絶対に”たわみ”と”傾き”は “0” になる。これが境界条件となる。
その他の位置(はりの途中の部分)の変位についてはどうなるか分からない(それこそ微分方程式を解いてみないと分からない)。
微分方程式はそこまで複雑な形にはあまりならないので、積分していくこと自体はそんなに難しくない。なので、微分方程式を正しく解けるかどうかは『いかに正しく境界条件を見極めるか』にかかっていると言っても過言ではない。
境界条件を見極めるには慣れが必要かもしれないが、多くの場合いくつかのパターンのいずれかにはまってしまうので、そのパターンさえ押さえておけばそこまで構える必要はない。
境界条件を正しく見極めることができたとして、具体的にはどう使うのか。
境界条件が例えばさっきの例のように「x=0の位置でたわみが0」というようになったとしよう。これを式で表すとw(0)=0となる。
すなわち、微分方程式を解く中で出てきたw(x)に関する式に対して、x=0を代入してこのときのw(x)=0として式を整理すれば良い。そうすると、積分定数C1およびC2に関する式が得られることになる。もう1つ条件式があれば、積分定数に関する式がもう1つ得られ、これらの連立方程式を解くことでC1およびC2が決定できるという訳だ。
1つの微分方程式につき積分定数は2個出てくるので、これらを決定するためには境界条件が2個必要になる。
境界条件の見極め方
境界条件の設定の仕方はそんなに多くない。基本的には、支点での変形量(たわみ、傾き)で定義できる。シンプルな問題ではこれがほとんどだと思う。
もう一つのパターンとして、場合分けが必要なときに、場合分けの境目においてもはりがつながっていることを利用して設定する。これについてはイメージがつきにくいだろうから、具体例を見ながら理解してほしい。
1つ目は、支点で設定できる境界条件だ。支持の方法によって使える条件が変わるので、支持方法の特徴をしっかり理解しておかなければならない。代表的な支持方法とそれによって生まれる境界条件を紹介していこう。
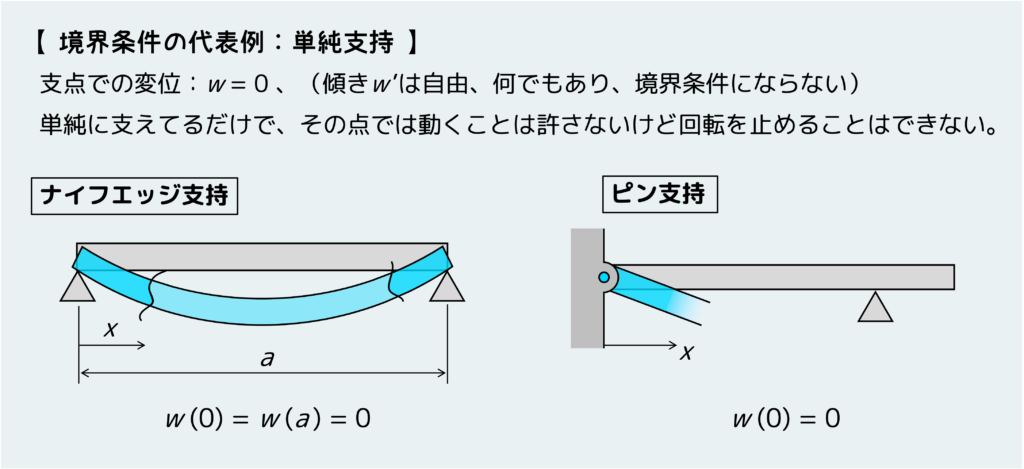
まず単純支持の場合についてだ。単純支持の特徴は回転を拘束しないことだ。なので、その位置においてたわみw(x)が0という境界条件を設定することができるが、傾きw'(x)に関しては条件設定することはできない(どんな傾きになるか分からない)。
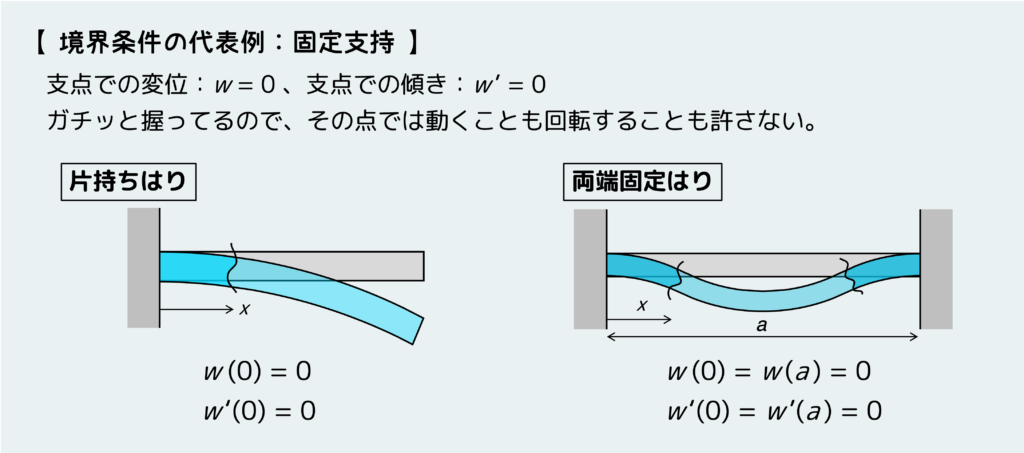
次に固定支持の場合だ。単純支持に対してさらに回転すら許さないように固定したのが固定支持だ。すなわち、固定支持している位置においてはたわみw(x)も傾きw'(x)も両方とも0になり、これらが境界条件として使えることになる。
はりの途中で状況が変化しているときには場合分けの必要が出てくる。BMDの考え方を思い出してほしいが、状況が変化する点を境にして曲げモーメントM(x)を表す式が変わってしまうので、それに伴い微分方程式も式の中身が変化することになる。
微分方程式が2つになると、当然だけど積分定数は4つになる。てことは境界条件も4つ必要になる。

4つも!?4つも支点ないし、そんなに条件見つけられるの?

支点以外にも使えるポイントがあるよ!場合分けの境目になってる点だよ!
てことでここからは具体例を見ながら説明しよう。
下のような問題が、よくありそうな場合分けが必要なケースだ。これを見ながら、微分方程式における場合分けの扱い方をマスターしよう。
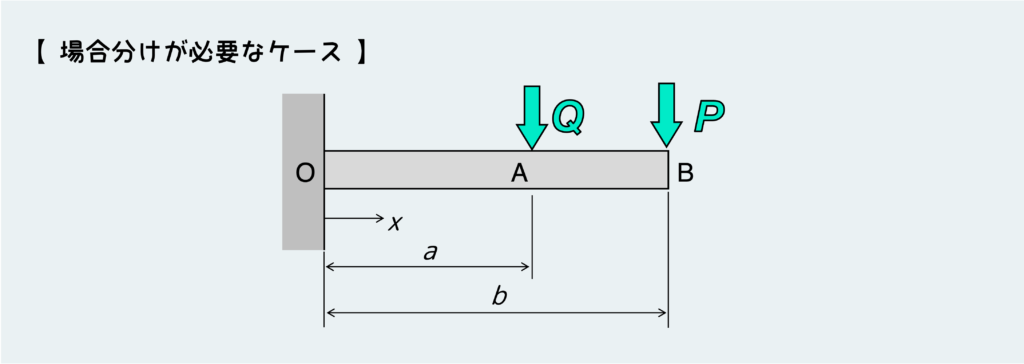
微分方程式を作るためには、あるxの位置における曲げモーメントをxの関数として表現しなければならない。これを考えるときには、SFD・BMDの考え方の所で説明したように、途中で状況が変わるようなポイントでは場合分けする必要がある。
今回の例ではA点において外力が加わっているので、A点を境にして2パターン考えることになる。つまり、A点の左右で曲げモーメントM(x)を表すxの関数の形が変わるということだ。
そうすると、当然出来上がる微分方程式の形も変わってしまうので、下のように2パターンの微分方程式ができる。このとき、xの関数であるたわみwと曲げモーメントMについてはしっかり添字(1と2)をつけて区別しておくことが大事だ。
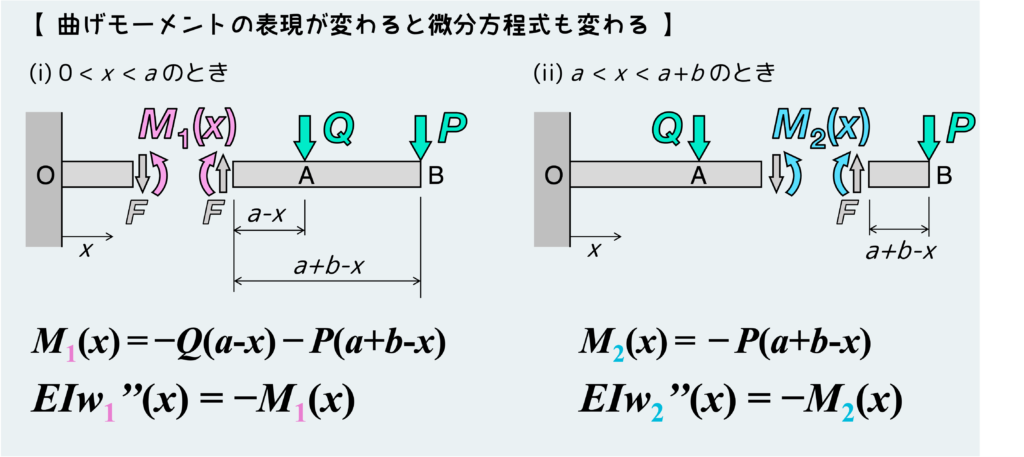
2つの微分方程式を解くということは、上でも言った通り積分定数4つを決めなくちゃいけないので、境界条件が全部で4つ必要になる。
まず1つ目の区間(0 < x < a)のときに関しては、何も難しくない。場合分けがなかったときと同様に、支点に基づく境界条件を適用すれば良いだけだ。
つまり、下のように x=0 のときにたわみwも傾きw’も0になるというのが境界条件で、これを区間1の微分方程式に対して適用して、積分定数を決定できる。
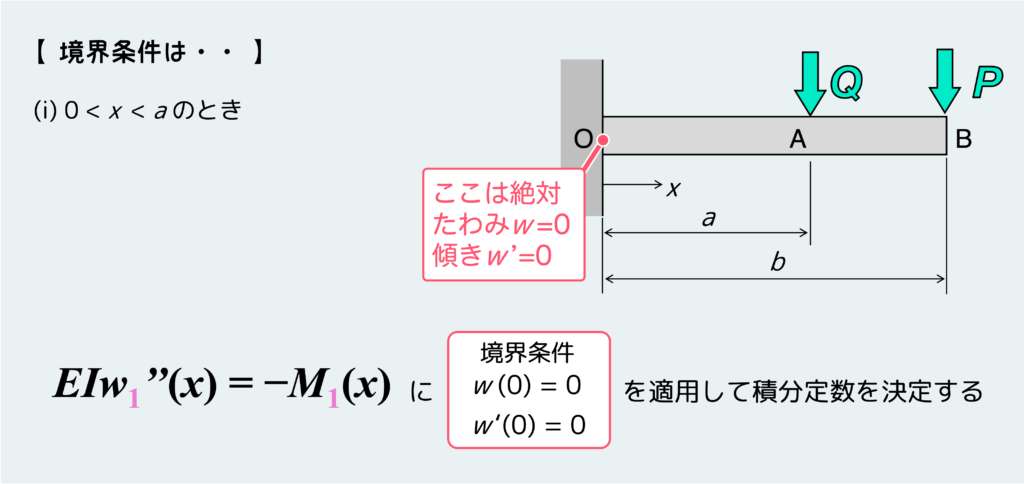
一方、区間2(a < x < a+b)の場合は支点が存在しないので、支持条件に基づく境界条件を設定することができない。じゃあ、どうすればいいだろうか?
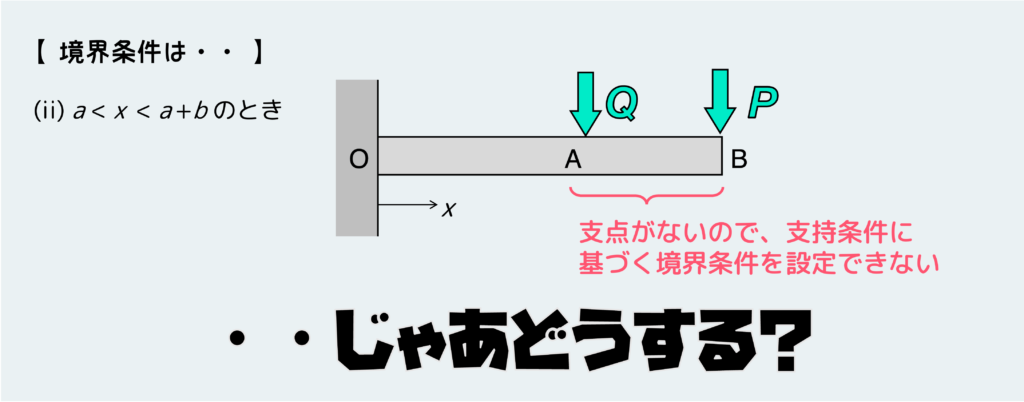
こんな場合は、場合分けの境目(今回はA点)でもはりがなめらかにつながってることを利用する。
A点を境にして変形状態を支配する微分方程式が違う、つまりA点の左側の変形状態はw1およびw’1で表現されていて、A点の右側の変形状態はw2およびw’2で表現されている訳だが、A点の状態はどっちの式でも表現することができる。
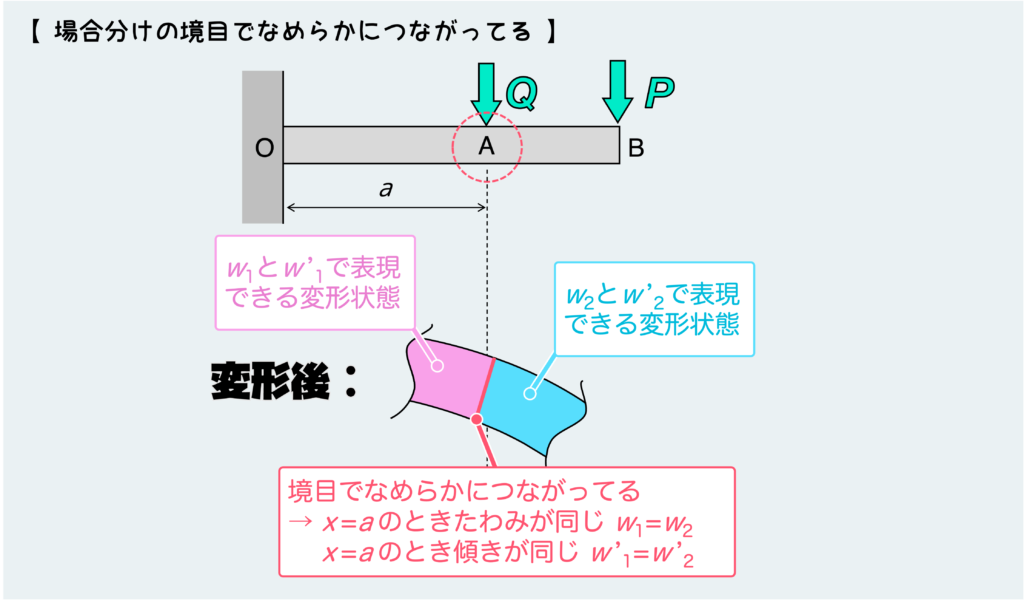
そうは言っても、変形後も材料はA点でなめらかにつながっていないといけないので、A点においてたわみw1とw2は等しくないといけないし、傾きw’1とw’2も等しくないといけない。
もしA点においてw1とw2が等しくないとしたら、たわみ量が違うことになっちゃうので下のように千切れた状態になってることを示し、w’1とw’2が等しくないとしたら傾きが急に変わることを意味するので、ボキッと折れたような状態になってることになってしまう。
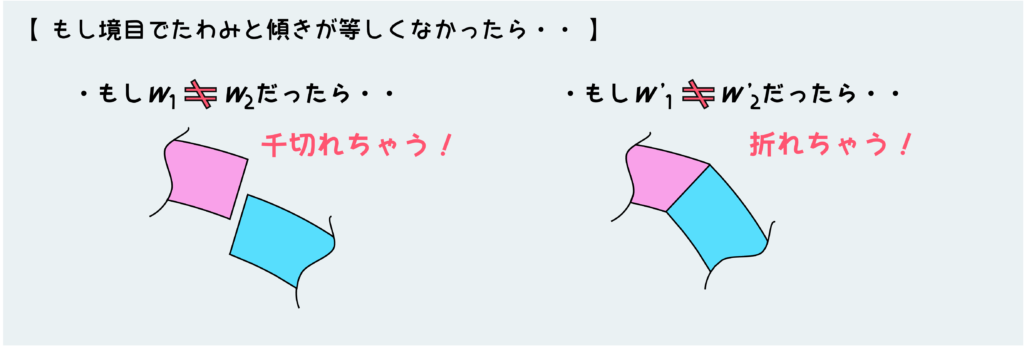
境目の点において、たわみと傾きが等しいという条件を利用すると、区間1と2の微分方程式を使ってさらに2つの条件式を作ることができるので、残り2つの積分定数も決定することができる訳だ。
まとめ
長々と丁寧に書いてきたが、曲げの微分方程式を解く上で重要なことは1つしかない。境界条件を正しく設定することだ。
境界条件の設定の仕方も限られているので、いくつかのパターンを理解すれば何も難しくないと思う。ぜひマスターしてほしい。
- 手順は以下の通りで、最も大事なことは境界条件を正しく見極めること。
- まずは、BMDのときと同じように、はり中に伝わる曲げモーメントを位置xの関数として表現すること。
- 1つの曲げモーメントにつき1つの微分方程式を作り、これを2回積分して、積分定数が2つ出てくる。
- 境界条件を元に積分定数を決定する。
- 境界条件は支点の位置で設定する。場合分けがあるときは、場合分けの境目でもはりがつながっていることを利用して設定する。
理工系人材必読の超おもしろ漫画!!
連載中
『まずは音を出して 音を出さなきゃ音楽は始まらないのよ』
今、忘れかけていた夢への一歩を踏み出す!
いつの間にか多くの人は昔描いた夢のことを忘れてしまう。『宇宙兄弟』は“夢を追うのに遅すぎるなんてことはない”ということを教えてくれます。キャリアや進路に悩むすべての人の背中を押してくれる言葉にあふれている『宇宙兄弟』は多くの社会人や大学生から大絶賛されています。
宇宙開発や飛行士の活動をリアルに描く本作は、理工系の人の知的好奇心を刺激し、未知の問題へ向き合う姿勢を学べる必読書と言っても決して過言ではありません!
ebookjapanなら3巻まで無料で読めるので、気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも!