さて今年の節分はいつも（ここ数十年は２月３日）と違い２月２日だった訳ですが、なんと節分が２月２日になるのは1897年以来124年振りということで大きな話題となりました。
突然ですが、ここで質問です。次に節分が２月２日になるのは何年後でしょうか？
「今年からは２月２日になるのか？」とか「２月２日になるのはまた100年後ぐらいかな？」みたいに思う人も多いかと思いますが…
大間違いです！！
これには天体の動きと暦の成り立ちが関係しています。
どういうメカニズムで節分は動くのか？季節と暦の関係性は？図を交えながら分かりやすく解説していきたいと思います。
（なお、この記事は国立天文台ホームページを参考に執筆しました。私は専門家ではありませんので、厳密には説明が間違っている（というか不適切な）箇所があるかもしれませんが、大筋では正しいと思います。その旨ご了承ください。）
- 次に節分が２月２日になるのが何年後か分からない
- 宇宙の壮大さにドキドキする！
- 節分がどうして動いたのかメカニズムが知りたい！
- ユリウス・カエサルって聞いたことあるけど誰だっけ？
Contents
『真の1年』と『暦の1年』のズレ
まず１年の長さってどれくらいだろうか？
そりゃ365日でしょ。そりゃそうだ。１月１日から１２月３１日までの365日で１年だよね。これは暦上間違いではありませんが、物理現象としては厳密には間違いです。
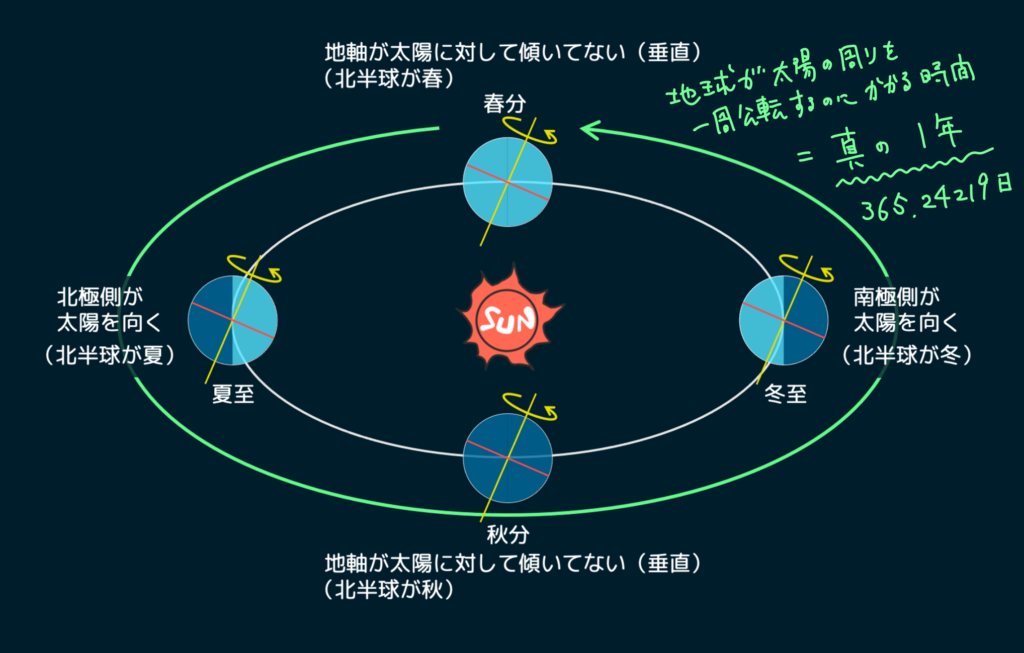
１年というのは天体の動き、つまり太陽の周りを地球が１周する時間で定義されます。地軸が太陽の方を向いている夏至（北半球が夏）から、反対向きの冬至（北半球が冬）を通ってまた夏至に戻ってくるまでが１年です。
この時間は365.24219日であり、ぴったり365日ではないのです。約6時間ほど365日よりも長い時間がかかります。
そうなると、少しずつ暦と実際の季節（天体の動きに基づく四季）がずれてきちゃう訳ですよ。どういうことかと言うと…↓
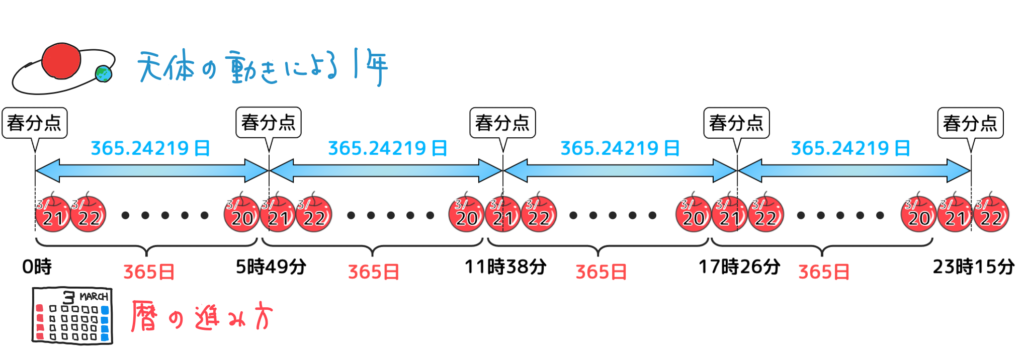
例えばこんな風に、春分になる時刻（地軸が太陽に対して垂直）が時間の経過に伴いどう変わっていくかを考えてみましょう。上の図で、りんご１つが１日です。図の下半分では、りんごが365個並んでいて、これで１年となります。上半分には地球の公転による真の１年の長さを青い矢印で表しています（これはりんご365個分よりも若干長くなっています）。
まず仮のスタート地点としてある年の春分点（春分になる時刻）が３月２１日の０時ぴったり（上図の左端）だとすると、１年経つと「真の１年」と「暦の１年」の差（約６時間分）だけ春分点の時刻がずれます。つまり１年後の春分点は３月２１日の5:49になる。これが積み重なっていくので、４年経つと約１日分ずれてしまい、春分点は３月２１日の23:15になってしまうのです。
「いやまあ１日ぐらいずれたってさ、別にいいんじゃない？」と思うなかれ。《別にいいんじゃない精神》でこれをこのまま進めていくと、400年経つと大雑把に言って”100日”もズレちゃう訳ですよ。これどういう事かって言うと、「もうすぐ桜が咲きそうだなー」という季節に暦を見ると７月頭ごろ、みたいな事になっちゃうってことです。500年ぐらい経つと、「最高気温は35℃を超える猛暑日です」なんてタイミングで暦ではクリスマスが来たりする訳です。
このズレを解消するために、みなさんご存知うるう年（閏年）がある訳ですね。
ご存知の通りうるう年には１日追加されるので、１年が366日になります。さきほど言った通り、４年で約１日のズレが生じていますから、暦に追加の１日が入ることでズレが解消される訳です。
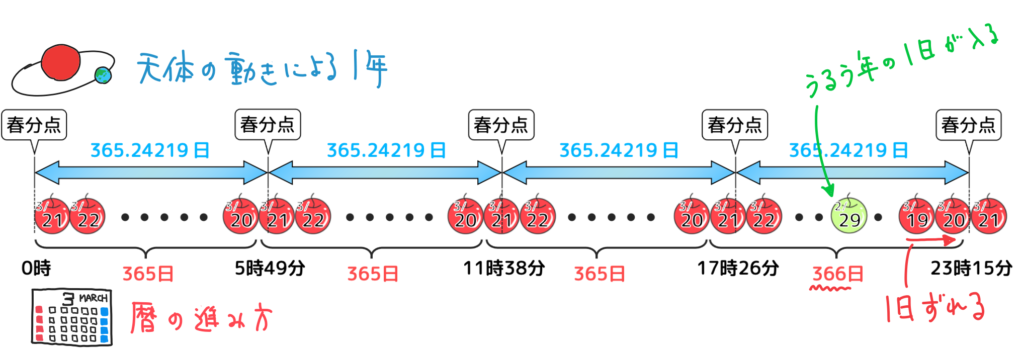
では、うるう年を導入した場合の春分点がどうなるかを考えてみよう。４年後の春分点は、うるう年がなければ３月２１日の23:15な訳ですが、暦が１日増えたことで日付的には１日前の日に動き、３月２０日の23:15になります。これで４年間積み上げてきたズレは、ほぼ解消されています（あとでまた話しますが、ほぼ解消されただけであって完全に解消されていないことを覚えておいてください）。
この４年に１回うるう年を作るシステム、いつ導入されたかというと、古代ローマ時代の紀元前４５年にまで遡るのです。2000年以上前に365日と実際の１年の間のズレに気付いて４年に１回366日にしようって思いつくのすごくないですか？
誰やそんな天才は！？って思いますよね。
導入したのは、古代ローマの英雄ユリウス・カエサル（英語名：ジュリアス・シーザー）です。カエサルは古代ローマを代表する政治家かつ軍人です。「賽は投げられた」「ブルータスお前もか」「来た・見た・勝った」などのカエサルが残した言葉も有名。このカエサルの名を取って、４年に１回うるう年を入れる暦のことをユリウス暦と言います。
カエサルは非常に多才な人物で、軍事だけでなく文筆家としても高く評価されています。彼の人生に触れればきっと大きな刺激を受けることができると思いますので、興味のある方は彼の生涯を記した本を手に取ってみてはいかがでしょうか？
カエサルが導入したユリウス暦（４年に１回うるう年）ですが、さきほどもチラッと言ったように完璧ではありません。つまり１年ごとに春分点となる時刻が後ろに動いていくのですが、うるう年で１日追加されることによって春分点となる時刻が今度は前に動いてしまうのです。その差は約45分。
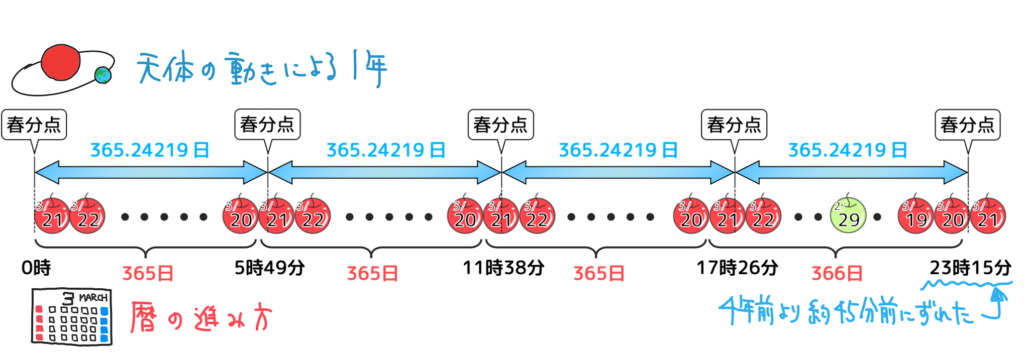
上図のように、最初春分点の時刻が３月２１日０時ぴったりだったものが、４年経ってうるう年が入ると、３月２０日の23:15に動くので、うるう年を導入しても４年で約45分ずつズレていく訳です。どれくらいズレるかと言うと、例えばユリウス歴を2000年続けていくと、ズレは約15日になってしまいます。
という訳で、ユリウス暦のように４年に１回うるう年を入れても少しずつズレが溜まっていきます。そこで、さらなる修正が必要になりました。それが現在私たちが使っているグレゴリオ暦です。
ユリウス暦では４年に１回、なので４００年に１００回うるう年が来ますが、これだと１年ごとに積み上がるズレを修正し過ぎてしまうので、グレゴリオ暦ではうるう年の回数を減らしました。
その回数は、４００年で９７回です。そのためのルールは以下の通り。
- ４の倍数の年はうるう年
- ただし１００の倍数の年はうるう年じゃない
- ただし４００の倍数の年はうるう年
最近で言うと、1700年、1800年、1900年はうるう年じゃないけど、2000年はうるう年で、その他の４の倍数の年は全部うるう年。なので、1601年から2000年までの４００年間の間でうるう年は９７回となる訳です。
これで４００年ベースで見ると、ほとんどズレはなくなりました（もちろん１年で見ると約６時間のズレがあります）。
どうして節分は動いちゃうのか？
さて、ようやく節分の話に入りたいのですが、節分ってそもそもどう定義されるのでしょうか？節分がどうやって決まるのか理解するには、二十四節気というものを知る必要があります。
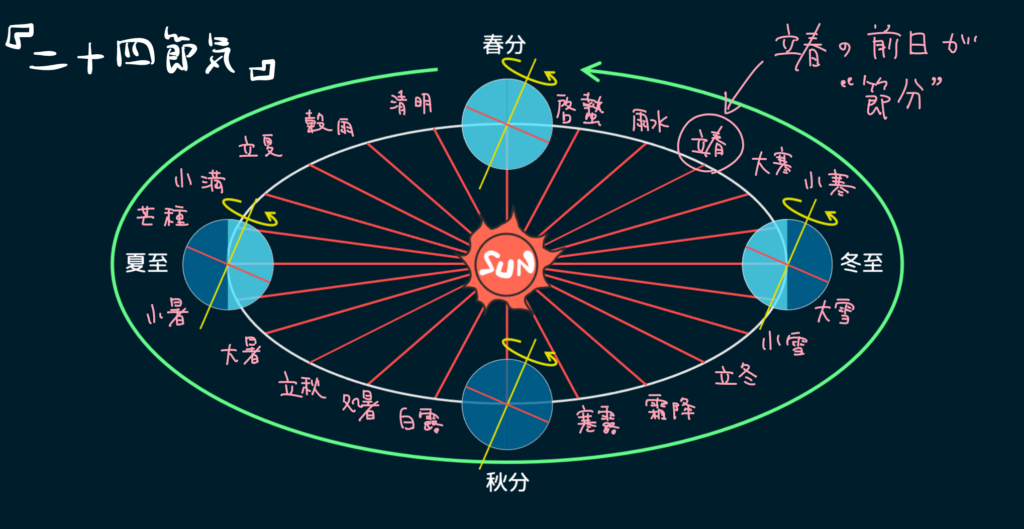
二十四節気というのは１年を２４等分したもので、それぞれの節目に季節に合った名前が付いています。春分・夏至・秋分・冬至もその１つですね。そして立春・立夏・立秋・立冬もよく耳にすると思いますが、これらはそれぞれ春分・夏至・秋分・冬至の中間地点を表しています。
で、現代の節分とはつまり立春の前日のことを言うんですね。
上で説明したように、春分点（ぴったり春分になる時刻）が年を追うごとにズレていきますよね。二十四節気は春分点を基準にして何月何日の何時何分と決まりますから、立春となる時刻も春分点と同じように少しずつ動いていきます。てことは・・節分も立春と一緒に動くってことですね。
では、ここ数十年の立春となった時刻の変化を見て、立春および節分がどう動いてきたか＆今後どう動いていくかを考えてみましょう。
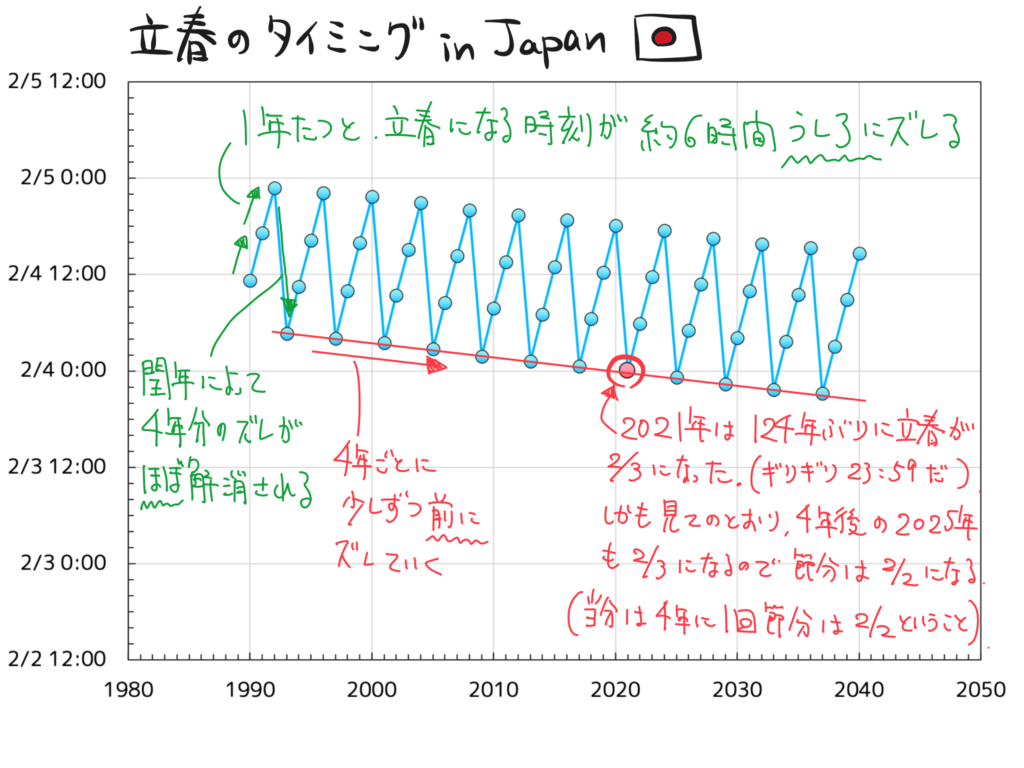
このグラフは、立春となる時刻が年を追うごとにどう動いていくかを示しています。１年経つごとに立春となる時刻は約６時間ずつ後ろにズレていきます。そして４年経つと、このズレをうるう年で巻き戻しますので今度は前に動くのですが、少し巻き戻しすぎるので、４年前と比べて少しだけ前にズレます。この４年周期の動きをずっと繰り返していくのです（４００の倍数以外の１００の倍数の年はうるう年が入らないので、そこの前後だけ８年間後ろにズレ続けます）。
さて細かく立春の動きを見ると、ここ４０年近くは２月４日の中に収まっていたんですが、今年2021年は124年振りに立春が２月３日になったのです。しかもギリギリ２月３日の23:59です。これに伴い、節分は立春の前日なので２月２日になった訳ですね。
さあ冒頭の質問に戻りましょう。次に節分が２月２日になるのは、何年後でしょうか？
答えは４年後の2025年です。
来年（2022年）はまた約６時間後ろにズレるので立春は２月４日、節分は２月３日に戻りますが、その後2024年のうるう年を経て2025年にはまた1日分前にズレてくるので再び立春は２月３日、節分は２月２日になります。
グラフを見てもわかるように、当面は４年に１回節分が２月２日になる年がやってくる訳ですね。
まとめ
最後まで読んでいただき、ありがとうございます。
暦の成り立ちには、太陽を回る地球の動きが密接に関係していたんですね。知っている人にとっては当たり前のことかもしれませんが、意外と知らない人も多いですよね。
普段宇宙のことなんか気にしていないという人も、これを機に少しだけ宇宙に想いを馳せてみるのもいいかもしれません。
