この記事では、主応力および最大せん断応力について解説したい。
主応力の求め方（公式）から、絶対に押さえておくべき特徴まで分かりやすく解説しているので、ぜひ最後まで読んでほしい。
主応力というのは端的に言えば、「最大の垂直応力」および「最小の垂直応力」のことだ。材料中の位置が変われば応力はもちろん変わり、どこかで最大値や最小値が現れるが、ここで言う最大とか最小というのはそういう意味の話ではない。
ある同一の位置でも、想定する面の向きが変わればそこに作用する応力の状態も変わる訳だ。主応力とか最大せん断応力というのは、そういう見る向きが変わったときに変化する応力の中で最大・最小の応力のことを言っている。
このことがよく分かっていないと、主応力についても本質を誤解してしまう可能性があるので、この辺りのことがよく分からない人は以下の記事を先に読んでみてほしい。
応力の２次元座標変換の公式の使い方・何のために使うのか徹底解説！【材力Vol. 5-1】
ひずみの２次元座標変換！公式の使い方・使い所など分かりやすく解説！【材力Vol. 5-2】
- 同じ位置でも、対象とする面の方向が変わるとそこに働く応力は変化する。
- 主応力はある位置において、面を回転させることで変化する垂直応力の中で最大あるいは最小の応力。
- 最大せん断応力は、同じく変化するせん断応力の中で最大のもの。
- 主応力の方向を意味する主軸同士（最大主応力と最小主応力の方向）は直行する。
- 主応力が発生する面には絶対にせん断応力が発生しない。→ つまり、せん断応力が働かない面に発生している垂直応力が主応力
- 最大せん断応力は主軸と主軸のちょうど中間の面に発生する。
溢れでる涙を抑えられない！！
全11巻完結
『君は かけがえのない春の中にいる』
胸の奥底から湧き上がる涙を抑えられない、そんな表現がぴったりな至極の青春漫画
ピアノの旋律、揺れ動く感情、一度しかない14歳の青春を天才・新川直司が描いた傑作です。
突然現れた自由奔放なヴァイオリニスト・宮園かをりに振り回されながらも自身のトラウマと向き合い、再びステージにたつ有馬公正。彼らの甘酸っぱく切ない青春ストーリーは、誰もが経験したことのある14歳の春を思い出させます。これはもう、感動系の漫画として文句なしにオススメできる作品です。アニメ化そして実写映画化もされています。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
Contents
主応力とは？
応力というのは、垂直応力にしてもせん断応力にしても『ある面に対して働いている負荷の大きさ』で定義されるものなので、仮に材料内の同じ位置を見ていたとしても面の向きが変わると作用する応力の種類や大きさは変わることになる。
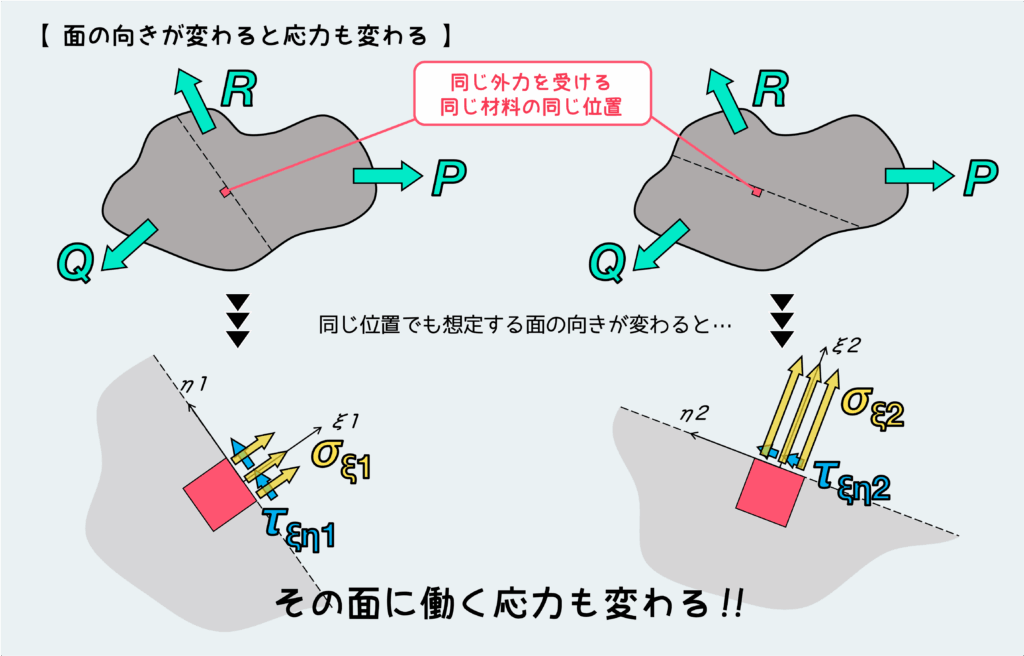
材料内のある位置において、対象とする面の方向を少しずつ変えていくと、そこに働く垂直応力も少しずつ変化するが、その中で最大のものと最小のものを主応力と言う。最大垂直応力を第一主応力と言ってσ1で表し、最小垂直応力を第二主応力と言ってσ2で表す。単に主応力という場合は、第一主応力σ1のことを指している場合が多い。
材料に対して複雑な負荷が作用する場合には、この主応力を把握することが極めて重要になってくる。いわゆるx-y座標系で見た垂直応力がその材料の許容応力を超えていなくても、それを超える主応力が存在すれば破壊に至る可能性はある訳だから、『主応力が許容値を超えないかどうか？』ということを考えることが重要な訳だ。
せん断応力も垂直応力と同じく、想定する面の方向を変えていくと、そこに働くせん断応力の大きさが変化していく。最大せん断応力とは，文字通り「変化するせん断応力の中で最大のもの」を指す。
材料によっては、垂直応力よりもせん断応力に対して弱いものもあり、このような材料の場合は、上記の主応力を考慮するよりもむしろ最大せん断応力に注意を向けることが重要になる。
以下では、これら『主応力』と『最大せん断応力』の具体的な求め方について、公式を紹介して解説していきたい。
主応力・最大せん断応力の求め方
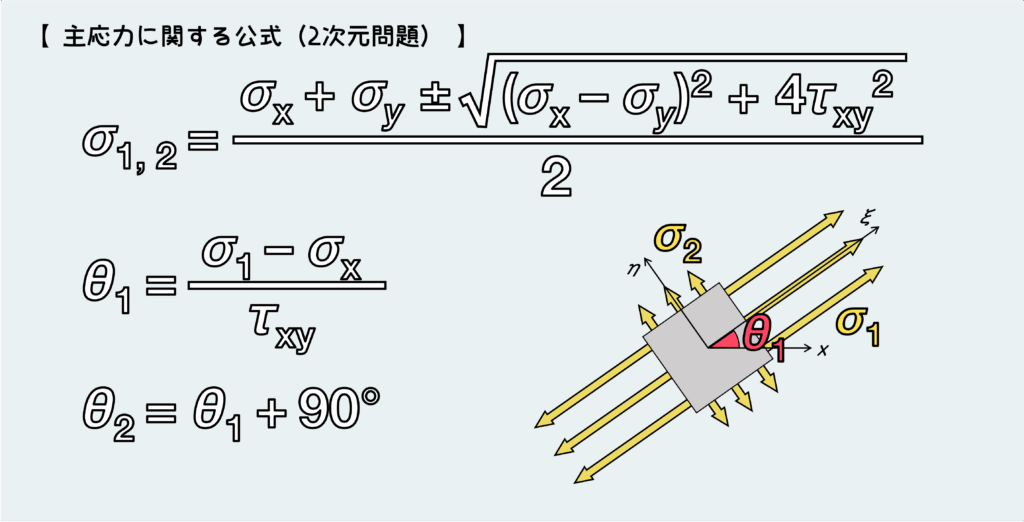
二次元問題における主応力を求める式を下にまとめる。
式の表現はいくつかあるが、この記事ではぼくが個人的に使いやすい形のものを紹介することにする。
主応力の式に±（プラスマイナス）があるが、プラスの方を使うと第一主応力σ1が、マイナスの方を使うと第二主応力σ2が求まる。θ1およびθ2はそれぞれ、主応力が働く面の法線方向がx軸からどれだけ傾いているかを表している。
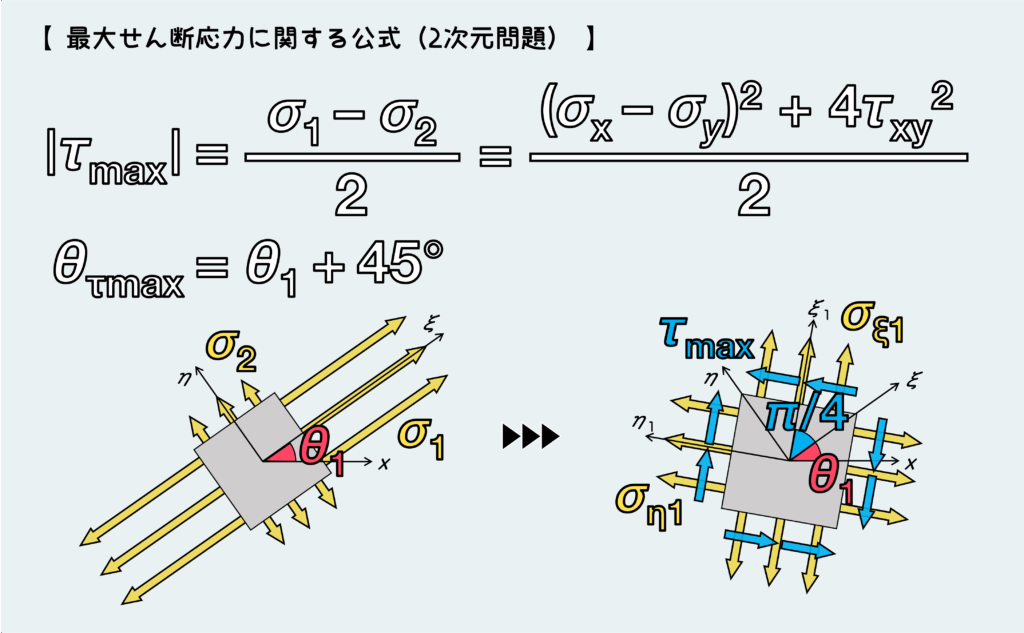
二次元問題における最大せん断応力を求める式を求める式を以下に紹介する。
下図に示す通り、最大せん断応力が働く面は、2つの主応力が発生する面のちょうど中間の向きに発生する。つまり、主軸の向き（θ1）から45°ずれた面に、最大せん断応力が現れるってことだ。
主応力と最大せん断応力の特徴
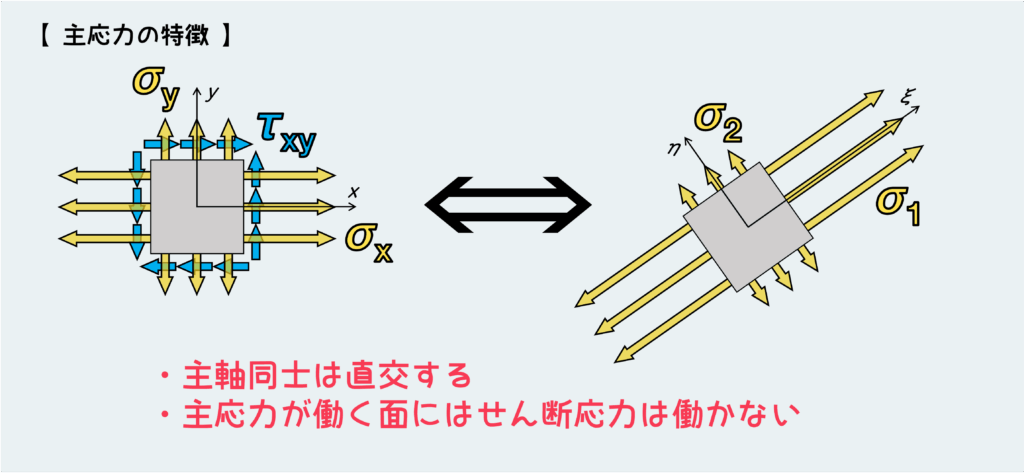
主応力に関する大きな特徴として、第一主応力と第二主応力が発生する面は必ず直交（主軸同士が直交）する。上の公式を見ても分かるが、θ1とθ2の間には必ず90度の差がある。
また、主応力が発生する面には絶対にせん断応力は発生しない。逆に言うと、せん断応力が”0”になるような面に発生している垂直応力が必ず主応力になる。
- 主軸同士は直交する
- 主応力の面にはせん断応力は絶対働かない → せん断応力が働かない面に発生している垂直応力＝主応力
これは超大切な特徴だ。
このことを理解していれば、わざわざ公式を使わなくても主応力を知ることができるケースがある。
最大せん断応力についての大きな特徴は、上述した公式のところでも触れたが、主軸と主軸のちょうど中間の面に発生することである。すなわち、主応力が現れる面から45°傾いた面に最大せん断応力が現れることになる。
また、主応力の面にはせん断応力が働かないことが大きな特徴だったが、最大せん断応力の場合は、必ずしも最大せん断応力が現れる面に垂直応力が発生しないという訳ではない。
多くの場合、最大せん断応力が発生する面には何かしらの垂直応力が同時に発生することになる。
- 主軸から45°傾いた面に最大せん断応力が発生する
- 最大せん断応力の面には、垂直応力が働くことも働かないこともある
唯一、最大せん断応力の面に垂直応力が発生しないようなケースは『純ねじり応力場』と呼ばれるもので、材料にねじりのみが負荷される場合に起こる。このときの主応力はσ1=τmax、σ2= -τmaxとなることが特徴だ。
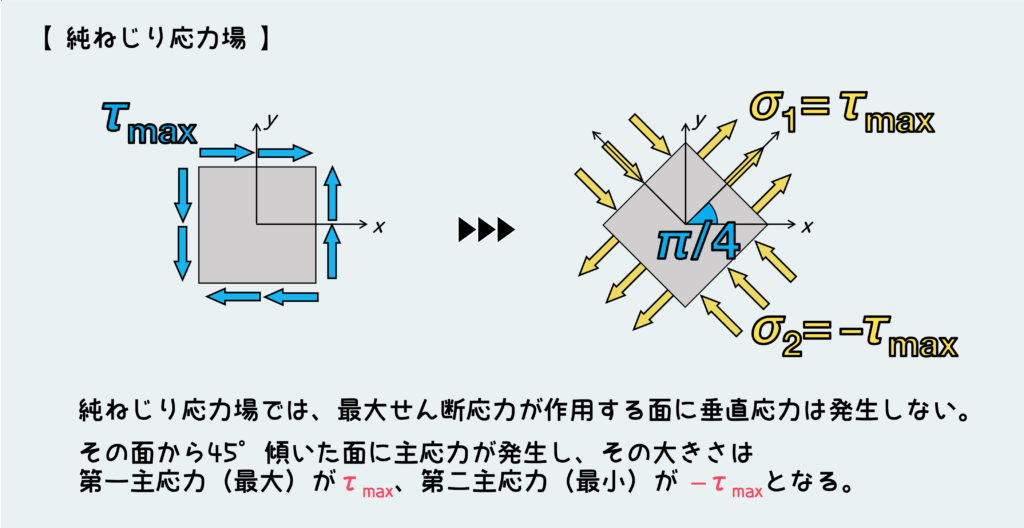
これらの特徴をよく理解していると、上に書いたような公式を使わなくても主応力に関する情報を把握できることもあるので、しっかり押さえておこう。
まとめ
材料が安全かどうかを判断する上で極めて重要な「主応力」と「最大せん断応力」について解説していきたが、ポイントは押さえられただろうか？
応力の座標変換や主応力を考えるツールとして、『モールの応力円』という考え方があるが、これについてはまた別の記事でまとめていきたい。
- 同じ位置でも、対象とする面の方向が変わるとそこに働く応力は変化する。
- 主応力はある位置において、面を回転させることで変化する垂直応力の中で最大あるいは最小の応力。
- 最大せん断応力は、同じく変化するせん断応力の中で最大のもの。
- 主応力の方向を意味する主軸同士（最大主応力と最小主応力の方向）は直行する。
- 主応力が発生する面には絶対にせん断応力が発生しない。→ つまり、せん断応力が働かない面に発生している垂直応力が主応力
- 最大せん断応力は主軸と主軸のちょうど中間の面に発生する。
研究者を志す者 必読！！
全8巻完結
こんなにも知的探究心を刺激される漫画があったとは！
真理のために命をかけた先人たちの物語。
この作品は、現役研究者である私・ぽるこが衝撃を受けた作品として、特に研究者およびこれを志す者には強く本気でオススメします。今ある常識を疑う心、誰に何を言われようと真理を追求する姿勢に触れ、心が動くこと間違いありません。
私自身、世界のトップ研究者だった師匠によく言われた言葉を思い出します。“目の前の現象に楽な答えを持ち出し、疑うことをやめ、真理の追求という困難な道から逃げていないか！？”
本作はこういった研究者の気概なるものを感じる、必読の価値ある一冊です。全8巻ですでに完結していますし比較的手軽に一気読みできます。気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！