前回の記事ではねじりによるせん断応力について説明したが、今回の記事ではねじり変形、すなわちねじれ角に関する問題の解説をしたいと思う。
ねじりの変形問題について苦手意識を持っている人はぜひ最後まで読んでほしい。
読み終わったとき、「何も難しいことなかったな」という感想を持ってもらえると大変うれしく思う。
ねじり問題に関する他の記事は以下を見てほしい。
材料力学 ねじり（トルク）によるせん断応力の考え方【材力Vol. 4-2】
材料力学 ねじりの不静定問題の考え方・２つの例題の超わかりやすい解説【材力Vol. 4-4】
- ねじり変形はねじれ角（面の回転）として現れる。
- ねじれ角の公式は引張変形の伸びの公式と同様な形をとり、ヤング率Eと横弾性係数G、断面席Aと極断面二次モーメントIPが対応している。
- シンプルなパーツ（両端にトルクを受ける部材）に分解し、各部材に伝わる内力（トルク）を決定し、これを元に各部材個別の変形量（ねじれ角）を計算する。各部材のねじれの方向に注意して合算し、構造全体の変形を把握する。
理工系人材必読の超おもしろ漫画！！
連載中
『まずは音を出して 音を出さなきゃ音楽は始まらないのよ』
今、忘れかけていた夢への一歩を踏み出す！
いつの間にか多くの人は昔描いた夢のことを忘れてしまう。『宇宙兄弟』は“夢を追うのに遅すぎるなんてことはない”ということを教えてくれます。キャリアや進路に悩むすべての人の背中を押してくれる言葉にあふれている『宇宙兄弟』は多くの社会人や大学生から大絶賛されています。
宇宙開発や飛行士の活動をリアルに描く本作は、理工系の人の知的好奇心を刺激し、未知の問題へ向き合う姿勢を学べる必読書と言っても決して過言ではありません！
ebookjapanなら3巻まで無料で読めるので、気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
Contents
ねじりを受ける材料の変形
ねじり変形とはどういうものか？
引張・圧縮とは違いなかなかイメージしにくいかもしれない。なぜなら目に見える変形をしない（形状の変化として図に描けない）からだ。
そんな人は『雑巾絞り』を思い浮かべてほしい。雑巾絞りをしたことない人なんていないだろう。
雑巾絞りのような負荷が“ねじり”だ。分かりやすいように色を付けているが、こういう変形をするというのを常に頭に入れておいてほしい。
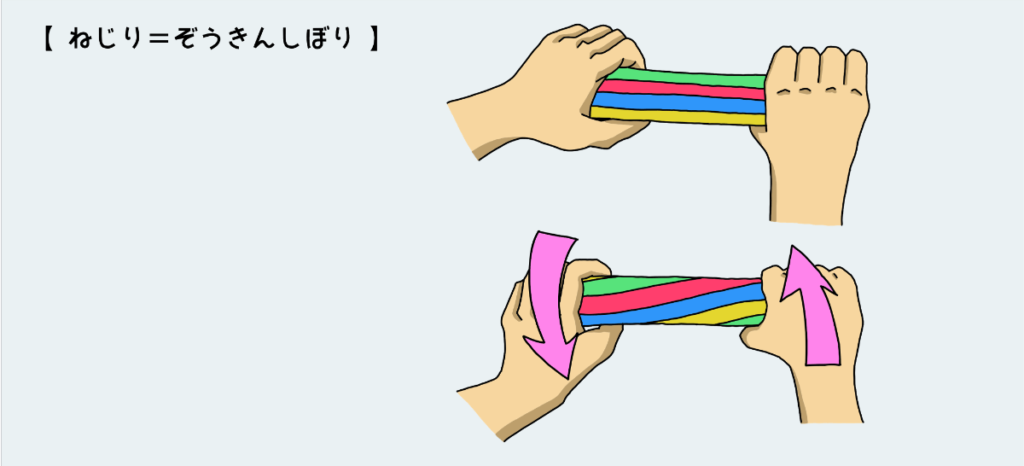
さて、この雑巾絞りを頭に入れた上で、もう少し詳しく見ていこう。
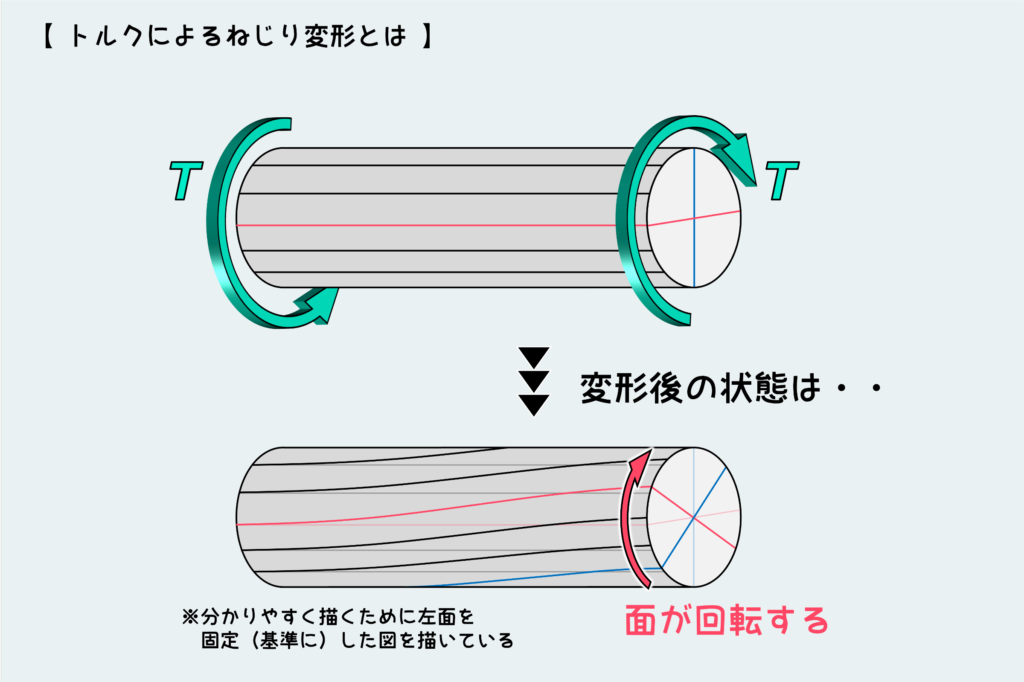
棒の表面に描いた線がどのように動くかに着目し、どのような変形が起きているかを理解しよう。
下の図で描いている通り、ねじり変形で起きる変化は『面が回転する』ことである。
（このように線を描いておかないと変形がぜんぜん見えない。そこが引張・圧縮との違いだ。）
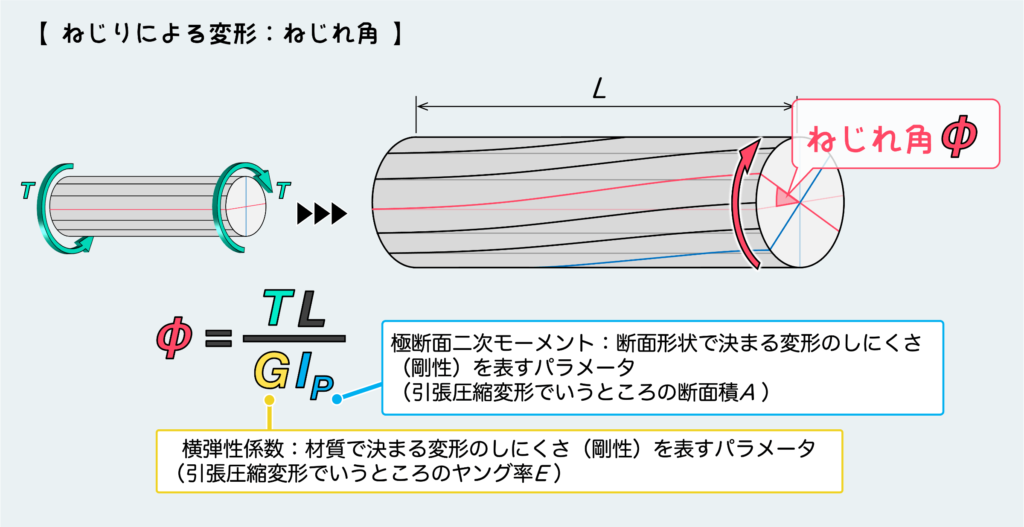
ねじりを受ける材料の変形量は、このように面の回転角として定義され、ねじれ角φ（ファイ）という。
下図のように、左の断面を固定（基準に）して絵を描くと、右端の断面がどれだけ回転したかがねじれ角φである。（下図内で変形前の赤線と変形後の赤線がなす角度）
このねじれ角は下図のような公式で計算することができるが、特別複雑な形をしている訳ではないので暗記してしまう方がいいだろう。後述するが、引張変形の公式と似ていることから、大した労力なく覚えてしまえると思う。
さて、ねじりによる変形量・ねじれ角を計算するための公式を紹介したが、「また公式覚えるの大変だな」と思っている人もいるかもしれない。
しかし、ここで伝えたいことは一つだけだ。
「恐るるに足らぬ！」
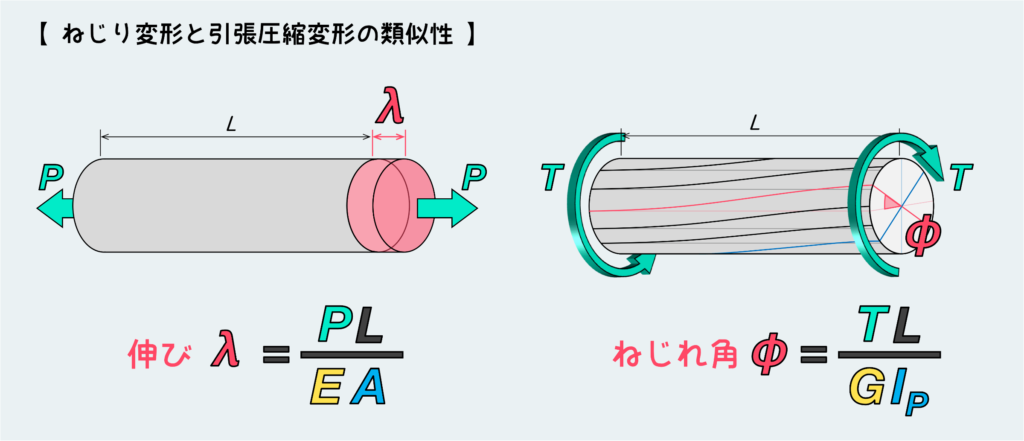
なぜなら、よくよく見ると引張圧縮変形における伸びの公式と非常によく似た形をしているのだ。
下の絵で比較をしている通り、分子は作用している負荷の大きさ（P、T）と部材の長さ（Lで共通）の積であり、分母は剛性（ヤング率E、横弾性係数G）と断面形状パラメータ（断面積A、極断面二次モーメントIP）の積である。
それぞれ同じ性質のもので公式が形成されており、引張圧縮の変形量の公式さえ覚えておけば、新たにねじれ角の公式を覚える必要はないってことだ。
ねじれ角の公式は引張変形（伸び）の公式ととっても似ているので楽に覚えられる！
ここで蛇足的説明を少し加えておきたい。
これらの公式の中で分母側に位置するもの（EAとGIP）はそれぞれ引張剛性およびねじり剛性と呼ばれるもので、いずれも変形のしにくさを表すものだ。剛性は『材質によって決まる剛性』と『断面形状によって決まる剛性』の掛け合わせで決まる。
ヤング率Eや横弾性係数Gは材料の種類によって決まっている物理量で、たとえば普通の鉄鋼材料ならE=206 GPa、G=79 GPaだ。これがたとえばゴムみたいな材料だと、金属なんかよりももちろん変形しにくい材料なので、ヤング率や横弾性係数は金属と比べてはるかに小さな値になる。
また、変形のしにくさは材質だけでなくもちろん断面形状にも影響を受ける。
引張圧縮の場合は、変形量は形状には関係なく断面積Aだけで決まる訳だが、ねじり変形の場合はそう単純ではないので断面積Aの代わりに極断面二次モーメントを使う訳だ。
ねじり変形の超初歩問題
では下のような簡単な例題を通して、ねじり変形の基礎的な考え方をよく理解しよう。
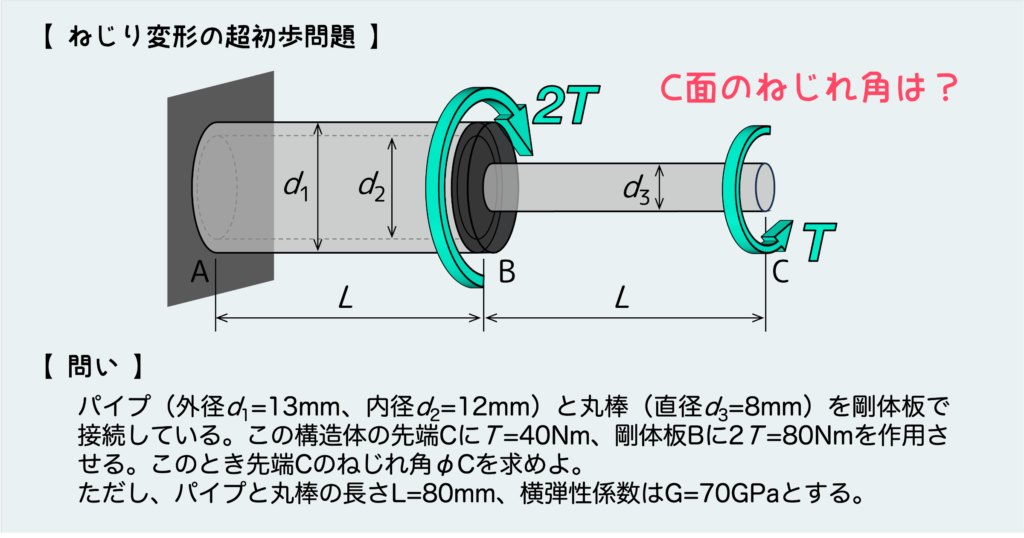
上のような問題の場合、どんなに問題が複雑だとしても初めにやるべきことはいつも決まっている。
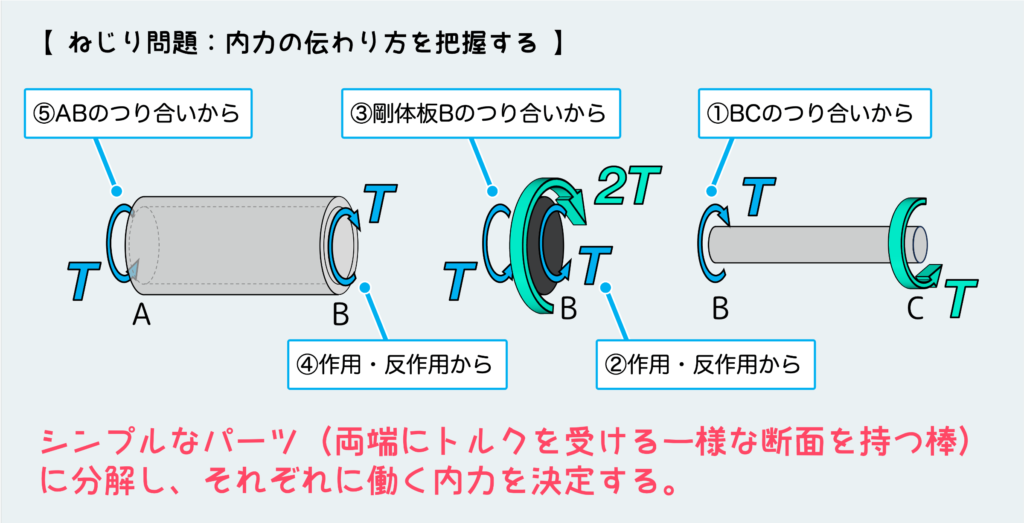
まずは一つのかたまりとして考えられるようなシンプルなパーツに分解して、それぞれに働く内力を決定することである。
分解するポイントは、断面形状が変わる点だったり外力が加わっているポイントだったり、あるいは材質が変わる点だったり、そういう何かしら変化が起きるような点だ。
そういう点で分解して『平衡条件』と『作用・反作用の法則』を駆使して各部材に働く内力を求めることで、複雑な問題をシンプルな問題の組合せにできる訳だ。ここで言うシンプルな問題というのは、公式をそのまま使えるような両端にトルクを受ける一様な断面を持つ棒のことである。
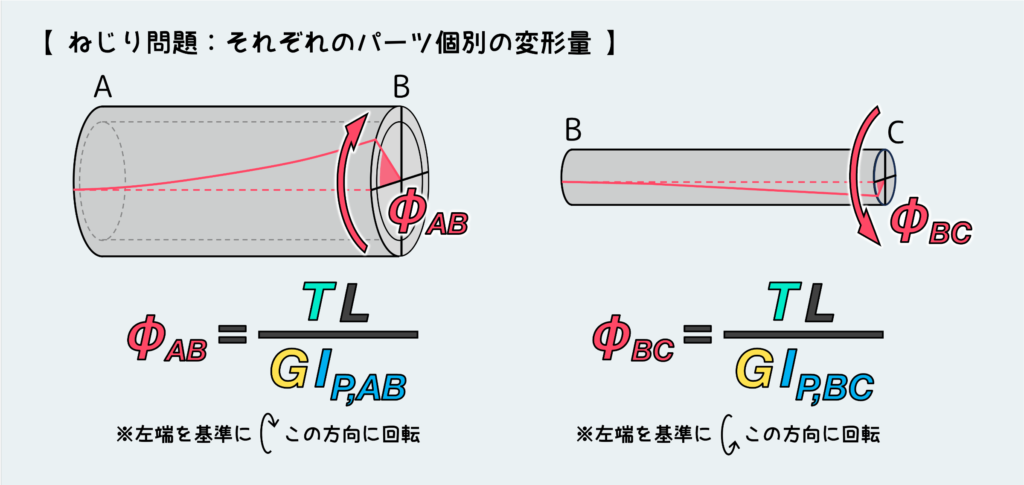
シンプルなパーツに分解することができたら、公式を使って、各パーツ個別の変形量を計算しよう。
ねじり変形の場合は、引張圧縮と違って眼に見える変形をしないので、図に描くときには下図のように部材上に引いた線（変形前：点線、変形後：実線）によって表現することにする。
何度も指摘していることだが、面倒くさがらずにこのような図を丁寧に描くことが材力の理解への近道だ。
ということで下図では分解したパーツABとBCの変形を表現しているが、どちらも左端を仮想的に固定した状態の絵となっている。変形の向きについては、各断面に働くトルクの向きによく注意を払ってほしい。
ここまで出来たらあとは具体的に計算するだけだ。
公式に与えられた情報をぶち込んでいこう。ただし、ここで注意したいのは単位の扱いについてである。公式を扱うときの単位に関する注意点については以下の記事をぜひ読んでもらいたい。
材料力学 公式を正しく使い、計算ミスを減らすコツ【材力 Vol. 0.3】
ここでもう一つ重要なことを伝えたい。公式で得られるねじれ角の単位は『rad：ラジアン』であり『°：度』ではない、ということだ。
なので、『°：度』で答えが知りたければラジアンからの変換が必要だ。
さて、個別のシンプルな部材の変形量について求めることができたら、最後にこれを合算して、この構造全体の変形について考えよう。
一番左のA面は壁に固定されており、B面はAB部分のねじれ角φABだけ回転することになる。さらにここに接続している剛体板は変形しないので、そのままこの回転量を右側の部材BCに伝えることになる。
そしてBC部分は、このφABだけ回転したところをスタート地点として、逆向きにφBCだけ回転することになる。
このような状態を分かりやすく絵に描くと下のようになる。
したがって、求めるべきC面の回転角φCはφBCからφABを差し引いたものになる。（向きは右遠方から見たときに反時計回り方向）
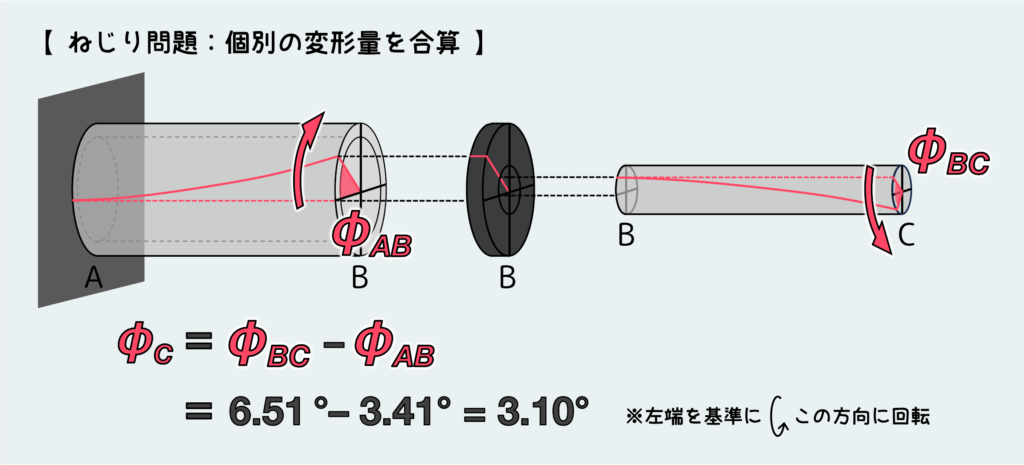
変形の様子を図に描きにくいので、引張圧縮の問題に比べてややこしく感じるかもしれないが、問題の考え方や解き方は引張圧縮問題と全く同じである。公式やこれに必要な量が異なるだけだ。
まとめ
ねじり問題の変形について、超基本的な考え方をまとめたが理解できただろうか。
途中でも触れたが、ねじり問題は、特に変形に関しては引張圧縮問題といろんな点で類似性を持っている。イメージがしにくい、図に描きにくいがためにややこしく感じることはあるかもしれないが、今回解説したことを押さえていくつかの問題を解けば決して難しくないことに気が付くはずだ。
最後にもう一度、この言葉でこの記事の締めとしたい。
「恐るるに足らぬ！」
次はねじりの不静定問題についての解説をしたいと思っているので、ぜひそちらも合わせて覗いてみてほしい。（記事執筆中）
- ねじり変形はねじれ角（面の回転）として現れる。
- ねじれ角の公式は引張変形の伸びの公式と同様な形をとり、ヤング率Eと横弾性係数G、断面席Aと極断面二次モーメントIPが対応している。
- シンプルなパーツ（両端にトルクを受ける部材）に分解し、各部材に伝わる内力（トルク）を決定し、これを元に各部材個別の変形量（ねじれ角）を計算する。各部材のねじれの方向に注意して合算し、構造全体の変形を把握する。
研究者を志す者 必読！！
全8巻完結
こんなにも知的探究心を刺激される漫画があったとは！
真理のために命をかけた先人たちの物語。
この作品は、現役研究者である私・ぽるこが衝撃を受けた作品として、特に研究者およびこれを志す者には強く本気でオススメします。今ある常識を疑う心、誰に何を言われようと真理を追求する姿勢に触れ、心が動くこと間違いありません。
私自身、世界のトップ研究者だった師匠によく言われた言葉を思い出します。“目の前の現象に楽な答えを持ち出し、疑うことをやめ、真理の追求という困難な道から逃げていないか！？”
本作はこういった研究者の気概なるものを感じる、必読の価値ある一冊です。全8巻ですでに完結していますし比較的手軽に一気読みできます。気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！