公式ってうまく使えているだろうか？実は公式こそ答えが合わない原因かもしれない。
理工系の人間にとって公式というものはとっても頼りになる武器だ。多くの学生は、毎日のように何かしらの公式を使っていることだと思う。
でもこんな人も中にはいるんじゃないだろうか？
適切な公式を使っているし、計算間違いはしていないはずなのに答えが合わない…
そういう人は公式を使うときに単位を気にしていないのかもしれない。公式はとっても便利なものだけど、正しく使えないと正しい答えには導いてくれない。ということで、今回は公式を使うときの単位の扱い方について説明したい。特に、「材料力学の公式に数値を代入するときのコツ」は計算ミスを連発している学生なんかには必見の内容なので、ぜひチェックしてほしい。
- 問題で与えられた数値を（何も考えずに）公式につっこんではダメ！
- 公式に入れる数値の単位によって、出てくる答えの単位が変わる。
- 数式の中に単位を書き入れていくと間違いが減る！
- 以下のように単位変換してから代入するのがオススメ！
- 力（荷重）：（N）（ニュートン）
- 長さや面積：（mm）や（mm2）
- 応力・ヤング率：（MPa）
Contents
単位に注意せずに公式を使うとどうなる？
前２回の記事（材料力学 （kgf）から（N）への変換など単位のキホンその１【材力 Vol. 0.1】、材料力学 応力の単位（MPa）など単位のキホンその２【材力 Vol. 0.2】）でも単位の重要性について説明したわけだけど、もちろん公式を使うときも単位に注意するのはとても大切なことだ。これに関しては簡単な公式で具体例を挙げながら説明した方がわかりやすいだろう。
下の絵のような問題を考えてみてほしい。
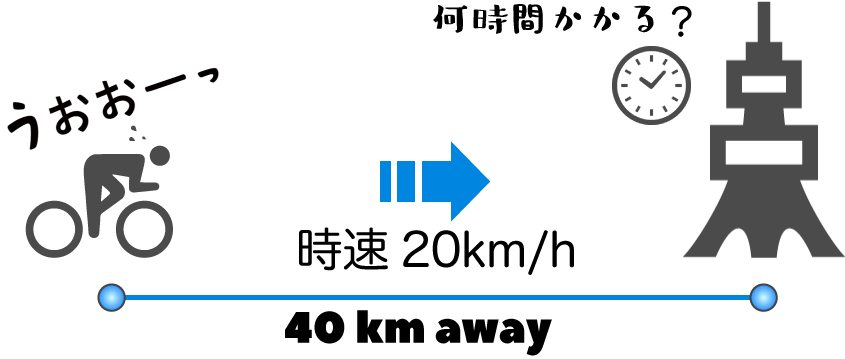
これが解けない人はいないだろう。小学生でも知ってる以下の公式を使えばいい。距離と速度、そして時間の関係を表した公式は、
（かかる時間）＝（距離）÷（速度）
だ。これを使って、上の絵のような問題を解いてみたい。
40 km離れた場所まで時速20 kmで行くわけだから、公式の（距離）に”40”を入れて、（速度）に”20”を入れて…
（かかる時間）＝ 40 ÷ 20 ＝ 2 時間
というわけで答えは２時間となる。これは何も問題ない。では次の例ではどうだろうか？
今君は、時速160 kmの球を投げられるピッチャーを相手にしている。マウンドからホームまでの距離は約18 mあるが、ピッチャーが投球した後いったい何秒後にバットを振ればいいだろう？
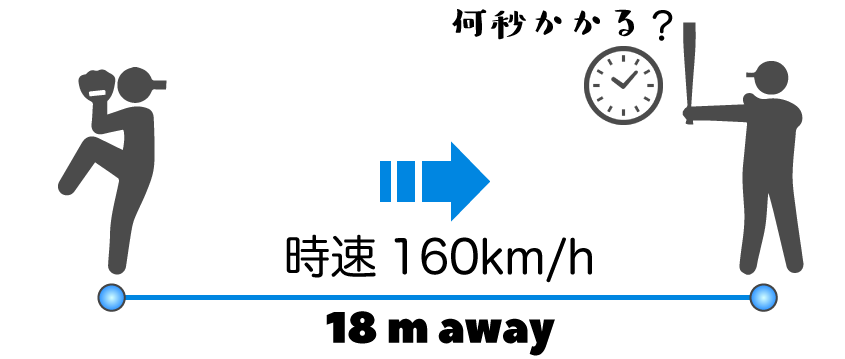
18 m離れた場所まで時速160 kmで行くわけだから、公式の（距離）に”18”を入れて、（速度）に”160”を入れて…\begin{eqnarray}（時間）&=&\frac{（距離）}{（速度）}\\[4pt]
&=&\frac{18}{160}\\[4pt]
&=&0.11\end{eqnarray}（秒）で聞かれてるし、なんかわかんないけど単位は（秒）かな。うん、答えは0.11秒！
というわけで答えは 0.11 秒になる……ってそんなわけない！
距離の18（m）と時速160（km）をそのまま計算してはいけないし、160（km）は時速（つまり160（km/h）なんだからこのまま計算したら出てくる答えは（秒）ではなく（時間）だ。
公式を使って何かを計算するときは、代入する数値の単位を揃えたり、求めたい形に変換しないといけない。
まずは距離に関する単位を（m）に揃えよう。速度の160（km/h）は 160000（m/h）ってことだな。
で、今知りたいのはボールがマウンドに来るまでに何（秒）かかるか？なので、時間に関する単位を（時間 h）から（秒 s）に変換しよう。
てことは、速度160000（m/h）= 160000 ÷ 3600 = 44.4（m/s）になるな。こいつらを公式に代入して…\begin{eqnarray}（時間）&=&\frac{（距離）}{（速度）}\\[4pt]
&=&\frac{18 \ (m)}{44.4 \ (m/s)}\\[4pt]
&=&0.41 \ (s)\end{eqnarray}ということで、答えは0.41秒！
こんな風に計算できればOKだ。上のように、式の中に単位を書き入れて計算するのがオススメだ。そうすると、単位変換忘れや答えの単位を間違うといったくだらないミスをなくすことができる。今回の例では、（m）が分母分子で消し合って、最後に（s）だけが残ることが分かりやすいだろう。
これは簡単な例だったから、こんな間違いするわけないって思うかもしれない。しかし、材料力学の問題になった途端、単位について思考停止してしまうのか、そもそも応力とかの単位が何か分かっていないのか、こういうミスをしている学生は本当に多い。
数式の中に単位を書き入れて計算すると間違いが減る！
くどいかもしれないが、次に材料力学の問題ではどんな間違いが起こるのか見てみたい。例えば、下の絵のようにある負荷が作用した鉄線がどれだけ伸びるか？という問題があったとしよう。
問題自体はどうと言うことはない。なんてったって公式がある。伸びλ は荷重 P 、材料の長さ l 、断面積 A 、ヤング率 E を用いて \(\lambda=\large\frac{Pl}{EA}\)というように求めることができる。しかし、上で説明した野球の例と同じく、単位を気にせず公式を使うとおかしなことになる。
公式は \(\lambda=\large\frac{Pl}{EA}\)だから、荷重P に2000（kgf）を、長さl に1（m）を、ヤング率E に206（GPa）を、断面積A にπ/4×1.52を入れて…\begin{eqnarray}（伸び）\lambda&=&\frac{（力）P（長さ）l}{（ヤング率）E（断面積）A}\\[4pt]
&=&\frac{2000\times1}{206\times\pi/4\times1.5^2}\\[4pt]
&=&5.5\end{eqnarray}単位はたぶん（mm）かな。答えは5.5（mm）だ！
これは言うまでもなく間違っている。問題で与えられた数値を何も考えずに公式に投げ込んだ結果がこの有様だ。
さらに不幸なことに、答えだけを見ると間違っているかどうかを判断することはできない。1（m）の棒に2000（kgf）作用させたときに5.5（mm）伸びると言われたら、まあそんなもんか、と思ってしまう人も多いだろう。つまり、答えを見ても自分の解答がおかしいと気付けないということだ。
上のような計算のやり方は、単位が揃ってなさすぎてハチャメチャである。でも実際、平気でこういう事をしている人は悲しいほどに多いのである。
ではどんな風に計算するのがよいだろうか？
材料力学の公式に数値を代入するときのコツ
もちろん単位を揃えればよい。しかし、ただただ単位を揃えるだけではダメだ。センスがあるとは言えない。単位を揃えるということは、単位変換をする必要があるということだ。いちいち全てに対して闇雲に単位変換をしていたのでは、計算ミスをするリスクを無駄に高めてしまう。ミスするリスクを減らすためには、コツを学ぶ必要がある。
ずばりコツは、長さ系は（mm）、力は（N）、応力やヤング率は（MPa）に統一することだ。理由は以下の２つだ。
- 通常材力で扱う単位が（mm）（N）（MPa）である。そのため、問題で与えられる条件の単位もこれらであることが多く、つまり単位変換する事なく使えるということだ。
- （MPa）=（N/mm2）である。つまり、公式に力や長さの数値を代入するときに（N）と（mm）を使えば、自然と得られる応力の単位が（MPa）になり、場合によってはうまいことヤング率の（MPa）と消しあったりしてくれる。
やはり具体例を見た方が早いだろう。もう一度上でみた丸棒を引っ張る問題を考えてみよう。今回はついでに作用する応力も求めてみたい。
まずは良くない例だ。以下の例は単位の扱いが間違っている訳ではないので、答え自体は正解である。だが、コツを理解していないために無駄に計算が複雑になってしまう。
応力の単位で（Pa = N/m2）が出てくるから、力の単位は（N）に、長さの単位は（m）にしとこうかな。棒の長さは1（m）で、直径は0.015（m）、力は20000（N）、ヤング率206×109（Pa）だな。これを公式に入れて…\begin{eqnarray}（応力）\sigma&=&\frac{（力）P}{（断面積）A}\\[4pt]
&=&\frac{20000 \ (N)}{\pi/4\times0.015^2 \ (m^2)}\\[4pt]
&=&113176848 \ (N/m^2)\\[4pt]
&=&113176848 \ (Pa)\end{eqnarray}で、最後に単位を（MPa）にしたいから、えーと10-6かけて…\begin{eqnarray}（応力）\sigma&=&113176848 \ (Pa)\times10^{-6}\\[4pt]
&=&113 \ (MPa)\\[10pt]
（伸び）\lambda&=&\frac{（力）P（長さ）l}{（ヤング率）E（断面積）A}\\[4pt]
&=&\frac{20000 \ (N)\times1 \ (m)}{206\times10^9 \ (Pa)\times\pi/4\times0.015^2 \ (m^2)}\\[4pt]
&=&0.00055 \ \frac{(N\times{m})}{(Pa\times{m}^2)}\\[4pt]
&=&0.00055 \ (m)\\[4pt]
&=&0.00055 \ (m)\times10^3\\[4pt]
&=&0.55 \ (mm)\end{eqnarray}
次に、コツをしっかり理解している人の解答を見てみよう。かなりシンプルになるはずだ。
単位系は（mm）（N）（MPa）に揃えよう。棒の長さは1000（mm）で、直径は15（mm）、力は20000（N）、ヤング率206000（MPa）だな。これを公式に入れて…\begin{eqnarray}
（応力）\sigma&=&\frac{（力）P}{（断面積）A}\\[4pt]
&=&\frac{20000 \ (N)}{\pi/4\times15^2 \ (mm^2)}\\[4pt]
&=&113 \ (N/mm^2)\\[4pt]
&=&113 \ (MPa)\\[10pt]
（伸び）\lambda&=&\frac{（力）P（長さ）l}{（ヤング率）E（断面積）A}\\[4pt]
&=&\frac{20000 \ (N)\times1000 \ (mm)}{206000 \ (MPa)\times\pi/4\times15^2 \ (mm^2)}\\[4pt]
&=&0.55 \ \frac{(N\times{mm})}{(MPa\times{mm}^2)}\\[4pt]
&=&0.55 \ (mm)\end{eqnarray}
無駄な単位変換をすればするほど、計算はややこしくなり、ミスするリスクが高まる。コツを知っていれば、かなり簡単でシンプルに計算できるはずだ。
この例題はわざと問題の条件で（cm）とかを使っているが、基本的には材力での問題では（mm）が使われている。だから、わざわざ『（mm）を（m）に単位変換して、応力を（Pa）で求めた後に10-6かけて（MPa）にする』みたいなことしなくても、与えられた（mm）と（N）を使って計算すれば自然と求まる応力の単位は（MPa）になる。
長さ系（mm）、力（N）、応力・ヤング率（MPa）を使おう。
（MPa）=（N/mm2）
まとめ
分かっている人にとっては、ものすごく簡単で基本的なことを長々と書いてしまった。しかし、こういう本質的な問題ではないところでミスしている人は意外と多いし、そんな人は一度しっかり今回説明したような内容を見直さないと、材力に限らずすべての理工系科目でずっと間違い続けることになるだろう。
公式は上手に使いこなさないことには、いろいろな問題を解くことはできないので、ぜひ適切に使いこなせるようになってほしい。
- 問題で与えられた数値を（何も考えずに）公式につっこんではダメ！
- 公式に入れる数値の単位によって、出てくる答えの単位が変わる。
- 数式の中に単位を書き入れていくと間違いが減る！
- 以下のように単位変換してから代入するのがオススメ！
- 力（荷重）：（N）（ニュートン）
- 長さや面積：（mm）や（mm2）
- 応力・ヤング率：（MPa）
