断面二次モーメントって一体何なのよ！
あ！あの形状の断面二次モーメントが知りたい！でも教科書がない！
そんな人のために、サクッと色んな形状の断面二次モーメントを3分で解説していきます！
溢れでる涙を抑えられない！！
全11巻完結
『君は かけがえのない春の中にいる』
胸の奥底から湧き上がる涙を抑えられない、そんな表現がぴったりな至極の青春漫画
ピアノの旋律、揺れ動く感情、一度しかない14歳の青春を天才・新川直司が描いた傑作です。
突然現れた自由奔放なヴァイオリニスト・宮園かをりに振り回されながらも自身のトラウマと向き合い、再びステージにたつ有馬公正。彼らの甘酸っぱく切ない青春ストーリーは、誰もが経験したことのある14歳の春を思い出させます。これはもう、感動系の漫画として文句なしにオススメできる作品です。アニメ化そして実写映画化もされています。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
Contents
断面二次モーメントとは？
断面二次モーメントは、『形状』的に材料の曲がりにくさを表現するパラメータです。断面形状の寸法や形状によって変わるパラメータで、大きくなるほど材料が断面形状的に曲がりにくい（同じ負荷でもたわみ量が少ない）ということになります。
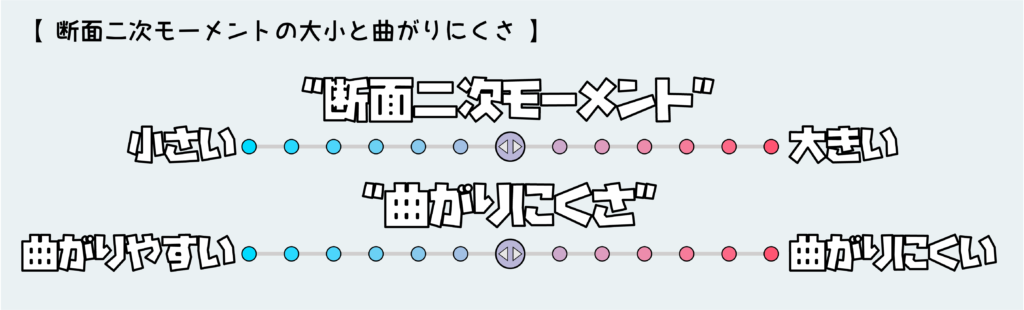
断面二次モーメントは応力や変形量（たわみ量）を計算するときに使います。
重要なのは『断面二次モーメントは断面上のどの軸を基準軸にするかで変わる』ということです。応力にしろ変形量にしろ、その形状の図心を通り、かつ曲げの方向に垂直な方向の軸に関する断面二次モーメントを使う必要があります。
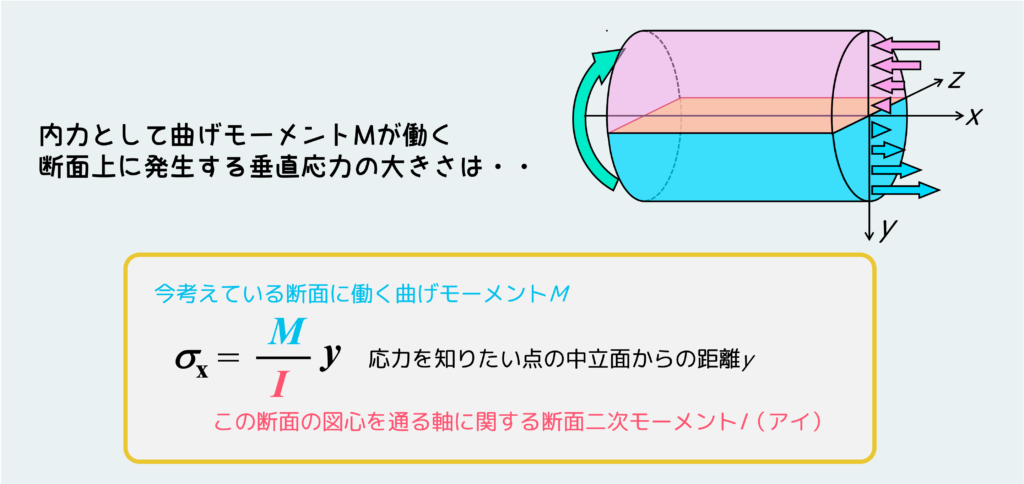
なので、同じ断面形状でも曲げの向きが変わると基準となる軸の向きが変わり、断面二次モーメント自体も変わるし、曲げによる応力の分布の仕方も変わります。
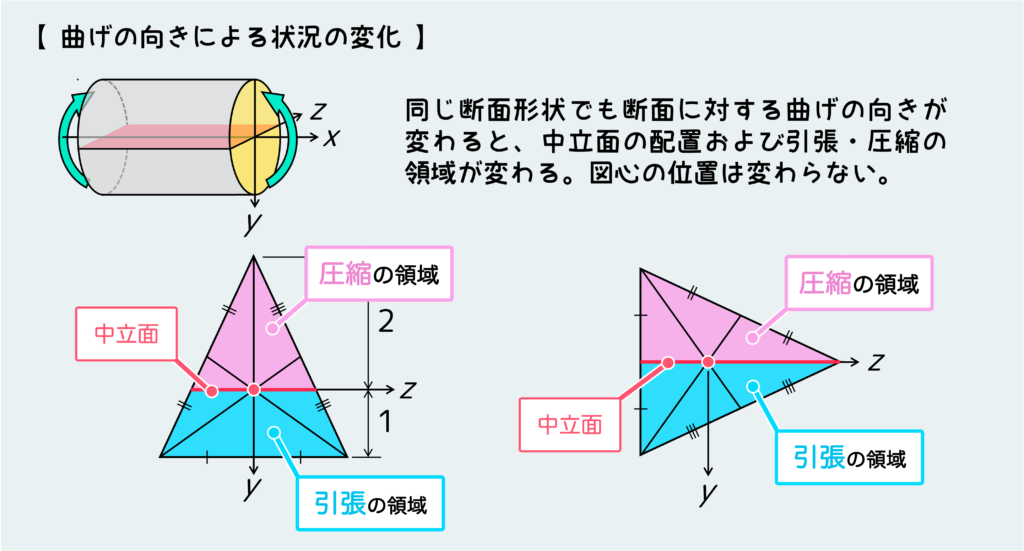
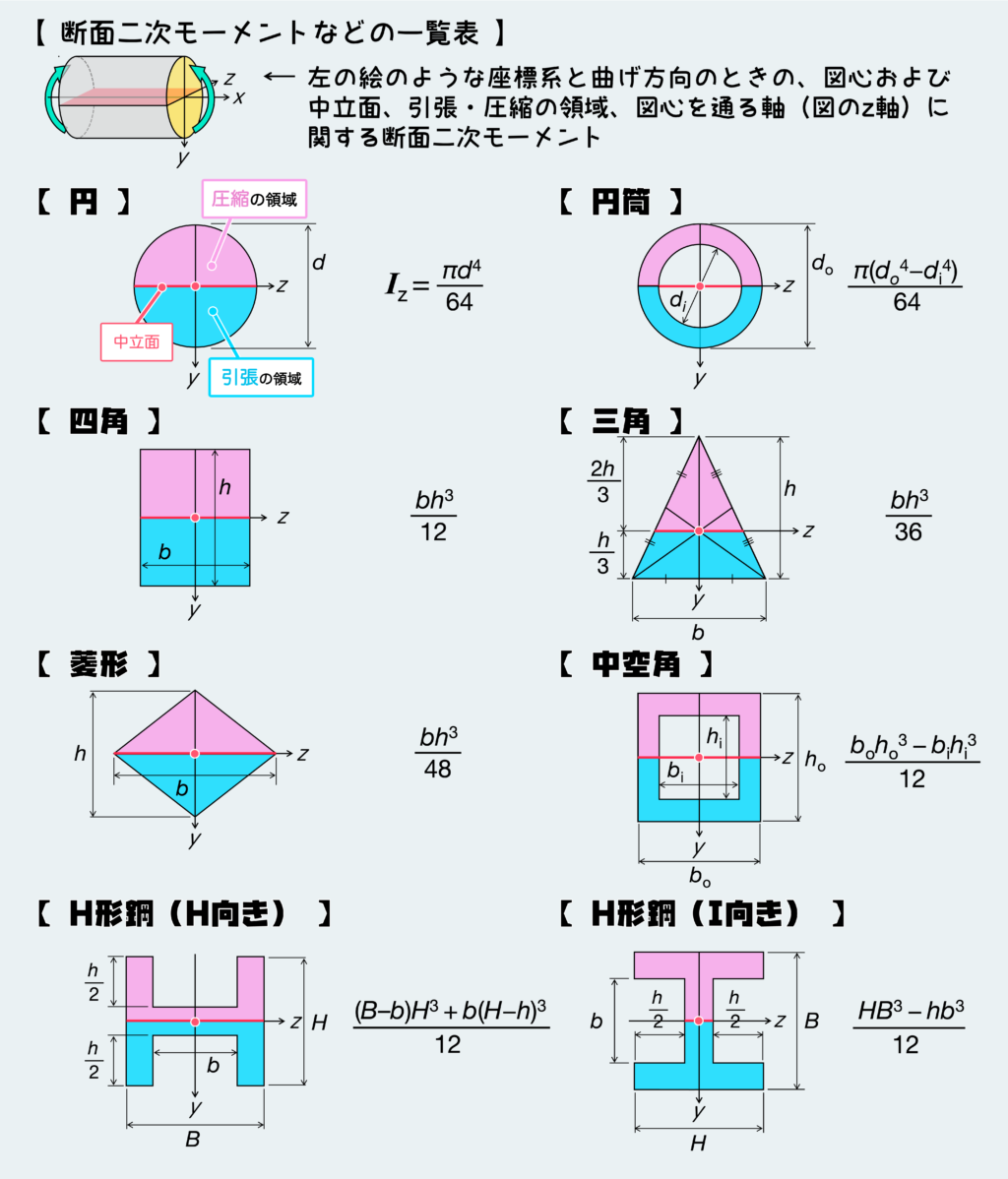
代表的な断面二次モーメントの計算式は下の図の通りです。
これで大抵の形状の断面二次モーメントはカバーされてると思います。
仮にもっと複雑な形状のものが知りたい場合は、定義に基づき頑張って計算するか、もしくは基本形状の組み合わせに分解して計算することになります。
基本形状の組み合わせにして計算する方法の一例は下記の記事を読んでみてください。
曲げモーメントから曲げ応力を計算する方法が絶対分かる記事【材力Vol. 6-6】
関連する記事
さらに詳しく関連する内容について学習したい人は以下の記事を読んでみてください。
溢れでる涙を抑えられない！！
全11巻完結
『君は かけがえのない春の中にいる』
胸の奥底から湧き上がる涙を抑えられない、そんな表現がぴったりな至極の青春漫画
ピアノの旋律、揺れ動く感情、一度しかない14歳の青春を天才・新川直司が描いた傑作です。
突然現れた自由奔放なヴァイオリニスト・宮園かをりに振り回されながらも自身のトラウマと向き合い、再びステージにたつ有馬公正。彼らの甘酸っぱく切ない青春ストーリーは、誰もが経験したことのある14歳の春を思い出させます。これはもう、感動系の漫画として文句なしにオススメできる作品です。アニメ化そして実写映画化もされています。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
