さて今回は『せん断応力』について3分でサッと分かる記事です。
垂直応力とは違ってイメージしにくく、苦手意識を持ってしまう人も多いでしょう。
せん断応力とは何か？垂直応力との違いや求め方など、、気になる人は絶対役に立ちますのでぜひ読んでみてください。
夢へ駆ける少女の姿に感涙！！
12巻連載中
「司先生は…っ わたしが世界一になりたいって言ったら手伝ってくれますか？」
2025年1月アニメ化、そして米津玄師氏が主題歌を逆オファーしたということで話題の本作。
「自分には何もない」と卑下する小さな少女が「金メダルを獲れるスケーターに絶対になりたい！」と夢へ向かって駆け出す。彼女のひたむきで熱い想いに胸を打たれること間違いなしです。
ebookjapanなら2/4までなんと3巻無料で読めてしまいます！まだ全然知らなかったという人にもアニメの放送を待ちきれないという人にもチャンスです！
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
せん断応力とは？
せん断応力とは『ある面に対して、その面に沿うような、面に平行な方向の負荷』のことです。言葉で説明するとよく分からないので、図で見た方がいいでしょう。
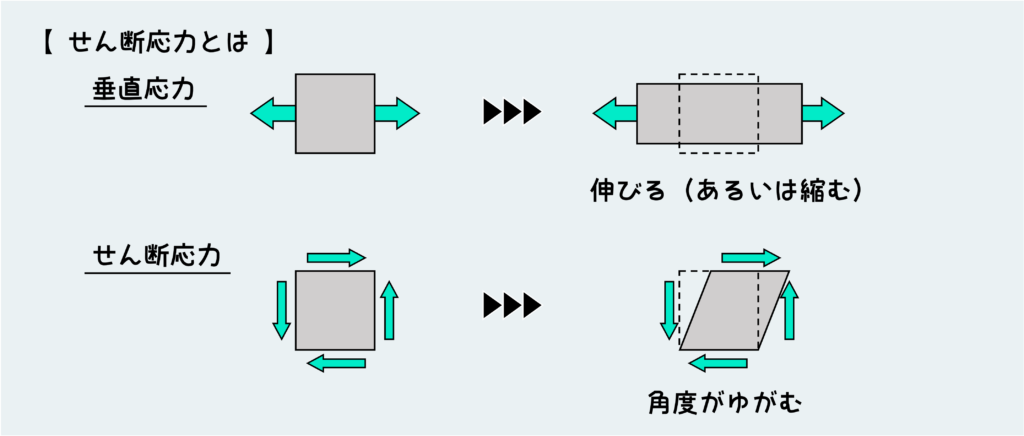
このように、せん断応力は垂直応力と違い、材料を伸び縮みさせるような変形は引き起こさず、角度を歪ませるような働きをします。この角度の歪みをせん断ひずみと言いますが、これについては別の記事で説明したいと思います。
せん断応力を表す記号はギリシャ文字のτ（タウ）で、単位には垂直応力と同じく【Pa】系を使います。材料力学でよく使うのはもちろん【MPa】です。
せん断応力が登場するいくつかのパターンを紹介します。
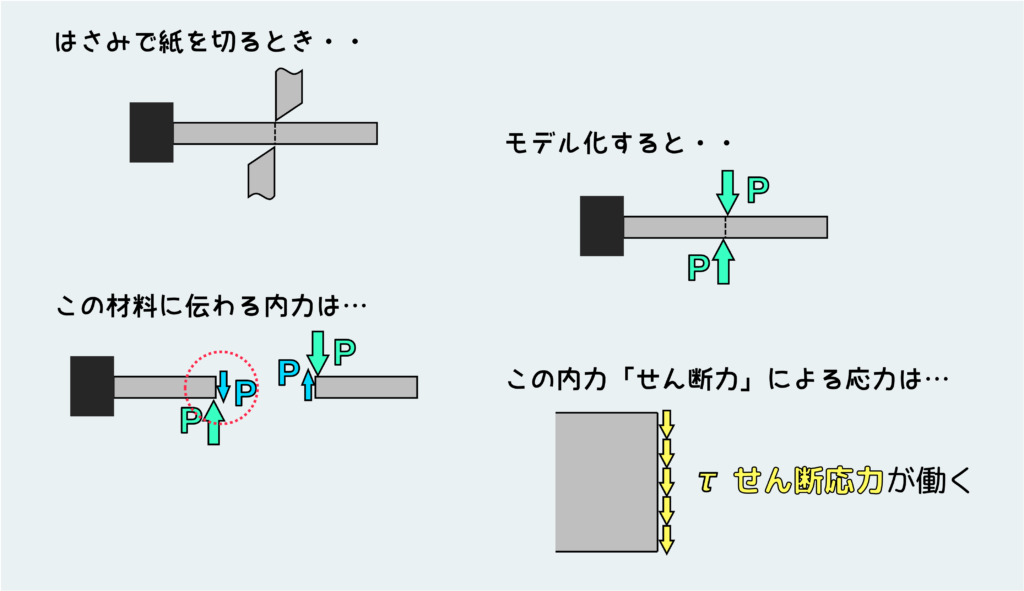
まずは最も身近なシーンとして、はさみで紙を切るシチュエーションです。
はさみで切るとき、この紙の断面には上下からせん断力という面に沿った力が働きます。これによる応力がせん断応力という訳です。
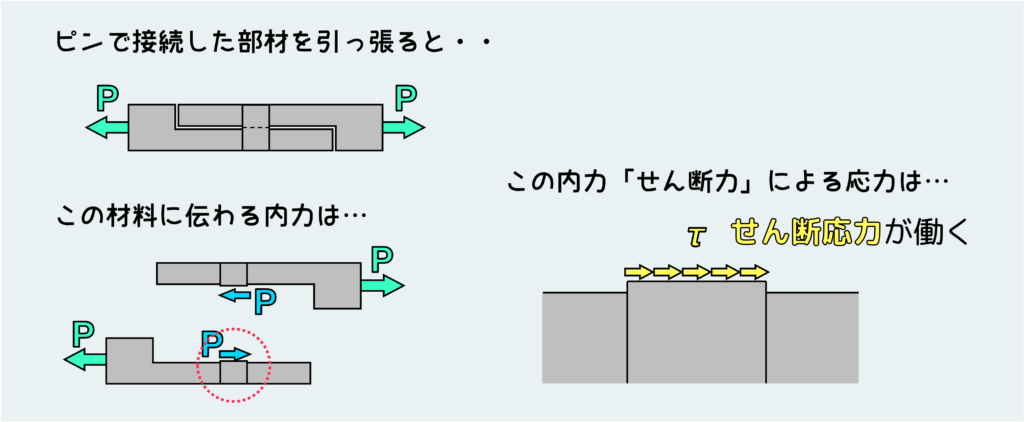
次に、ピンやリベット、ボルトなど工業部品には欠かせない締結部材です。これらの部品の断面にも、下図のようにせん断力が内力として働きます。その結果、この断面にはせん断応力が発生します。
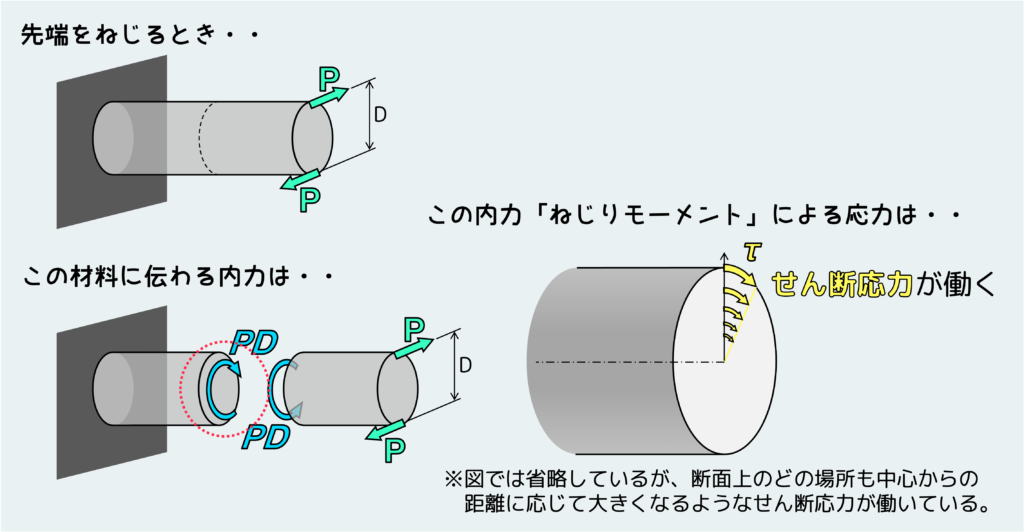
最後に、材料力学において最も代表的なものとして、ねじり問題があります。
ねじりを受ける材料の断面には、先ほどまでの例とは違ってせん断力が働いている訳ではありません。ねじりの場合には、断面上にねじりモーメント（トルク）が働き、これにより上の例とは違って、一様ではない分布をもったせん断応力が働きます。
せん断応力の求め方について、ここではめちゃくちゃ簡単に公式に触れるのみにしておきます。詳細については各テーマを細かく噛み砕いて説明した各記事を読んでみてください。
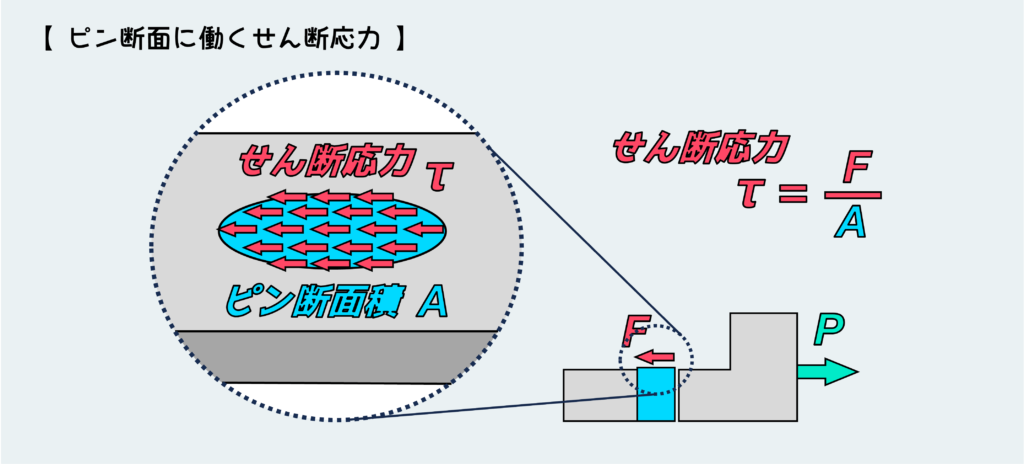
このようなケースでは、断面には一様なせん断応力が発生しているとみなすため、考え方は引張・圧縮問題における垂直応力と同じです。つまり、その断面に働いているせん断力を断面積で割ることでせん断応力が求まります。
下図の例では、ピン断面に働くせん断力Fは外力Pと等しいため、Pを断面積Aで割ることでこのピン断面に発生するせん断応力が求まります。
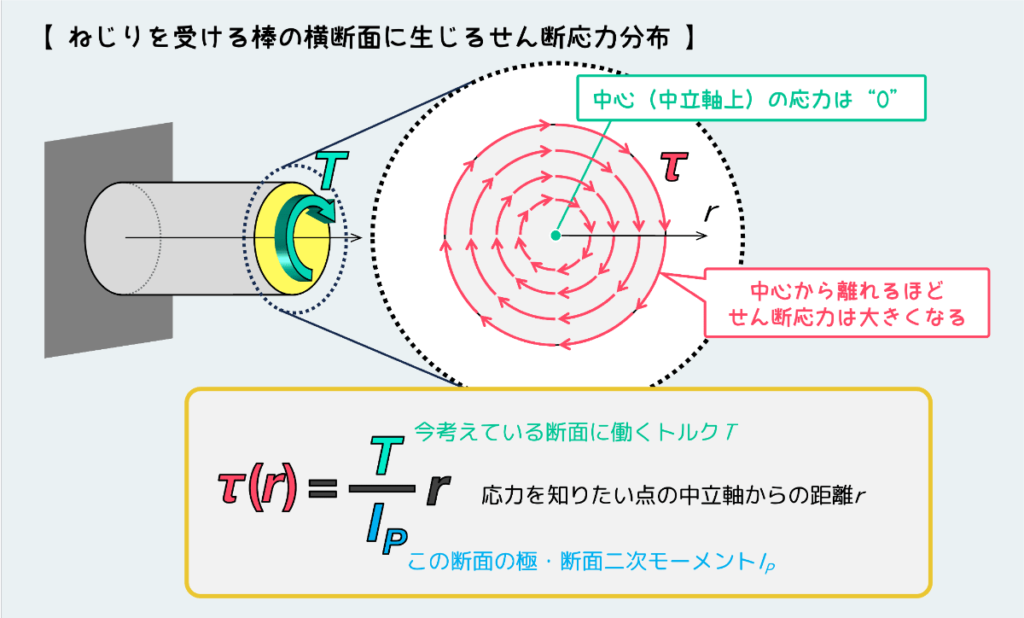
ねじりの場合は、上でも説明した通り少し特殊な形になります。しっかり押さえておきたいのは、ねじりにおいて『問題となる内力はねじりモーメントである』こと、そして『せん断応力は中立軸（中心）から離れるほど大きくなるような分布をもつ』ことです。
細かくは別の記事で説明しますが、以下に示すような公式でねじりを受ける材料の断面に生じるせん断応力を求めることができます。ここで、IPは断面二次極モーメントと呼ばれる、断面形状による変形のしにくさを表すパラメータです。
もしこのケースにおける最大せん断応力が知りたければ、この式のr のところに最大値である断面半径（d /2）を代入することで求まります。
関連する記事
さらに詳しく関連する内容について学習したい人は以下の記事を読んでみてください。
ピンやリベットが受けるせん断応力の求め方、計算方法をしっかり解説【材力Vol. 4-1】
材料力学 ねじり（トルク）によるせん断応力の考え方【材力Vol. 4-2】
【3分で解説】垂直応力とは？記号・単位・求め方を簡単解説
材料力学 応力とは？10分で完全に理解できる 基本かつ超重要な解説【材力 Vol. 2-1】
研究者を志す者 必読！！
全8巻完結
こんなにも知的探究心を刺激される漫画があったとは！
真理のために命をかけた先人たちの物語。
この作品は、現役研究者である私・ぽるこが衝撃を受けた作品として、特に研究者およびこれを志す者には強く本気でオススメします。今ある常識を疑う心、誰に何を言われようと真理を追求する姿勢に触れ、心が動くこと間違いありません。
私自身、世界のトップ研究者だった師匠によく言われた言葉を思い出します。“目の前の現象に楽な答えを持ち出し、疑うことをやめ、真理の追求という困難な道から逃げていないか！？”
本作はこういった研究者の気概なるものを感じる、必読の価値ある一冊です。全8巻ですでに完結していますし比較的手軽に一気読みできます。気になる人はぜひ読んでみてください。
私・ぽるこが全力でオススメする極上の漫画たちを紹介した記事です。思わず読みたくなる漫画が見つかるかも！
